考虑工人数量配置优化的柔性作业车间调度问题研究

梁向檩 宋豫川 雷 琦 孙爱红

重庆大学机械传动国家重点实验室,重庆,400044

0 引言

制造业是立国之本、兴国之器、强国之基。我国的制造业发展已经迈入了由中国制造到中国智造的阶段。随着个性化生产的需求增加,多品种、小批量生产的产值大约占到了机械工业总产值的80%[1]。提高生产的柔性是企业应对动态多变的市场需求的有效方式,因此,柔性作业车间调度受到了学者们的广泛关注。尽管制造业的发展方向是设备全自动化生产,但就目前而言,工人在制造过程中仍不可或缺。此外,制造行业竞争激烈,人工成本也快速上升,成本的控制对于提升企业的竞争力至关重要。在此背景下,从降低成本的角度,确定参与制造任务的不同技术水平工人的数量及最优的生产调度方案,对制造企业的发展具有重大的实际意义。

柔性作业车间调度问题(flexible job-shop scheduling problem,FJSP)在作业车间调度问题的基础上增加了机器选择的柔性。工人在实际生产中也是重要的资源,同时考虑机器与工人资源的柔性作业车间调度问题被称为双资源柔性作业车间调度问题(dual resource constrained flexible job-shop scheduling problem,DRCFJSP)。郭鹏等[2]以最小完工时间为目标,考虑工人的操作效率差异,采用基于工序排序、机器选择、工人指派三层编码的Jaya算法进行求解。董海等[3]同时考虑多能工和并行工序顺序柔性,以最大完工时间、总能耗、工人总加工时长方差最小为目标,设计了四段编码的离散回溯搜索算法进行求解。MENG等[4]在DRCFJSP中考虑了能耗目标,并采用了通过开关机减少能耗的策略。张洪亮等[5]从交货期、节能的角度,设计了一种基于三阶段解码方式的改进NSGA-Ⅱ算法对DRCFJSP进行优化。孙爱红等[6]不仅考虑了工人操作效率的异质性,还考虑了工人操作合格率的异质性,并将机床分为普通机床与数控机床,以完工时间和加工质量为目标,设计了一种两级嵌套蚁群算法进行优化。TAN等[7]研究了具有工人疲劳意识的DRCFJSP,以最小化最大完工时间和最大工人疲劳值为目标,通过改进的NSGA-Ⅱ算法求解。周亚勤等[8]在DRCFJSP的基础上,考虑关键工序需要特定设备和人员的约束,并将关键设备利用率纳入了优化目标。PENG等[9]研究了包括工件运输时间和工人学习效应约束的DRCFJSP,并提出了一种多目标帝国竞争算法进行求解。综上可知,国内外已有部分学者在DRCFJSP上进行了扩展,包括考虑节能、工人疲劳、学习效应、工件质量等。但据笔者所知,有关DRCFJSP的研究几乎均假定工人的数量是确定的,目前几乎没有相关文献考虑不同的工人数量配置方案对调度结果的影响。

制造企业本质上是以盈利为目的的生产经营组织,在保质保量的前提下降低成本是制造企业的现实目标。目前,已有一些学者基于成本的视角考虑在FJSP及其扩展模型的目标函数中加入成本指标。朱伟等[10]考虑只与机器选择有关的加工成本,设计了一种改进遗传算法求解带有工件移动时间的FJSP。刘彩洁等[11]建立了分时电价下的FJSP模型,并在目标函数中考虑了能耗成本,采用动态控制参数的NSGA-Ⅱ算法进行优化。WU等[12]将提前/拖期惩罚成本考虑至FJSP中,并通过基于3D析取图的混合蚁群算法进行求解。ZHENG等[13]研究了允许工序重叠的FJSP,以工序重叠成本和最大完工时间为目标进行了优化。李佳路[14]在研究分布式FJSP时,考虑了原料到工厂、工厂内部、工厂到成品仓库的运输成本,并设计了多种群人工蜂群算法求解。肖华军[15]在求解多目标的DRCFJSP时考虑了总成本,包括工人加工成本与机床成本。由上述文献可以看出,国内外学者在研究FJSP相关问题时已从工件、机器、工人等角度考虑了成本因素,但极少有学者同时考虑拖期惩罚成本与工人成本,并且考虑工人成本的文献基本上只考虑了工人的加工成本,而现实生活中,工人的工资大多以基础工资加绩效工资的形式构成。

综上所述,在DRCFJSP中几乎没有学者考虑工人的数量配置优化,并且在考虑工人成本时,几乎没有学者从符合实际的基础工资加绩效工资的角度考虑,因此,本文在DRCFJSP的基础上考虑不同技术水平工人的数量配置优化,建立了以最小化总成本为目标的混合整数规划模型,其中,总成本包括拖期惩罚成本和基础工资加绩效工资形式的工人成本。此外,虽然已有学者运用教学优化算法求解车间调度问题[16-18],但少有学者将其运用在DRCFJSP中。鉴于此,本文设计了一种改进的教学优化(improved teaching-learning-based optimization,ITLBO)算法对研究对象进行求解,决策出各种技术水平工人的最优数量及工人、设备资源约束下的最优生产调度方案,以实现总成本最小化地完成制造任务。通过对不同规模的10组算例进行测试,并与流行的遗传算法(GA)、粒子群优化(PSO)算法对比,验证了本文所提出的ITLBO算法的可行性与有效性。

1 问题描述及数学模型

1.1 问题描述

柔性作业车间中存在m(M1,M2,…,Mm)台机器,有w(W1,W2,…,Ww)名工人可进行作业,工人的技术水平可分为k(K1,K2,…,Kk)种,如:初级、中级、高级,假设同一技术水平的工人无差异,不同技术水平的工人存在差异,现需对n(J1,J2,…,Jn)个工件进行生产,每个工件Ji包含vi(i=1,2,…,n)道工序。加工每道工序Oij(i=1,2,…,n;j=1,2,…,vi)的可选机器集合为Mij,Mij⊆M,操作机器q(q∈Mij)完成工序Oij加工的可选工人所属技术水平集合为Kijq,Kijq⊆K,选择不同的机器、不同技术水平的工人加工工序Oij的加工时间不同。此外,不同技术水平工人的成本也不同。考虑工人数量配置优化的DRCFJSP是在同时满足工序约束、机器约束、工人约束的前提下,确定最优工人数量配置方案(即各技术水平工人的实际数量),并为各道工序确定最优机器与工人组合以及最优开工时间。本文的目标为最小化总成本,包括拖期惩罚成本和工人成本,其中,工人成本由基础工资成本与绩效工资成本组成。为了简化问题,本文给出了如下假设:①所有工件均在零时刻已经到达,所有机器与工人也均在零时刻准备就绪;②每个工件均需严格按照工艺顺序进行加工,不同工件间的加工顺序没有约束;③机器可加工不止一道工序,工人也可操作不止一台机器;④同一时刻下,一台机器只能加工一道工序,工人也只能操作一台机器;⑤各工件之间无优先级,且加工过程中不允许抢占;⑥准备时间、移动时间包含在加工时间中,可忽略不计;⑦各个技术水平的工人数量有上限,即某一技术水平的工人数量不能超过给定的最大值;⑧工序在不同机器上加工的成本差异相比于不同调度方案引起的拖期惩罚成本差异、工人成本差异较小,可忽略。

1.2 数学模型

本文在普通DRCFJSP数学模型[2,6,15]的基础上,新增不同技术水平工人的具体数量为决策变量,并设置目标函数为总成本,包括工件拖期惩罚成本、基础工资加绩效工资形式的工人成本。为清晰地表述所构建的数学模型,本文涉及的符号及含义如表1所示。

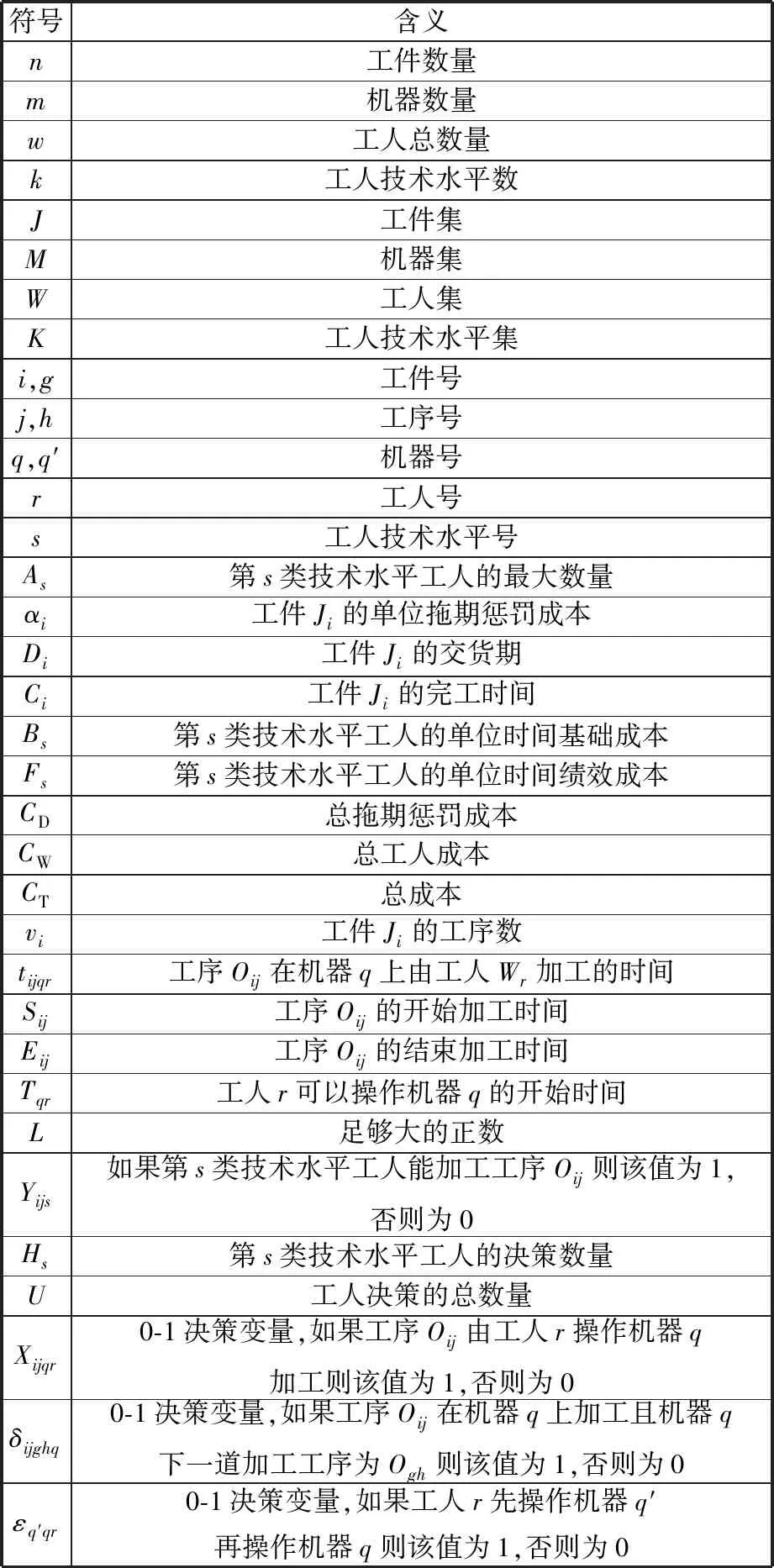
表1 符号及含义

基于本文给出的假设及表1中的符号变量,建立的数学模型如下:

f=min(CT)

(1)

CT=CD+CW

(2)

(3)

(4)

约束条件如下:

(5)

(6)

Tqr+L(Xijqr-1)≤Sij

(7)

Sgh+L(1-δijghq)≥Eij

(8)

Tqr+L(1-εq′qr)≥Tq′r

(9)

(10)

0≤Hs≤As

(11)

(12)

(13)

Sij≥0Tqr≥0tijqr≥0

(14)

其中,式(1)表示优化目标为最小化总成本;式(2)～式(4)分别表示车间调度的总成本、拖期惩罚成本、工人成本;式(5)表示工序的加工不允许抢占;式(6)表示同一工件的各工序间存在先后顺序约束;式(7)表示每道工序均需在对应的机器和工人准备好后才能开工;式(8)和式(9)表示同一时刻下工人只能操作一台机器对工序进行加工;式(10)表示每道工序只能选择一台机器和一名工人进行加工;式(11)表示每种技术水平工人的决策数量应不超过给定的最大数量;式(12)表示工人的决策总数量为各种技术水平工人的决策数量之和;式(13)表示对于任意一道工序,至少有一名工人满足加工条件;式(14)表示零时刻时,工件已经全部到达,工人、机器全部准备就绪,加工时间大于0。

2 改进教学优化算法设计

2.1 算法总体流程

教学优化(TLBO)算法是RAO等[19-20]基于模拟教学过程提出的一种群体智能优化算法,进化原理为教师解引导学生解向最优解所在的空间收敛以及学生解之间相互学习以避免算法快速陷入局部最优。传统TLBO算法适用于连续型问题的求解,且在局部搜索能力、保持种群多样性方面存在不足。针对本文研究问题的特点,对传统TLBO算法进行改进,采用基于工人数量配置、工序排序、机器选择的三层编码方案。教师阶段采用变邻域搜索(variable neighborhood search,VNS)算法进行教师自学。学生阶段以概率选择向老师学习或向其他学生学习,并以Metropolis准则判断是否接受新解。此外,学生小概率地进行自学。

本文设计的ITLBO算法总体流程如图1所示,算法的具体步骤如下:

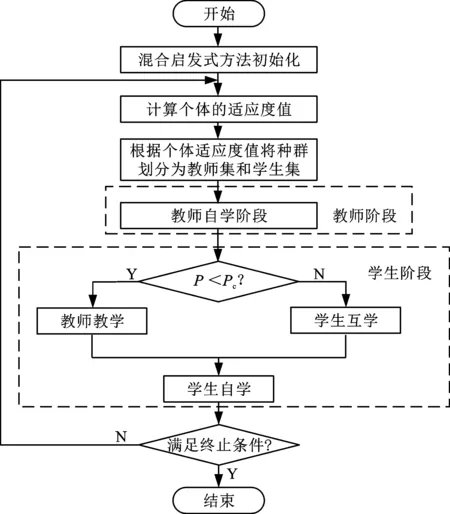
图1 改进教学优化算法流程图

(1)根据设置的种群规模,采用混合启发式方法初始化种群。

(2)对种群个体进行解码,得到每个个体的适应度值。由于调度目标为总成本最小,因此,适应度值取总成本的相反数。

(3)将个体按照适应度值降序排序,根据教师解占比系数a%,取前a%的个体作为教师解,其余个体为学生解。

(4)教师自学。采用VNS算法对教师解进行局部搜索。

(5)学生向他人学习。对于每个学生,产生一个0-1的随机数P,若P小于设定的学习方式概率系数Pc,则任选一名教师对该学生进行教学;否则,该学生任选一名同学互相学习。两种向他人学习的方式均通过交叉算子来实现,并以Metropolis准则判断是否接受新解。

(6)学生自学。对于每个学生,产生一个0-1的随机数P,若P小于设定的学生自学概率系数Pm,则通过变异算子来实现该学生的自学。

(7)判断是否满足终止条件,若满足,则结束循环并输出最优解;否则,跳转至步骤(2)。其中,小规模算例收敛速度快,终止条件选择为最大迭代次数;大规模算例可能收敛速度较慢,终止条件选择为最大最优解不变次数。

2.2 编码与解码

考虑工人数量配置优化的DRCFJSP模型,需要同时解决工人数量配置、工序排序、机器选择、工人选择四个子问题。目前,学者们在解决车间调度问题时,采取的编码方式可分为两类:全解空间编码、部分解空间编码。全解空间编码虽能实现在整个解空间内搜索,但对于解空间极大的模型,算法的效果通常不理想。相反,采用部分解空间编码容易保证算法的收敛性与稳定性[21]。因此,为了综合考虑算法的搜索空间与收敛性,本文采用基于工人数量配置(WNA)、工序排序(OS)、机器选择(MS)的三层部分解空间编码。图2展示了一个编码实例,WNA行的长度等于工人技术水平数,从左往右指代的工人技术水平由低到高,各数字表示相应技术水平工人的数量;OS行的长度等于总工序数,各数字表示工件号,各数字出现的次数表示工序号;MS行的长度等于总工序数,从左往右依次指代J1至Jn的相应工序,各数字表示相应工序可选机器集中的顺序号,而非机器号。

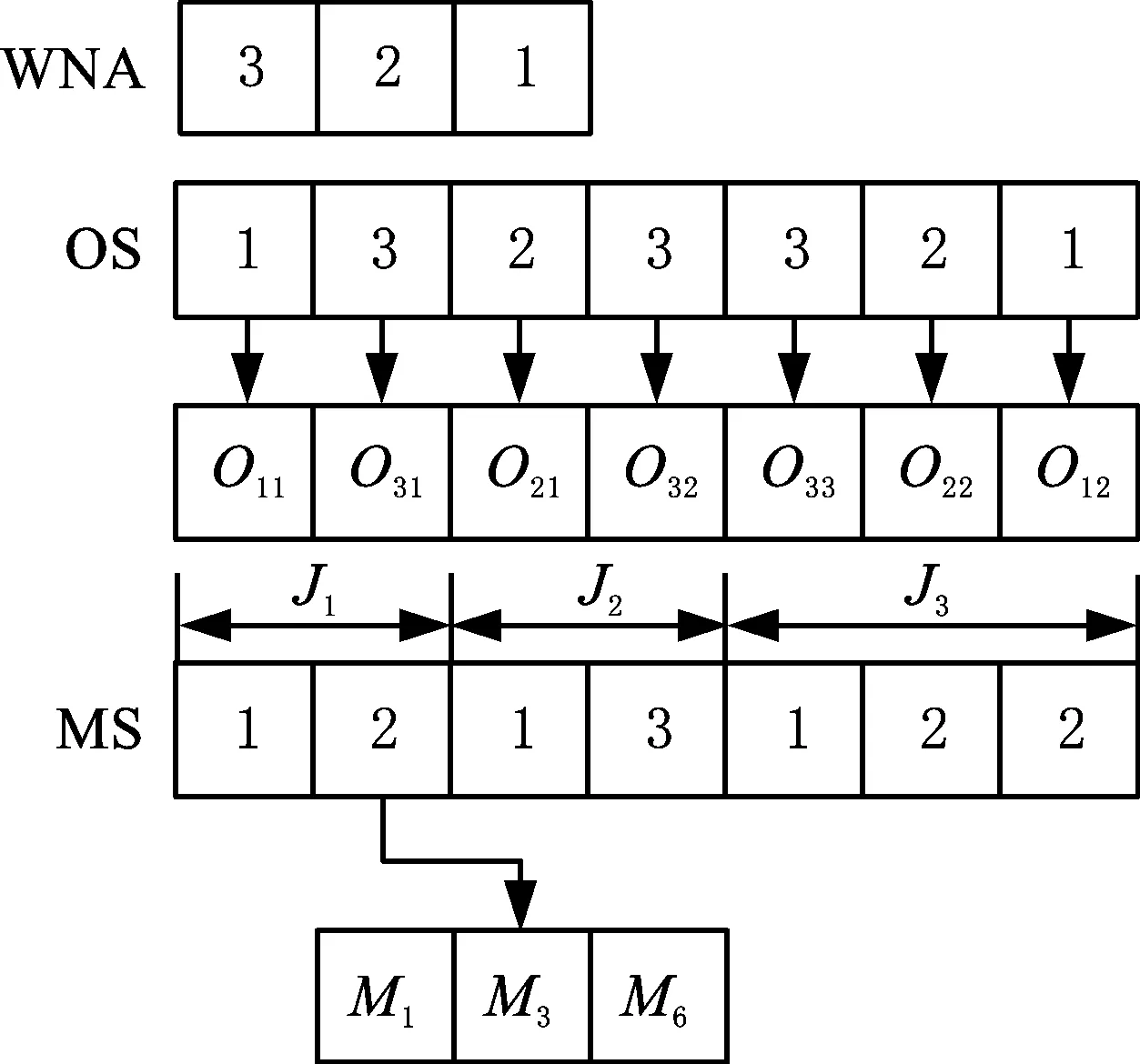
图2 编码实例

编码中未涉及的工人选择通过在解码过程中使用启发式规则确定。考虑到问题的优化目标,采用插入式贪婪解码以获得活动调度。考虑工人数量优化配置的DRCFJSP的解码流程如图3所示,具体的解码步骤如下:

图3 解码流程图

(1)通过WNA编码获取各技术水平工人的数量,从左往右依次读取MS编码以获取机器选择矩阵。其中,机器选择矩阵各元素表示各工序选择的机器号,而非可选机器集中的顺序号。

(2)对WNA编码进行可行性检查,若存在某道工序可选工人集为空集,则随机选择一种可加工该工序的工人类型,令该类型的技术水平工人数为1,直至满足所有工序的加工要求。

(3)对修正数量后的所有工人进行编号,按照技术水平由低到高的顺序依次令工人编号为1,2,…,U。

(4)从左往右依次读取OS编码,结合机器选择矩阵得到工序的加工机器号与可选加工工人集。采用间隙挤压法确定各可选加工工人最早完成工序加工的时间,选择完成时间最早的工人加工此工序,若最早能完成的工人不唯一,则选择其中工人编号最小的工人以降低工人绩效成本。

(5)检查所有工人的加工时间表,若存在某名工人的加工时间表为空(即该工人未加工任何工序),则将WNA编码中对应的技术水平的工人数减1,直至遍历完所有工人。

(6)按照式(2)～式(4)计算总成本。

本文所设计的解码方法既考虑了尽早完工以降低拖期惩罚成本和工人基础成本,又在保证尽早完工的同时考虑了选择技术水平较低的工人以降低工人绩效成本。通过选择最早完工的工人还可达到均衡工人负荷、识别劳动力过剩的效果。

2.3 初始化

由于本文研究的问题是FJSP的扩展,算法的搜索空间更为庞大,因此初始解的质量对TLBO算法求解的质量和速度起着非常关键的作用。张国辉[22]从机器负荷尽可能平衡的角度出发,针对机器选择提出了一种全局选择(GS)、局部选择(LS)、随机选择(RS)相结合的初始化方法。赵诗奎等[23]在机器选择初始化时,不考虑工序的顺序约束,从最小化极限调度完工时间的角度,提出了改进全局选择(IGS)、改进局部选择(ILS)、RS相结合的初始化方法。针对本文的编码特性,WNA和OS部分采用随机初始化方法,MS部分采用GS、IGS、LS、ILS、RS相结合的混合初始化方法。由于初始化阶段并未指定工序的工人选择,因此在MS部分初始化时,工序在指定机器上的加工时间由可选工人加工时间的平均值代替。结合文献[22-23]的建议及实验测试,最终选定GS、IGS、LS、ILS、RS各自的占比分别为0.3、0.3、0.15、0.15、0.1。

2.4 教师阶段

标准TLBO算法设置一个全局最优解为教师,这种设置方式可能会导致种群的平均适应度值增大缓慢且种群多样性过早丢失。为克服此弱点,本文在整个群体中选择最优的前a%个个体作为教师。由于教师解的质量较高,采用全局搜索不利于探索到更高质量的解,因此,通过变邻域搜索实现教师的自学。邻域结构的设计是变邻域搜索的关键。基于工人基础成本、拖期惩罚成本与时间指标密切相关,对关键路径上的关键工序进行扰动有利于缩短完工时间,因此,本文以关键工序为对象设计邻域结构。

关键路径是指满足工序顺序约束的条件下获得的最长加工路径,关键路径中包含的工序即为关键工序。针对本文所研究问题的特点,设计了如下两种邻域结构:

(1)邻域结构一。随机选择两道不属于同一工件的工序,其中至少一道工序为关键工序,交换这两道工序,但不改变工序的加工机器。

(2)邻域结构二。随机选择一道关键工序,将其加工机器更换为其他可选机器。

需注意的是,关键路径可能不止一条,考虑到尽可能优化总成本,本文选择从后往前搜寻的方式确定出一条关键路径进行局部搜索。具体步骤如下:

(1)找到最后完工的工序,若不止一个,则选择所属工件拖期惩罚成本最高的工序作为临时工序,并放入关键路径。

(2)判断临时工序的同一工件紧前工序的完成时间是否与临时工序的开始时间相同,若相同,则将其同一工件紧前工序作为临时工序,并放入关键工序;否则,按照同样的方法依次判断临时工序的同一机器紧前工序、同一工人紧前工序。

(3)判断临时工序的开始时间是否为0,若为0,则结束;否则,跳转至步骤(2)。

2.5 学生阶段

本文所设计的学生阶段的学习方式可分为向他人学习与自学两种。在向他人学习时,标准TLBO算法既包括教师教学,又包括学生互学,但考虑到本文算法在教师阶段已增加了局部搜索算法,为了减少算法整体的计算时间,本文算法设计为当一名学生向他人学习时,以Pc的概率选择任意一名教师教学,否则选择任意一名同学互相学习。为了保证算法的收敛速度,学生解应更高概率地选择教师教学,因此,Pc的取值应大于0.5。考虑到离散问题的特性,本文选用交叉算子实现向他人学习,其中,WNA、MS编码采用均匀交叉(UX),OS编码采用基于工件优先顺序的交叉(POX),如图4所示。

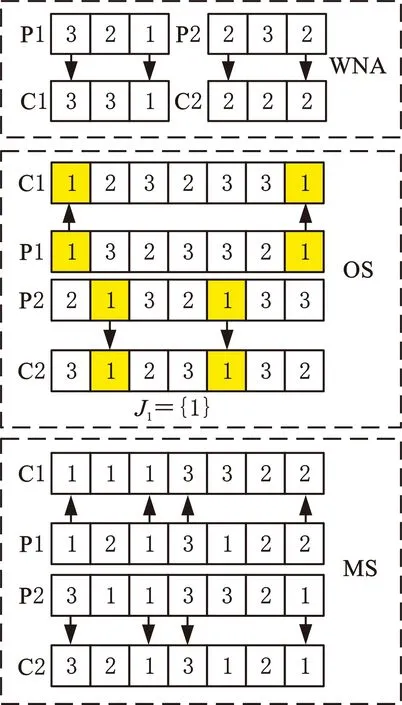
图4 学生向他人学习算子

标准TLBO算法在教师教学、学生互学后会保留适应度更高的解,虽然此方法可以保证更优的个体进入下一代,但也容易导致算法陷入局部最优。为了克服这一缺陷,本文选择交叉后适应度高的个体作为临时个体,以Metropolis准则判断是否接受临时个体,Metropolis准则的计算表达式如下:

(15)

式中,df为临时个体与原始学生目标函数值的差值;kB为温度衰减系数,本文取kB=0.9;T0为初始温度,考虑到不同算例的df数量级可能存在较大差异,本文将T0取为初代群体中最大目标值差(即最大目标值与最小目标值的差值)的10倍。

学生完成向他人学习后,以Pm的概率进行自学,本文选用变异算子实现学生自学,其中,对于WNA、MS编码,随机选中l个位置,将其编码随机更改为可选范围内的其他值,OS编码采用插入变异,如图5所示。

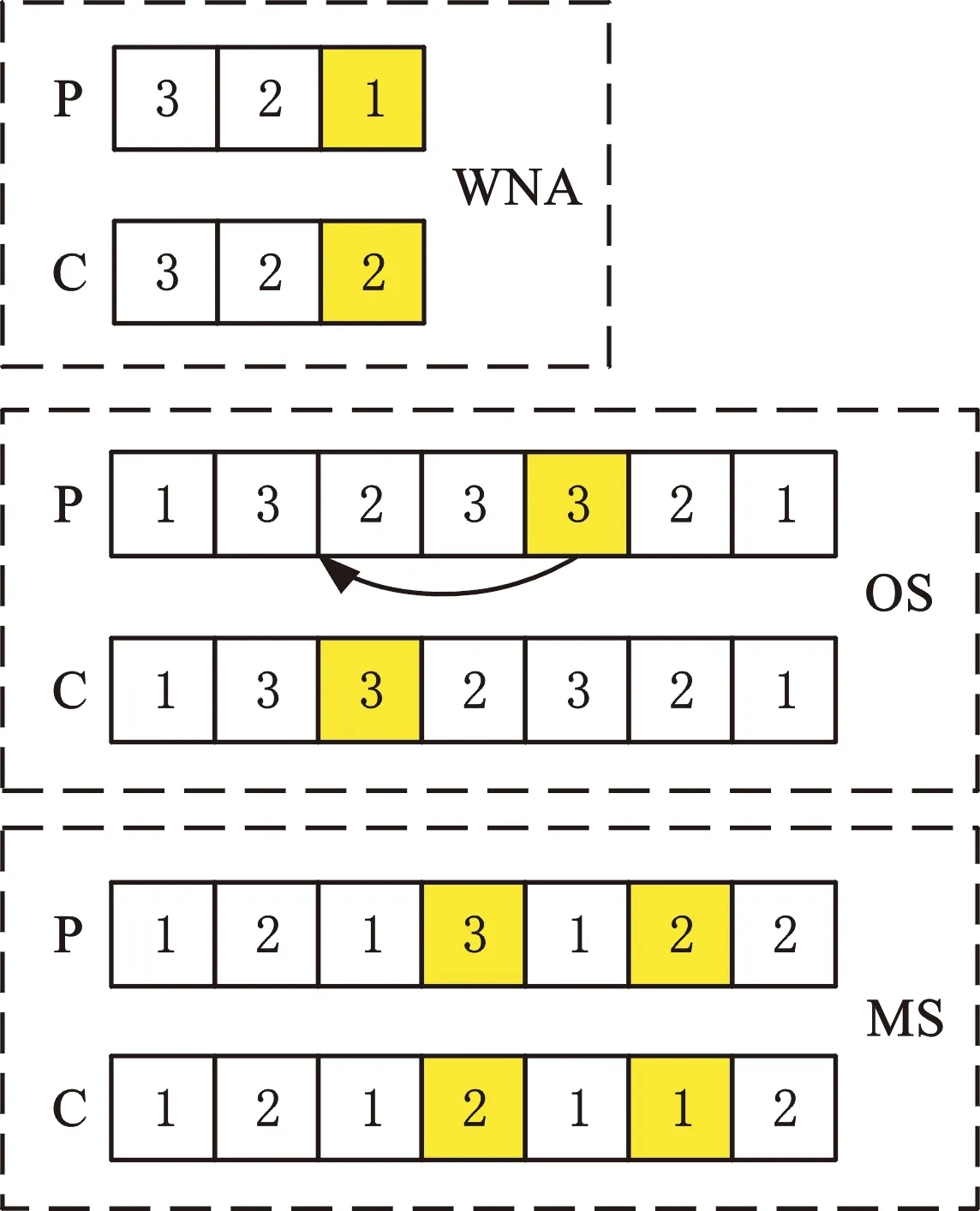
图5 学生自学算子

3 实验分析

本文所有测试均由Python3.7实现,计算机硬件配置为英特尔i7-7700HQ CPU(2.8 GHz)、8 GB RAM,操作系统为Windows 10。

3.1 测试算例

由于目前尚未有考虑工人数量配置优化的DRCFJSP算例,因此本文基于文献[15]中的算例进行设计。文献[15]中的算例考虑工人数量一定且各工人技术水平皆不相同,工人成本方面只考虑了工人加工成本。基于此,本文将文献[15]算例中的工人加工时间数据整合为2或3种技术水平工人的加工时间数据,具体为:将加工成本相近的多名工人的加工时间采用求平均值的方式整合为一种技术水平工人的加工时间。各种技术水平工人的基本成本、绩效成本在[10,70]范围内随机生成,且满足技术水平高的工人的成本更高。各种技术水平工人的最大数量在[2,5]范围内随机生成,结合实际,考虑为技术水平较低的工人的最大数量相对较多。工件的交货期采用下式计算:

(16)

其中,Zi为工件Ji的紧迫系数,在[1,1.5]范围内随机生成;tij为可用的机器和工人组合加工工序Oij的时间平均值。工件的单位拖期惩罚成本在[5,40]范围内随机生成。最终,本文生成了10个测试算例,命名为DSP-WN01-10,测试算例的详细数据可扫描本文首页OSID二维码获取。

3.2 算法参数

本文提出的ITLBO算法除了前文中已经确定的参数设定外,还需确定种群规模N、教师解占比系数a%、学习方式概率系数Pc、学生自学概率系数Pm、最大迭代次数或最大最优解不变次数Gt。若种群规模太小,会导致初始解的分布密度过低且多样性较差,不利于对整个解空间的搜索;若种群规模太大,会导致算法运行时间明显增加[24],因此,本文对小规模算例设定种群规模为100,对大规模算例设定种群规模为300。针对算法终止条件,考虑到随着算例规模的增大,算法的收敛速度通常是降低的,本文对小规模算例设定最大迭代次数为100,对大规模算例设定最大最优解不变次数为100。剩余的三个参数通过正交试验确定最优的参数组合,每个参数选择3个水平,如表2所示。选择L9(33)正交表进行试验,算例选择改编的DSP-WN02,取算法运行10次的平均总成本(average total cost,ATC)作为各种参数组合下的评价指标,计算结果如表3所示。

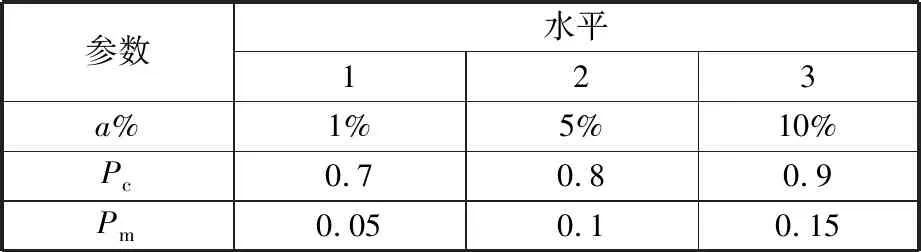
表2 参数水平表

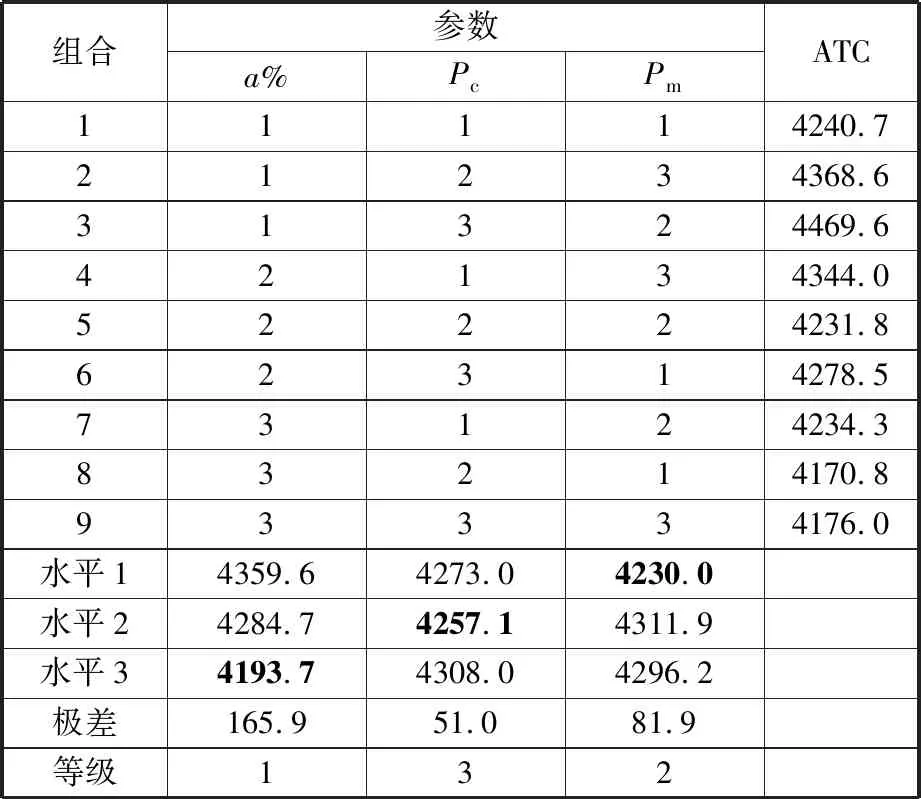
表3 正交试验表

根据表3结果绘制参数水平趋势图(图6),可以看出,当a%、Pc、Pm分别取第三水平、第二水平、第一水平时,ATC最小,因此,本文最终设定a%=10%,Pc=0.8,Pm=0.05。

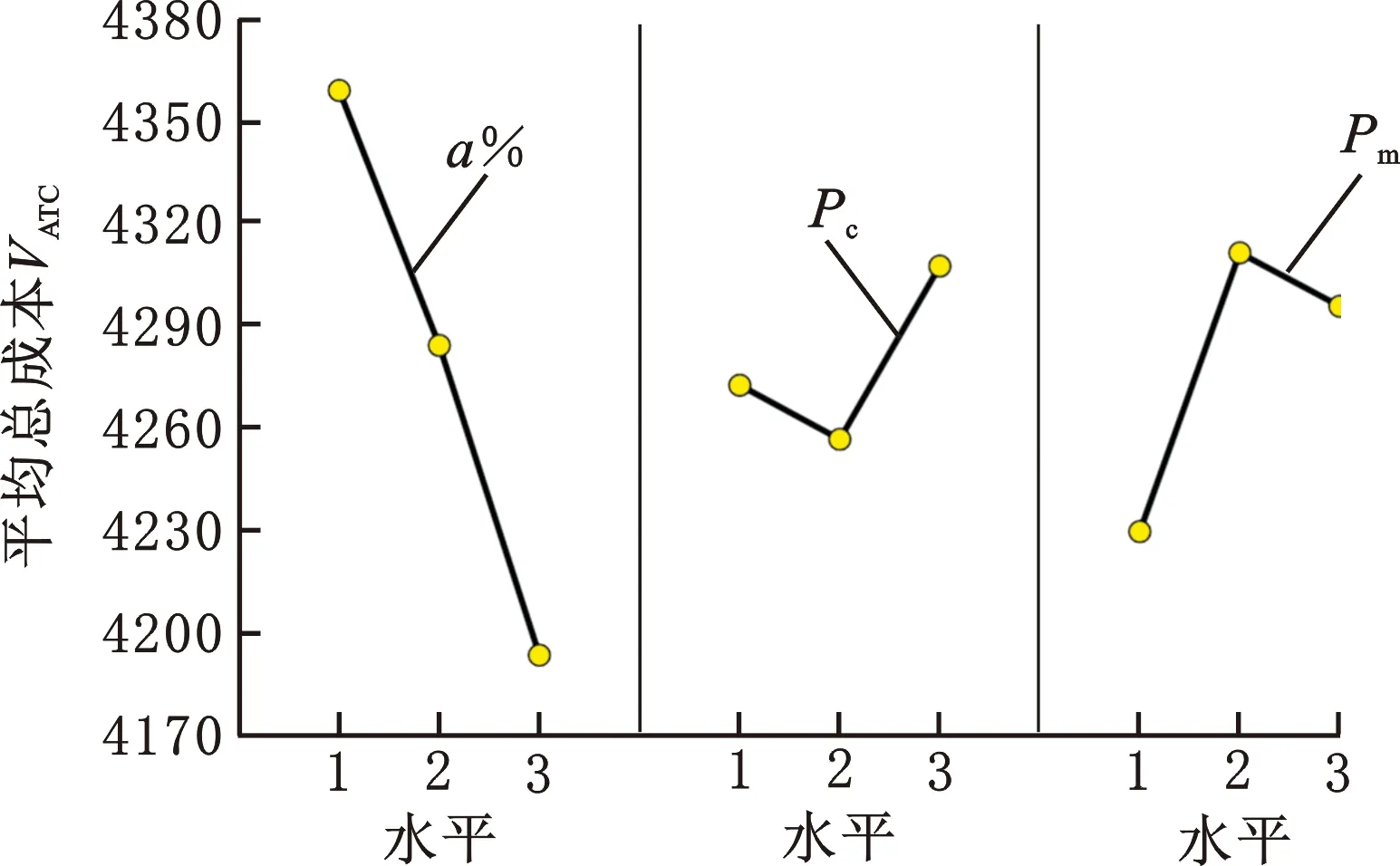
图6 参数水平趋势图

3.3 邻域结构有效性测试

为验证所设计邻域结构的有效性,在初始化方法、学生阶段及算法参数保持不变的基础上,将教师阶段中变邻域搜索的邻域结构替换为图5中OS、MS的变异算子,为描述方便,将此算法命名为NTLBO。将NTLBO和ITLBO两种算法在3.1节生成的DSP-WN01-10算例中进行对比测试,对于每个算例,每种算法独立运行10次,测试结果如表4所示。表4中加粗的部分表示更优,其中,最优工人配置表示各种技术水平工人的数量,从左往右工人的技术水平依次提高,如(3,0,1)表示工人的技术水平总共有3种,其中,初级工3人,中级工0人,高级工1人。测试结果表明,两种算法仅在DSP-WN01小规模算例上的求解性能持平,在其余的9个测试算例中ITLBO算法取得的最优解与平均值更好。这表明本文设计的邻域结构能有效地增强算法的局部搜索能力,并提高算法搜索更优解的概率。

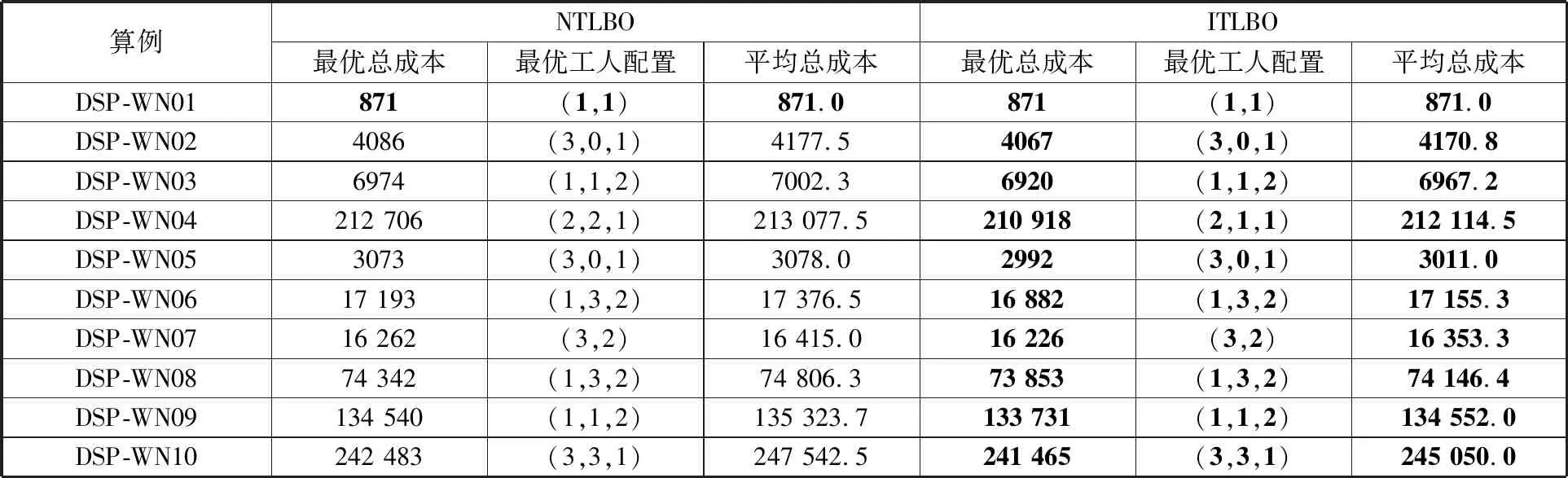
表4 邻域结构有效性测试结果

3.4 与其他算法对比测试

为进一步验证本文所提算法的优越性,同时验证所设计的编解码方法、进化算子应用于不同算法框架的有效性,采用遗传算法(GA)、粒子群优化(PSO)算法作为对比算法,对3.1节生成的DSP-WN01-10算例进行测试。对于每个算例,每种算法独立运行10次,各算法决策出不同技术水平工人的最优数量配置及总成本最低的生产调度方案,并对算法获取的最优解及稳定性进行分析。其中,GA、PSO算法的框架分别采用文献[22]和文献[25]所提出的框架。为了保证对比的公平性,两种对比算法的初始化均采用2.3节提出的初始化方法。对比算法的关键参数参考文献[22,25]的建议,如表5所示。三种算法所求出的最优解如表6所示。

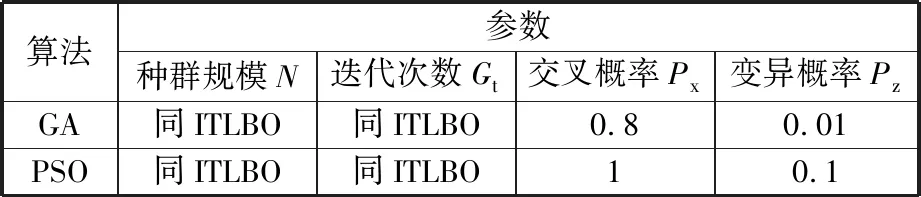
表5 对比算法参数表

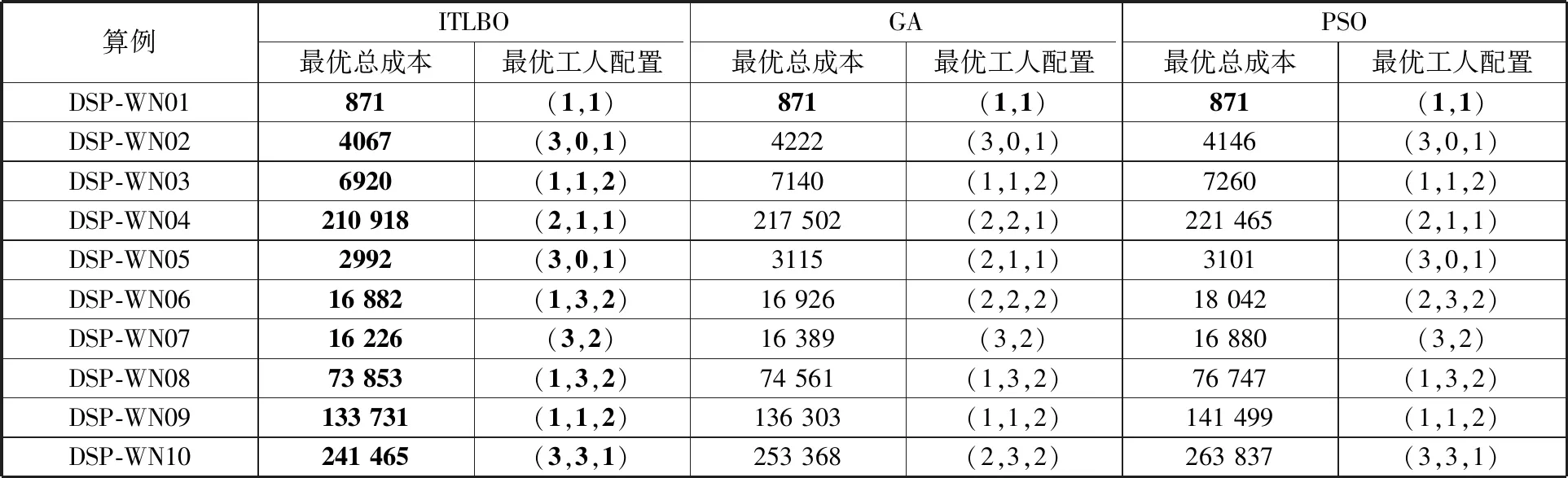
表6 三种算法所求的最优解

表6中加粗的部分为各个测试算例中获取到的最优总成本、最优工人配置。从表6中可以看出,本文所设计的编解码方法及交叉、变异算子应用于三种算法中时均能优化所建立的模型,从而验证了编解码方法及进化算子的有效性且通用于多种算法框架。此外,本文所设计的ITLBO算法在生成的10个测试算例中均获得了最佳解,其余两种算法只在最小规模算例DSP-WN01中获得了与本文所设计算法同等效果的解,这是因为DSP-WN01算例的解空间相对较小,算法的求解难度较低,而在剩余9个算例中获得的最优解的质量均低于本文所设计算法,这是因为算例的规模越大,算法搜索到最优解的难度也就越大。总之,就算法搜索最优解的性能而言,本文所设计算法明显优于对比算法。

为了避免误差的影响,且更加准确地对比三种算法的性能,本文进一步使用平均总成本(ATC)、最大总成本(maximum total cost,MTC)、总成本标准差(standard-deviation of total cost,STC)三个指标对算法性能进行分析,结果如表7所示。其中,ATC、MTC、STC分别表示算法在10次运行中获得的最优解的平均值、最大值、标准差。

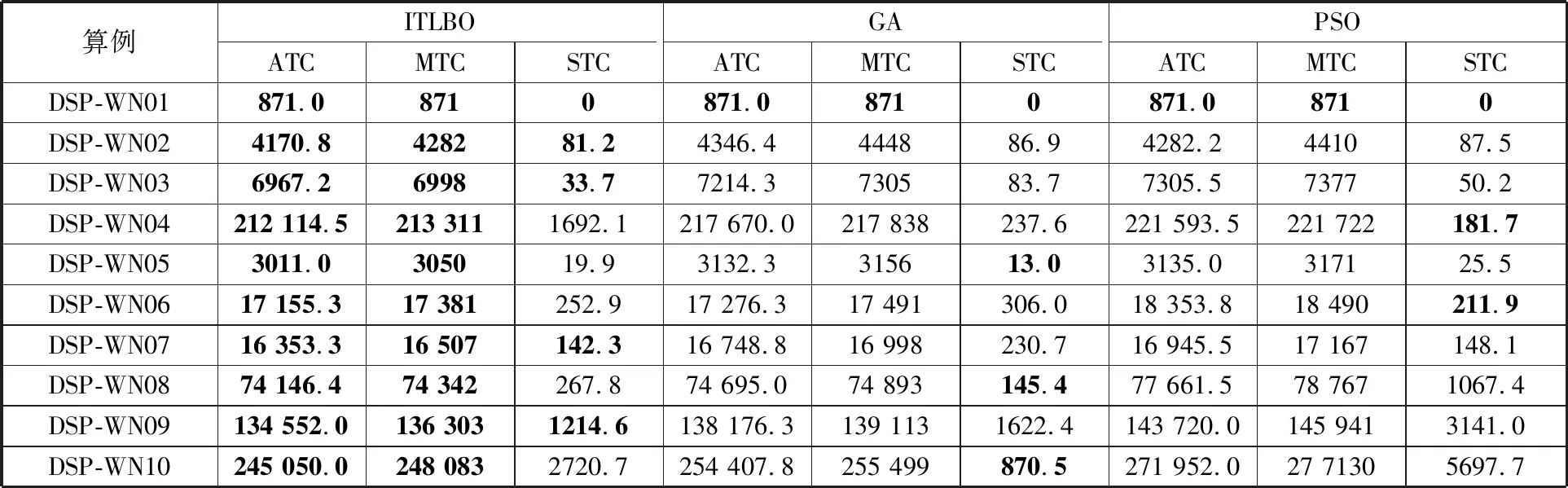
表7 三种算法的ATC、MTC、STC

表7中加粗部分为各个测试算例中ATC、MTC、STC的最优值。从表7中可以看出,本文所提的ITLBO算法在10个测试算例中ATC、MTC全部取得了3种算法中的最优值,其中,9个算例的ATC、MTC小于GA、PSO算法对应的指标值,仅在最小规模算例DSP-WN01中ITLBO算法与GA、PSO算法持平,表明相较最优解相对偏差的平均值以及悲观情况下的求解质量来看,本文所提算法存在较大优势,特别是在求解具有一定规模的算例时优势明显。就算法求解结果的标准差而言,ITLBO算法在5个测试算例的STC取得了3种算法中的最优值,其余5个算例中,也有3个算例的STC与最优值比较接近。总体而言,本文所提算法在求解考虑工人数量配置优化的DRCFJSP时性能优异且较为稳定。

为更加具体地展示3种算法在求解测试算例时的性能表现,给出了3种算法在求解小规模测试算例DSP-WN03和大规模测试算例DSP-WN10时的迭代曲线,分别见图7、图8。需注意的是,DSP-WN03算例的终止条件为迭代次数100次,DSP-WN10算例的终止条件为最大最优解不变次数100次。从图7、图8中可以看出,本文所提算法相比于GA、PSO算法,在求解小规模测试算例和大规模测试算例时,不仅取得了更优的解,并且收敛速度也更快。所提算法与对比算法在测试算例中的表现存在以上差异的主要原因可能在于所提算法嵌入了基于关键路径的局部搜索算法,并且在进化过程中并没有类似于GA中的种群选择算子,而是通过教学过程既可以向教师解学习,也可以向其他学生解学习的方式,从而保证种群的多样性。

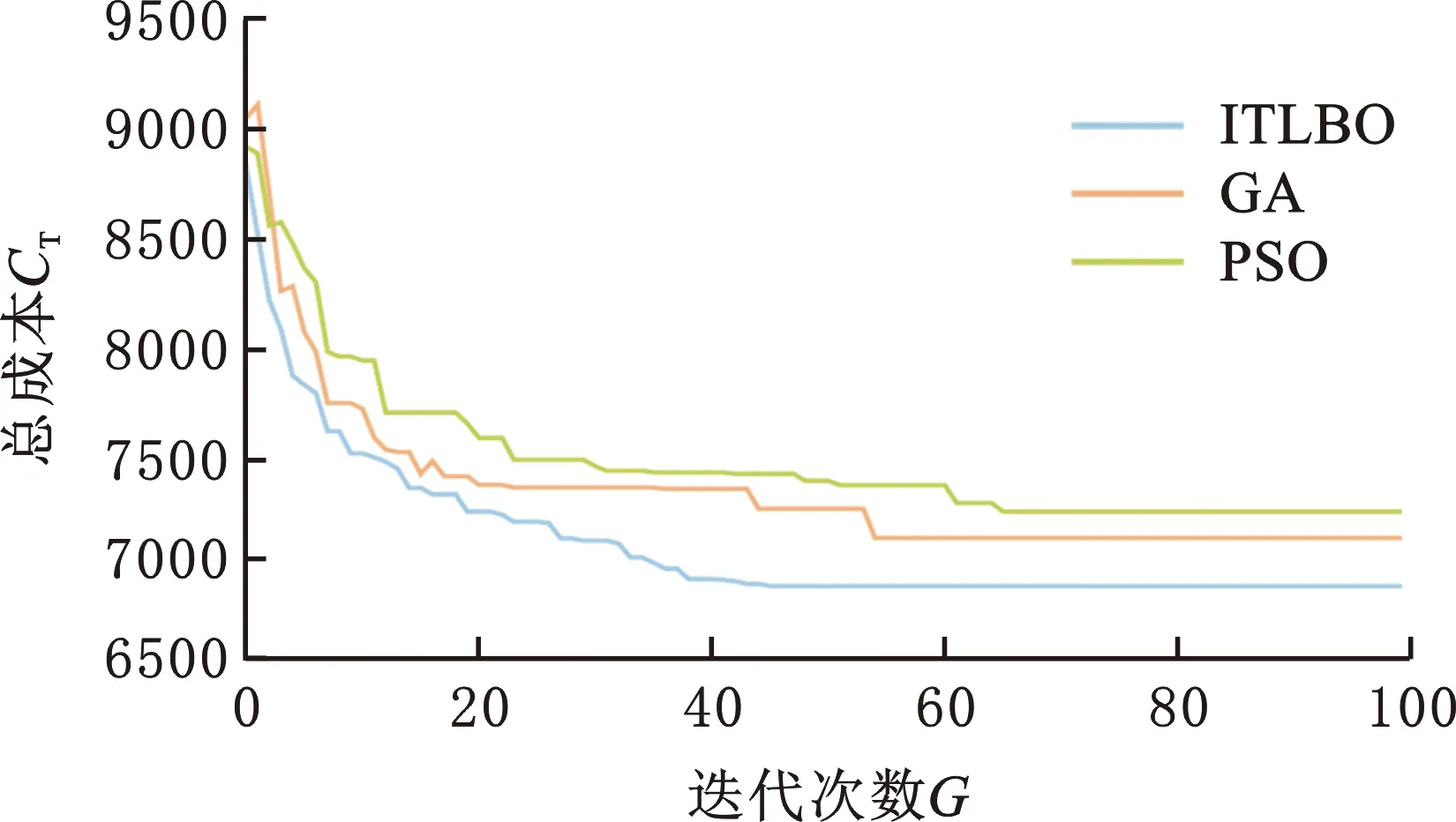
图7 DSP-WN03迭代图

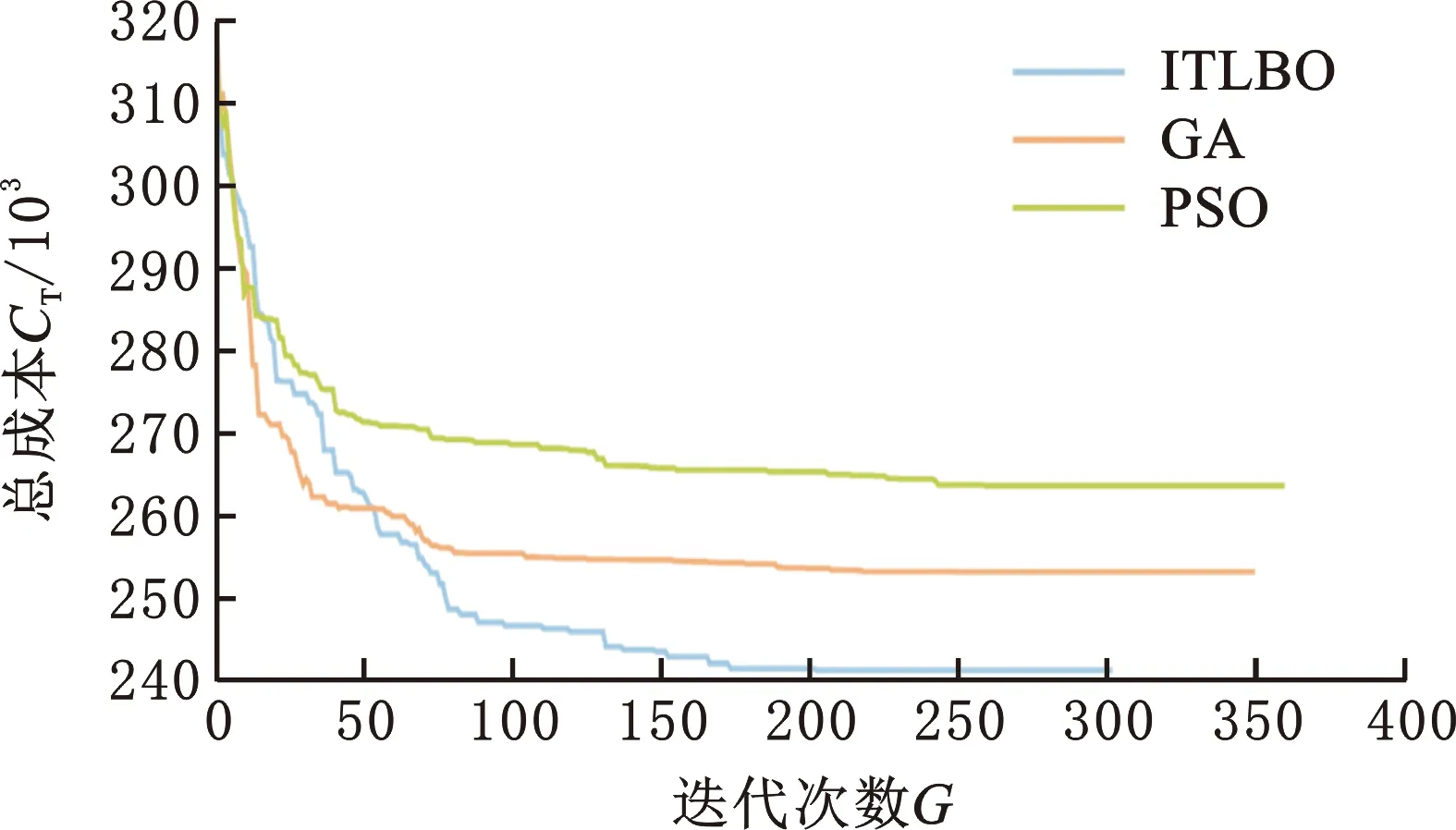
图8 DSP-WN10迭代图

图9、图10分别为所提算法在DSP-WN03、DSP-WN10测试算例中取得的最优解的调度甘特图。

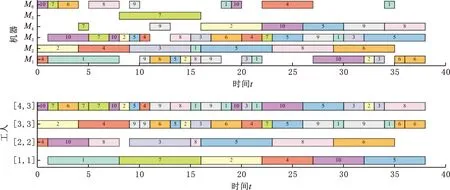
图9 DSP-WN03甘特图(总成本为6920,最大完工时间为38)

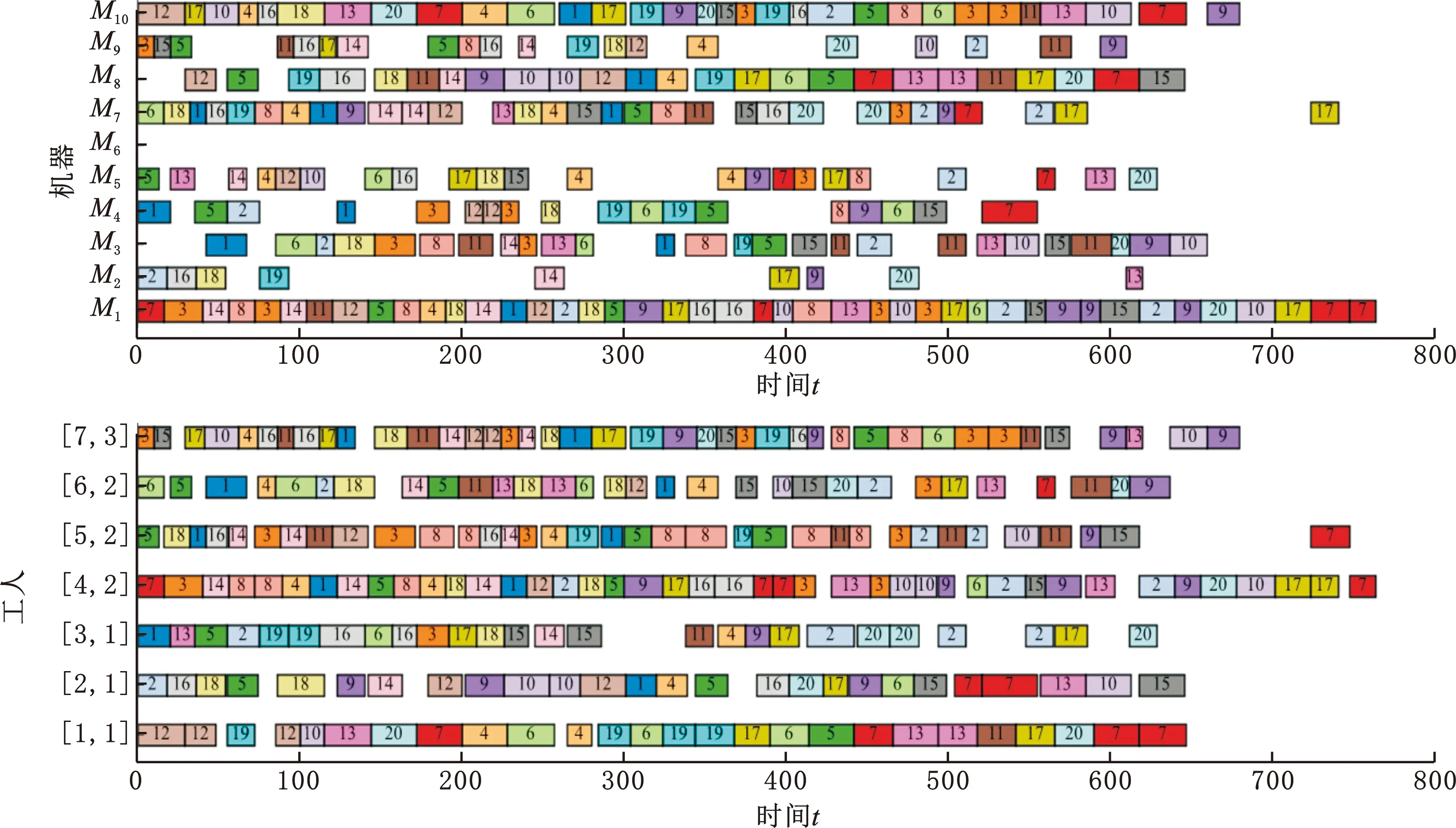
图10 DSP-WN10甘特图(总成本为241 465,最大完工时间为764)

在图9、图10中,调度甘特图的上半部分为机器调度甘特图,下半部分为工人调度甘特图,横坐标均为加工时间,纵坐标分别为机器号、工人代号,工人代号以[工人编号,工人所属技术水平号]的形式表达,如图9中的[4,3]表示第4个工人,其技术水平为第3类,即为高级工。图中方框里的数字表示工件号,从左往右依次表示该工件的加工次序,如图9中最左边的紫色方框表示工件J10的第1道工序,它在机器M6上由第4个且技术水平为第3类的工人完成加工,加工开始时间为0。

4 结论

本文针对考虑工人数量配置优化的柔性作业车间调度问题进行研究,实现了集成优化不同技术水平工人的具体数量及生产调度方案。首先,在双资源柔性作业车间调度问题(DRCFJSP)的基础上,新增不同技术水平工人的数量配置为决策变量,建立了以最小化总成本为目标的数学模型。其次,提出了一种改进的教学优化算法,该算法采用基于工人数量配置、工序排序、机器选择的三段式编码表示调度解,并基于优化目标,设计了一种结合启发式规则的贪婪插入式解码方法;初始化阶段,采用了混合启发式初始化方法;教师阶段,设计了有效的邻域结构来提高解的质量。最后,生成了适用于本文所提模型的测试算例,测试结果验证了所设计邻域结构的有效性。通过与其他算法对比,进一步验证了本文所提算法能确定不同技术水平工人的具体数量,以更低的成本完成制造任务,证明了所提算法的优越性。

本文所研究的问题在未来还有进一步的发展空间,主要包括:①由于机器、工人均对加工时间的准确性产生影响,因此在本文所提问题的基础上进一步考虑模糊生产环境对实际生产意义重大;②在本文问题的基础上,构建多目标优化模型;③构建在机器维护、工人请假等情况下的动态调度模型。