考虑加班的无拖期作业车间调度问题多目标金鹰优化算法研究

史双元 熊禾根

武汉科技大学机械自动化学院,武汉,430081

0 引言

制造系统优化调度是实现制造资源优化利用和提高生产运作效率的重要和关键技术之一。在诸多的制造系统优化调度目标中,对于面向订单型制造企业,满足客户订单的交货期是最重要的目标之一。然而,由于企业内部生产能力相对稳定与外部订单任务随机性之间的矛盾,当制造系统负荷率较高时,常规工作时间的生产作业可能导致某些订单的拖期交货,进而造成因拖期惩罚而带来的经济损失和影响企业商誉。为了尽可能避免上述不利情况的发生,企业管理者通常在采用生产优化调度的同时,通过加班作业的方式扩充常规生产能力,从而尽力保证订单无拖期交货。显然,一方面,加班作业可以扩充生产能力,但另一方面也会产生额外的生产费用。如若加班作业在时间和资源对象上安排不恰当不合理,可能不但无法有效和针对性地提前订单的完成时间,还会增加企业生产成本。如何将加班作业与优化调度进行融合,从而实现企业损失的最小化和效益的最大化,是面向订单型企业生产运作管理亟待解决的重要问题。为此,本文提出了一种考虑加班作业的多目标无拖期作业车间调度问题(multi-objective no-tardiness job shop scheduling problem with overtime consideration,MONTJSSP/O),以期通过问题的研究,在生产负荷较重但处于有限范围内的状况下,充分和优化地利用加班作业,从而实现订单的无拖期交货。

MONTJSSP/O问题的关键特征在于无拖期交货和考虑加班作业。在大量与拖期有关的作业车间调度问题研究中,绝大多数研究对问题进行数学建模时,将交货期考虑在优化的目标函数中,如最小化(加权)总拖期和/或总提前、最小化最大拖期、最小化(加权)拖期工件数量等[1-5]。这些研究只是降低了拖期程度,并不能保证订单的无拖期交付。现有研究中,在作业车间调度问题中考虑无拖期约束的研究尚未见到,与无拖期相关的调度问题研究报道也比较少,且基本是针对单机调度问题[6-8]的。CHAND等[6]针对无拖期单机调度问题,以总加权提前量为优化目标,设计了精确算法和近似方法进行求解;ZHAO等[7]分析了具有劣化作业(即工件加工时间随着开工时间线性递减)的单机调度问题,在满足无拖期工件的前提下,提出了以最小化总提前惩罚为目标的优化算法。加班作业是制造企业应对客户需求激增常采用的一种短期扩大产能的方法[9-10]。查阅已有文献发现,针对作业车间调度问题,通过加班作业扩大产能的研究不是很多。ZHANG等[11]通过加班作业提高产能,以单机调度问题研究了无拖期交付的问题。HOLLOWAY等[9]提出了一种考虑工件交货期和加班作业的静态和动态作业车间调度问题解决方法,以找出加班与总拖期之间的关系。YODA等[12]通过在每个常规班次中延长加班时间来调整产能,并以最小化总拖期和总加班时间为优化目标。上述文献或者不是基于作业车间调度问题进行的研究,或者不是真正意义上的无拖期交付。

问题求解方面,本文提出了基于精英保留策略的非支配排序金鹰优化算法(elitist non-dominated sorting golden eagle optimizer,NSGEO)。金鹰优化算法(golden eagle optimizer,GEO)是一种基于群体的新型智能优化算法[13]。自GEO算法被提出以来,已被应用于诸多领域[14-17]。针对多目标问题,MOHAMMADI-BALANI等[13]扩展单目标GEO算法提出了多目标金鹰优化算法,在10个标杆测试函数上对算法性能进行了测试和验证,结果表明所提算法的性能优于其他用于对比的常见多目标算法(包括多目标灰狼算法、带精英保留策略的非支配排序遗传算法、多目标粒子群算法、多目标樽海鞘群算法)。从上述文献中可以看出,多目标金鹰优化算法在求解多目标优化问题时能表现出较好的性能。

综上所述,本文研究的创新点主要体现在:①已有拖期相关作业车间调度问题研究主要将拖期作为目标函数,以实现订单拖期的最小化,本研究将订单无拖期交付作为问题约束,构建了相应的数学规划模型;②在调度时间域上设置加班时间区间,以区别常规工作时间,进而采用加班作业扩大常规生产能力,通过优化调度实现订单无拖期交付;③关于多目标金鹰优化算法的研究主要侧重于连续多目标优化问题的求解,本研究通过有效的编码和解码设计将其用于求解无拖期作业车间调度组合优化问题,并通过仿真调度实验验证了算法的有效性和优越性能。

1 MONTJSSP/O问题描述与建模

1.1 MONTJSSP/O问题描述

所提MONTJSSP/O问题可描述如下:有n个独立的待加工工件和m台可用机器;每个工件都有若干道具有工艺约束的工序,每道工序需要在一台事先确定的机器上加工,且加工时间已知;每个工件都有严格的交货期;在整个计划时间区间内,除了常规的工作时间外,还有一些可拓展使用的时间片段(加班时间);若加班时间被利用,则将产生额外的生产成本;工件交货期不能处于加班时间区间。问题求解目标是优化安排加班时间,确定各工序的加工顺序和开工时间,从而使完成所有工件的工期和总加班时间最小。

此外,MONTJSSP/O问题还遵从以下假设条件:①所有工件和机器零时刻可用;②不单独考虑装设时间和转序时间;③同一时刻下,每台机器只能加工一个工件,每个工件只能被一台机器加工;④工件的加工过程不允许被中断,即不允许工时拆分,不允许被抢占;⑤工件间相互独立,且不存在优先级关系;⑥不考虑机器故障、订单变化和急件插入等动态事件;⑦所有加班时间区间内的单位时间加班成本相同;⑧工件的交货期设置合理,考虑加班作业情况下不至于绝对超负荷。其中,假设①～⑥是研究作业车间调度问题的基本假设[1-4,18];假设⑦主要是为了简化加班成本的计算;假设⑧约定了本研究适用范围,如果交货期设置不合理,则存在不使用加班作业也能实现无拖期交付,或者使用所有加班时间也无法实现无拖期交付的情况。

1.2 数学模型建立

为了方便建立问题数学模型,定义本文中用到的数学符号如表1所示。

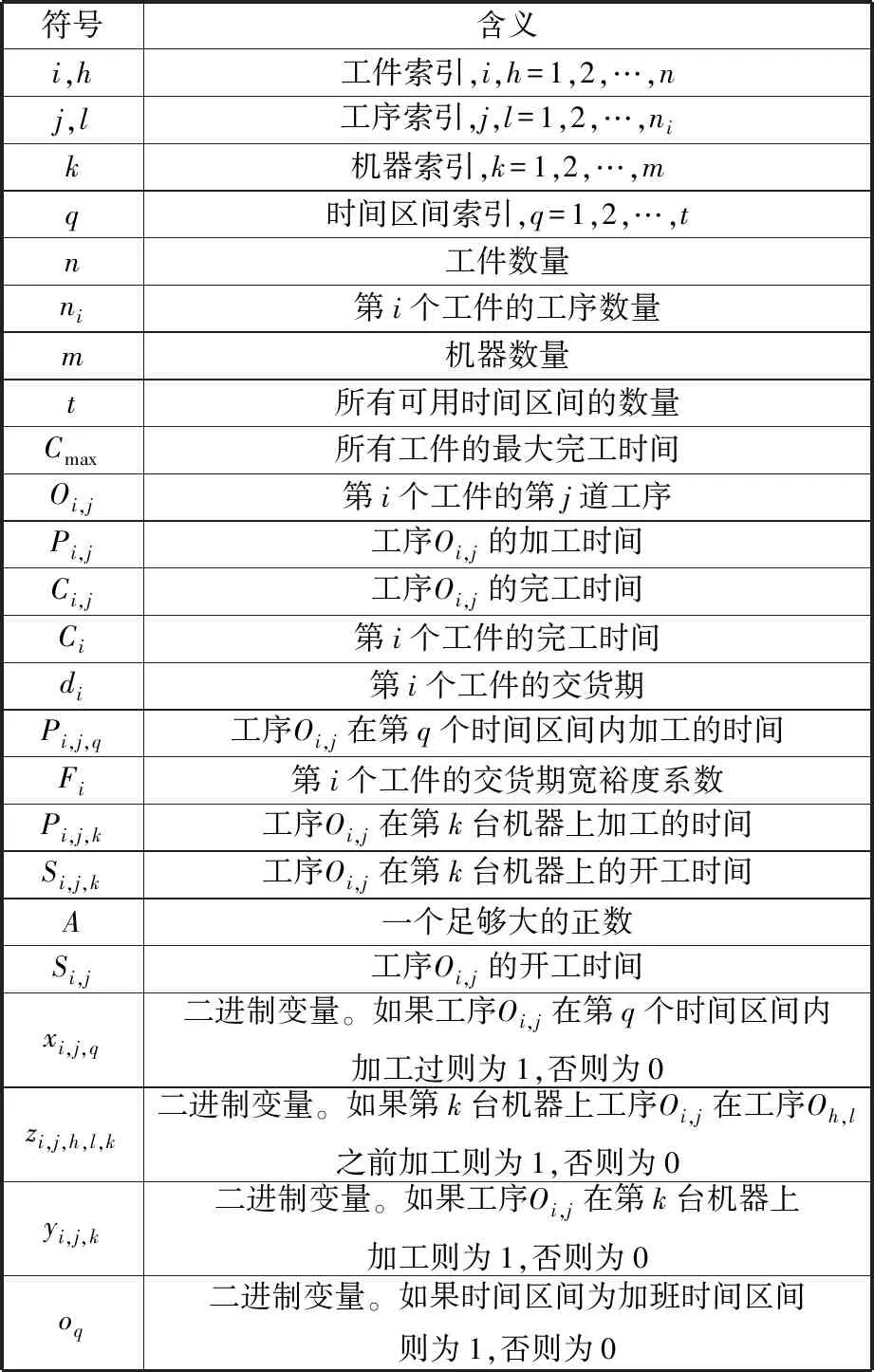
表1 数学符号定义

基于表1所示的符号定义,MONTJSSP/O问题的数学模型可表示如下:

(1)

minf2=Cmax

(2)

满足约束如下:

Ci-di≤0i=1,2,…,n

(3)

Si,j+Pi,j≤Si,j+1

(4)

i=1,2,…,nj=1,2,…,ni-1

Si,j≥0i=1,2,…,nj=1,2,…,ni

(5)

Si,j+Pi,j=Ci,j

(6)

i=1,2,…,nj=1,2,…,ni

(7)

i=1,2,…,nj=1,2,…,ni

(8)

i=1,2,…,nj=1,2,…,ni

(9)

i=1,2,…,nj=1,2,…,ni

Si,j,k+Pi,j,k≤Sh,l,k+A(1-zi,j,h,l,k)

(10)

i,h=1,2,…,nj,l=1,2,…,ni

k=1,2,…,m

其中,式(1)和式(2)表示两个目标函数,分别为最小化总加班时间和最小化最大完工时间;式(3)定义无拖期约束;式(4)和式(5)约束一个工件的工序只能在它的紧前工序加工完成后才能开始加工,且开工时间须在零时刻以后;式(6)表示工序一旦开工就不能被中断;式(7)和式(8)表示工序可在一个或多个时间区间内进行加工,且加工时间等于各时间区间内花费时间的总和;式(9)和式(10)约束一道工序只能在一台机器上加工,且一台机器同时只能加工一道工序。

2 算法设计

与传统作业车间调度问题相比,MONTJSSP/O具有更大的求解难度,主要体现在:①增加了无拖期约束,提高了获得可行解的难度;②增加了加班时间的优化使用决策。本文以期通过对基本多目标金鹰优化算法[13]进行适应性改造来有效求解MONTJSSP/O问题并获得优越性能。

基于精英保留策略的非支配排序金鹰优化算法(NSGEO)对基本多目标金鹰优化算法进行了如下改进:①采用离散编码方式,以实现金鹰优化算法连续空间至MONTJSSP/O离散解空间的映射;②采用两阶段解码方案,以增加满足无拖期约束可行解的数量,并尽可能减少最大完工时间和总加班时间;③嵌入基于精英保留策略的非支配排序选择算子,以加速算法的收敛速度和提高解质量;④引入自适应新个体生成策略,以均衡算法的全局搜索能力和局部寻优能力。NSGEO算法的伪代码如算法1所示。

算法1 NSGEO算法伪代码输入:初始种群Pinit;种群规模Fpop;最大迭代次数Imax;攻击倾向参数[p(0)a,pmaxa];巡航倾向参数[p(0)c,pmaxc]。输出:Pareto最优解集(Pbest)。1 设置当前迭代次数g=0;2 for g in Imax do3 设置当前种群个体序号φ=0;4 采用两阶段解码方案计算所有个体的适应度值;5 对所有个体按适应度值进行非支配排序;6 for φ in Fpop do7 if第φ个个体为精英个体then8 保留该个体不变;9 else10 计算攻击概率pa和巡航概率pc;11 if pc>pa then ∥ exploration phase12 使用交叉和变异组合操作生成新个体;13 else ∥exploitation phase

2.1 编码方式

基本多目标金鹰优化算法通常被用于求解连续优化问题。在算法中,金鹰个体根据文献[13]中式(6)迭代更新自己的位置。由于MONTJSSP/O是离散型优化问题,因此,需要设计有效编码方法将问题解空间映射至算法空间。受遗传算法等进化类优化算法启发,本文采用已广泛使用的基于工件序号的编码方式。图1为2台机器4个工件的编码示意图,案例具体信息如表2所示,其中第1列表示工件序号;第2、3列表示加工信息,圆括号外数字表示工序序号,圆括号内数字表示加工工时;第4列表示各工件交货期。图1所示为该案例的一个编码结果,加工序列中每个基因位上的整数表示工件编号,从左往右,整数编号在加工序列中第j次出现就代表该工件的第j道工序。加工序列的长度为所有工件所有工序数的总和。

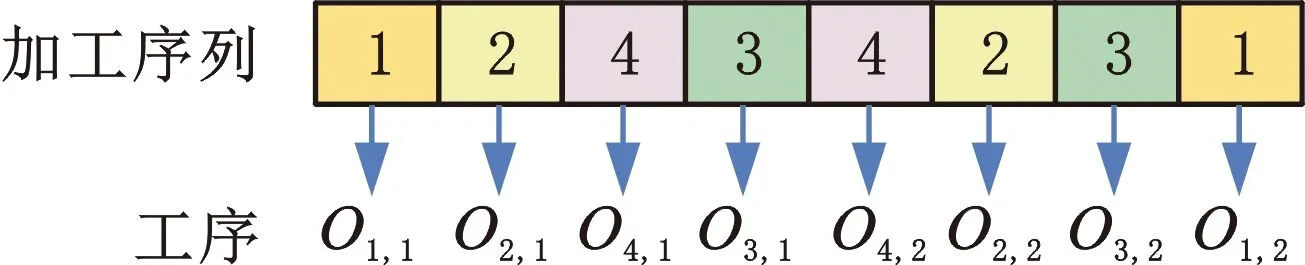
图1 编码方式示例

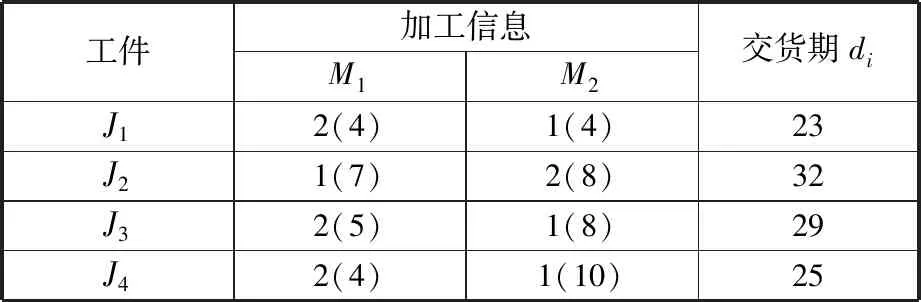
表2 2台机器和4个工件案例信息

2.2 两阶段解码方案

以图1所示的编码为例,采用传统解码方法得到的活动调度解如图2所示,其中d1、d2、d3、d4分别为工件J1、J2、J3、J4的交货期,[8,16]表示加班时间区间,最大完工时间Cmax=31。由图2可以看出,该活动调度解为非法解,工件J1的完工时间(C1=31)超过了其交货期(d1=23),不满足无拖期约束。

图2 传统解码方式调度结果

为此,本文基于问题特征提出了一种两阶段解码方案,具体流程如下:

(1)第一阶段解码。该阶段旨在让所有工序尽早开工,使所有工件最大完工时间尽可能地短。图3所示为第一阶段解码流程。具体方法是:从左往右依次对加工序列上所有基因进行排序,待排工序开工时间需满足同工件工序间的前后约束关系。加工机器上任何加工间隙如果时间足够长,则可在该时间段安排加工该工序。如果该机器上有多个时间区间可用,则选择使用加班时间最少的时间区间。如图3a所示,待排工序O1,2有三种可排位置,但第②种方案既能满足工件J1无拖期交付,也能尽量减少加班时间,所以选择此方案。经过第一阶段解码后的调度结果如图3b所示。若经过第一阶段解码后的排序结果为非法解(即存在拖期),则删除该个体,然后随机生成新个体,并继续执行第一阶段解码过程,如此循环直至得到可行解。若前述循环过程执行30次后仍未得到可行解,则直接结束当前个体的解码过程,继续执行下一个个体的解码过程。

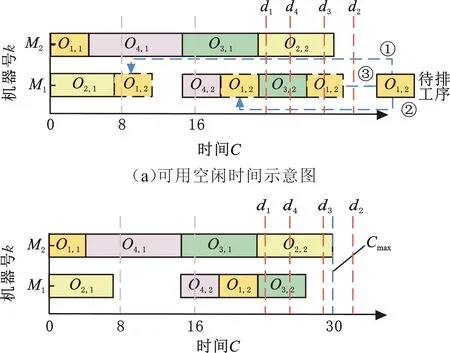
(b)第一阶段解码结果

(2)第二阶段解码。该阶段是在第一阶段解码结果的基础上,保持工件最大完工时间不变,并满足无拖期约束,将所有工序尽量往右移(推迟工序开工时间),将处于加班时间区间的工序尽量移动至常规工作时间区间,从而减少总加班时间。若某道工序右移后加班时间会增加,则保持工序开工时间不变。如图4a所示,在第一阶段解码结果的基础上搜索可以右移的工序。从图4a中可以看出,在满足无拖期约束和Cmax不变的情况下,工序O3,2和O1,2可往右移。当工序O3,2和O1,2移动完成后,工序O4,2也可往后移。由此可知,在此阶段共有三个工序可往右移,工序O4,2右移后减少了总加班时间。第二阶段解码结果如图4b所示。

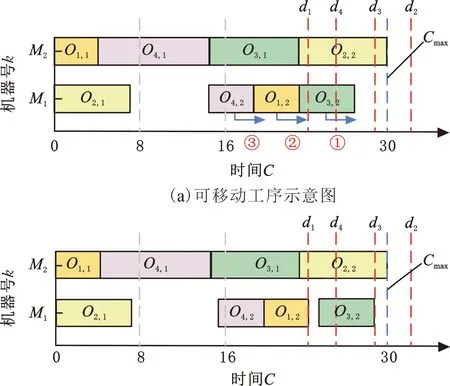
(b)第二阶段解码结果

将两阶段解码方式和传统解码方式得到的解码结果进行对比可知,通过两阶段解码方式得到的解码结果不仅满足了无拖期约束,而且减少了最大完工时间和总加班时间。由图2和图4可以看出,采用传统解码方式得到调度解的最大完工时间为31,总加班时间为10;采用两阶段解码方案得到调度解的最大完工时间为30,总加班时间为9。与传统解码方式对比可知,采用两阶段解码方案使最大完工时间和总加班时间分别减少了1。

2.3 基于精英保留策略的选择算子

受文献[19]的启发,本研究在改进金鹰优化算法中嵌入了基于精英保留策略的选择算子来选择种群中表现更优的个体进入下一代:首先通过非支配等级划分方法按适应度值将种群中所有个体分为若干个非支配等级,然后根据拥挤度距离对同一支配等级下的个体进行排序,最后选择支配等级低、拥挤度大的个体构造新的种群。基于精英保留策略的选择算子具体执行步骤如下。

(1)设当前种群为Pnow,种群规模为Fpop,初始化下代种群Pnext为空集。

(2)计算种群Pnow中个体的非支配等级。首先找出Pnow中非支配最优解,构成第一个非支配最优解层,记为R1,然后将R1中个体从Pnow中去除,再从余下个体{Pnow-R1}中找出新的非支配解,记为R2,依次类推,直到所有个体被分级。

(3)对步骤(2)得到的各等级集合Ri(i≥1)分别计算其中每个个体的拥挤度距离,并按照该距离从大到小对其中的个体进行排序。

(4)遍历当前种群Pnow所有个体,执行如下操作:若当前个体为精英个体(判定依据:种群中所有个体按非支配等级从小到大和各等级中按拥挤度距离从大到小综合排序,排序位于前Fpop×50%的个体被定义为精英个体),则直接将该个体存入集合Pnext;若不是精英个体,则生成新个体并存入集合Pnext。

2.4 自适应子代个体生成策略

在每次迭代过程中,如果个体不是精英个体,则需要重新生成新个体用于下轮迭代。为了兼顾算法的全局搜索和局部寻优能力,本文引入了自适应个体更新策略,具体步骤如下。

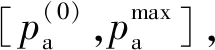
(2)计算当前攻击概率pa和当前巡航概率pc,其计算表达式分别如下:

(11)

(12)

(3)如果pc>pa,则采用POX交叉[20]和两点交换变异组合操作生成新个体;否则,使用基于N5邻域结构的局部搜索[21]方法生成新个体。

基于以上步骤,在迭代初期使用交叉和变异组合操作生成相似度不高的新个体,扩大种群搜索范围,防止算法陷入局部最优;进入迭代后期时,使用局部搜索产生相似度较高的个体,以提高局部搜索能力。

3 仿真实验与结果分析

为了验证NSGEO算法性能,所有算法采用C语言进行编程,并在配置了Intel Core i3 CPU和8G RAM的Windows 10系统中进行了测试。

3.1 算例生成

由于MONTJSSP/O问题不存在标准测试集数据,因此对{FT06、FT10、FT20},{LA01、LA06、LA11、LA16、LA21、LA26、LA31、LA36},{SWV01、SWV06、SWV11、SWV16},{TA01、TA11、TA21、TA31、TA41、TA51、TA61、TA71}共23个作业车间调度问题基准算例进行了改造以满足本问题的研究。为区别于标准算例,改造后的算例名称为在原算例名称前面加上符号m,如mFT06、mLA01、mSWV01和mTA01等。

算例改造体现在时间域的离散化和交货期的设置这两方面。时间域的离散化主要指加班时间和常规工作时间区间的设定,具体规则为:每24小时为一个循环周期,每个循环周期包含16小时的常规工作时间和8小时的加班时间,即[0,16]为常规工作时间区间,[16,24]为加班时间区间。工件交货期采用常用的总工作量(total work content,TWK)规则,具体计算公式为

(13)

式中,i、j分别为工件索引和工序索引,di为第i个工件的交货期;Fi为第i个工件的交货期宽裕度系数;Pi,j为第i个工件第j道工序的加工时间。每个工件的交货期宽裕度系数的取值取决于问题的规模,确定方法将在3.3.1节中介绍。

3.2 性能评价指标

本研究采用三个性能指标来评价算法的优劣性。由于本问题引入了无拖期约束,采用启发式算法求解时极易产生非法解,而可行解的数量直接影响最优解的好坏,因此本文将可行解数量作为一个评价指标。此外,为了综合评价多目标算法的收敛性和解的分布性,本文选择反世代距离(inverted generational distance,IGD)和超体积(hypervolume,HV)两个常用的多目标评价指标。上述两个评价指标的计算方法和评价规则可参考文献[2,5]。

理论上,种群规模和迭代次数的乘积为所有可能解的数量,如种群规模为100,迭代次数为100,则所有可能解的数量为10 000。在问题求解过程中,得到的可行解数量(number of feasible solutions,NFS)越多,则搜索到最优解的可能性越大,表明算法性能越好。

3.3 实验结果及性能分析对比

为了验证NSGEO算法求解MONTJSSP/O问题的性能,本节首先验证了改进项对算法性能的影响,然后将NSGEO算法与其他三种多目标优化算法进行了对比实验分析。

3.3.1两阶段解码的性能分析

为了验证两阶段解码方案的有效性,使用基本遗传算法进行了实验,将求解过程中产生的可行解数量(NFS)作为评价指标。实验中,设置种群规模为100,迭代次数为100。由于交货期的设置会直接影响订单是否能按期交付,因此在不同交货期宽裕度系数F(F=2,4,6,8)下进行了实验,实验结果如表3所示,其中SD列和TD列分别表示通过传统解码(standard decoding,SD)方式和两阶段解码(two-stage decoding,TD)方式实验后得到的可行解数量。

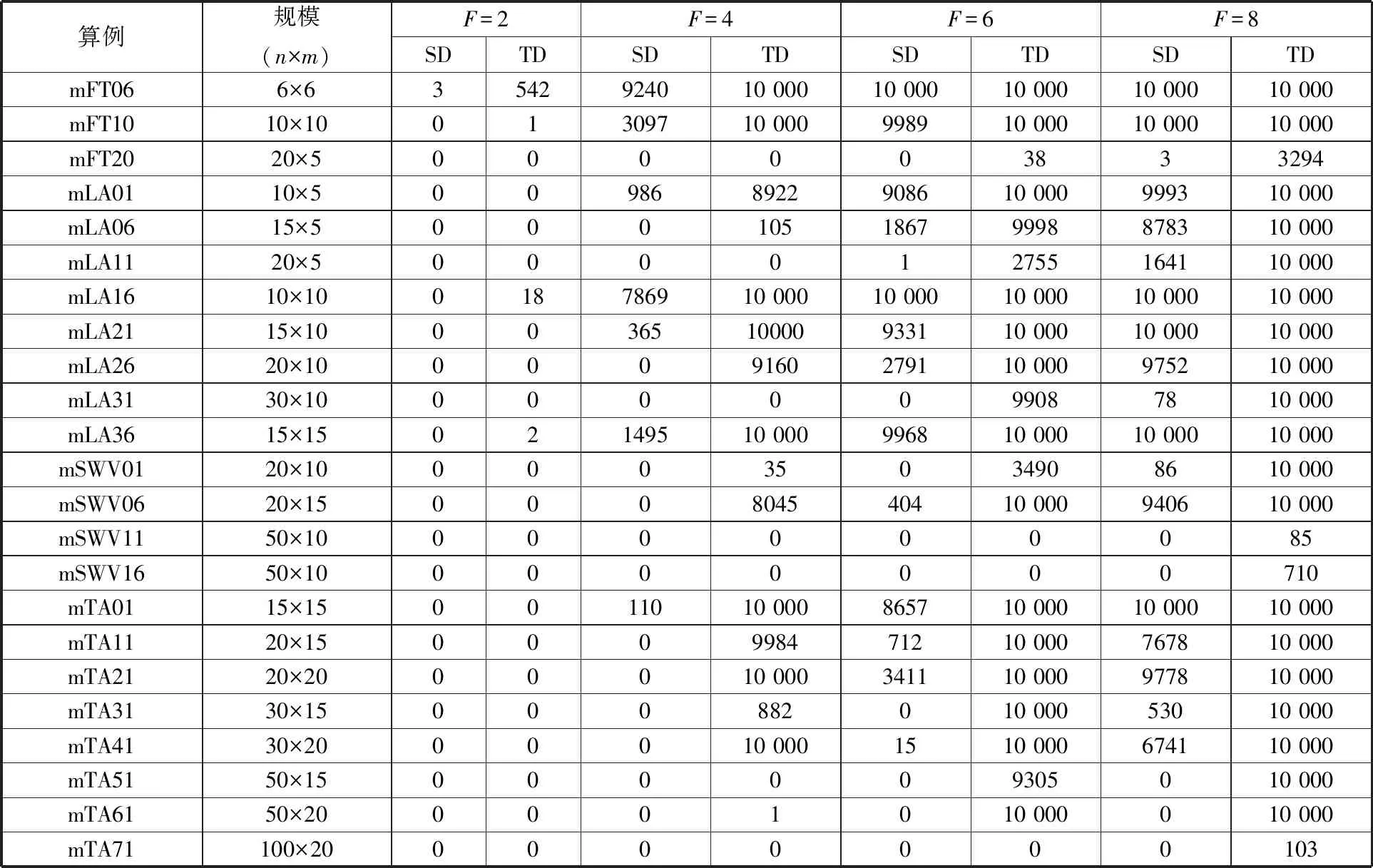
表3 传统解码和两阶段解码方案下得到的可行解数量对比

从表3中可以发现,在合理F值下,两阶段解码方案比传统解码方式更加有效。比如:F=2时,所有23个测试算例中,通过SD方式只有mFT06算例能得到3个可行解,但TD方式有mFT06、mFT10、mLA16和mLA36共4个算例能得到可行解,且mFT06算例能得到542个可行解;F=4时,通过SD方式只有30%的算例能得到可行解,但通过TD方式有70%的算例能得到可行解,且TD方式得到的可行解数量远大于SD方式得到的可行解数量;F=8时,所有算例可通过TD方式得到可行解,但通过SD方式还有5个算例未能得到可行解。

通过以上分析可以看出,两阶段解码方案在得到可行解数量方面是有效的,与传统解码方式相比具有很大的优势。此外,从表3中还可以看出交货期宽裕度系数对可行解数量的影响很大。若F值过小,可行解数量太少或为零,说明交货期太紧,无法通过优化实现无拖期;若F值太大,则交货期太松,与实际生产情况不符。为此,本文以两阶段解码方案下产生的可行解数目大于50为依据,确定了各测试算例下的交货期宽裕度系数。显然,按此方法确定的工件交货期可满足本文1.1节中的问题假设⑧。

3.3.2不同配置多目标金鹰优化算法的性能比较

为检验NSGEO算法中各项改进对问题求解性能的影响,采用三种不同配置的多目标金鹰优化算法(MOGEO)进行了仿真调度实验(两阶段解码方案的有效性在3.3.1节已得到验证,本节实验在三种比较算法中均加入两阶段解码方案)。三种多目标金鹰优化算法的配置情况见表4。

表4 三种多目标金鹰优化算法配置项

为确定较好的算法控制参数,通过田口实验进行了先导性试验,所得较优的算法控制参数为:种群规模取100,最大迭代次数取2000,攻击倾向参数pa取[0.5,2],巡游倾向参数pc取[1,0.5]。

针对所有算例,各算法独立运行10次,采用IGD、HV两个评价指标比较算法的性能,对比结果如表5和图5所示,其中F列表示各改造算例中交货期宽裕度系数的取值。

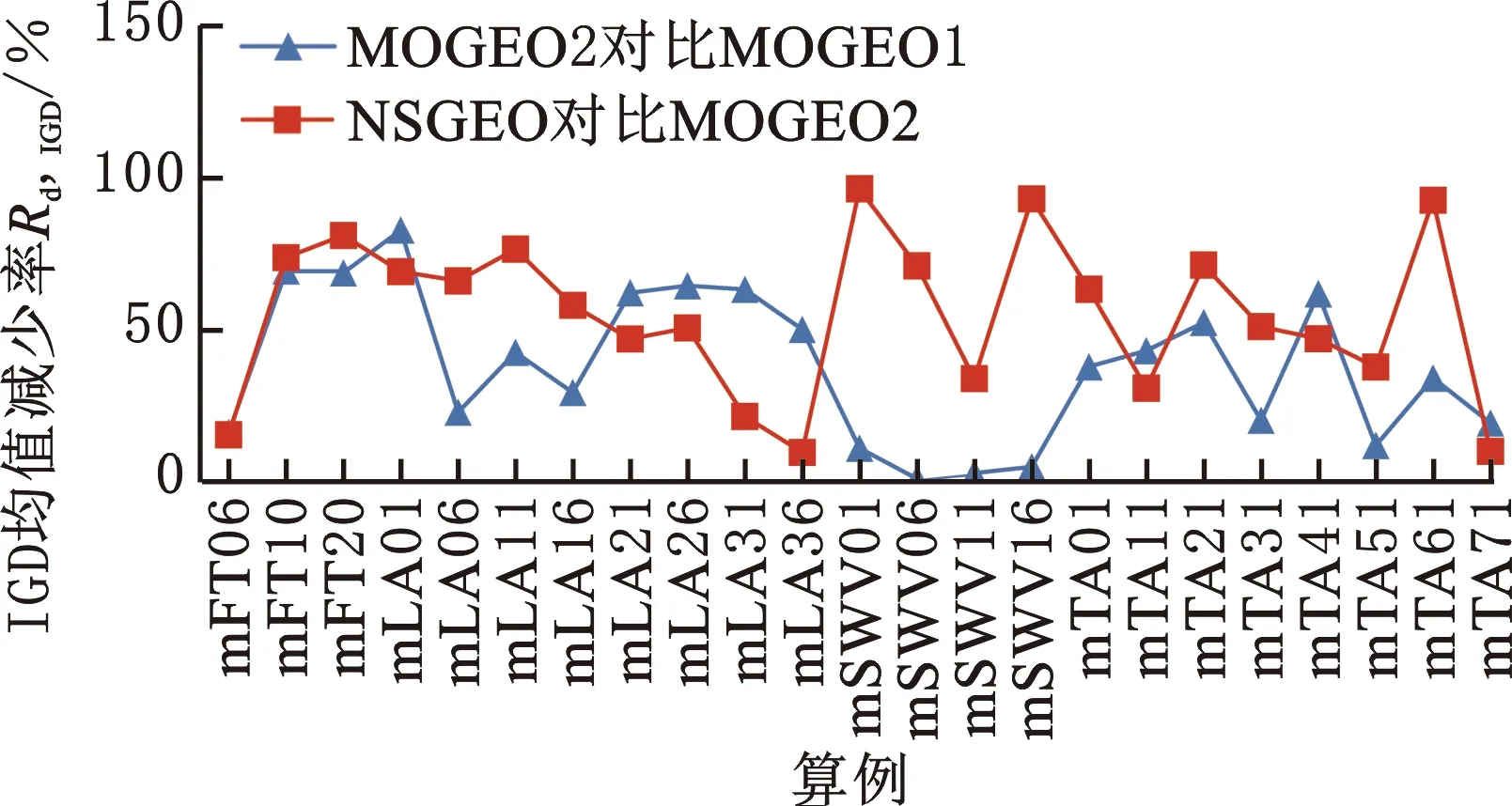
(a)IGD均值减小率曲线

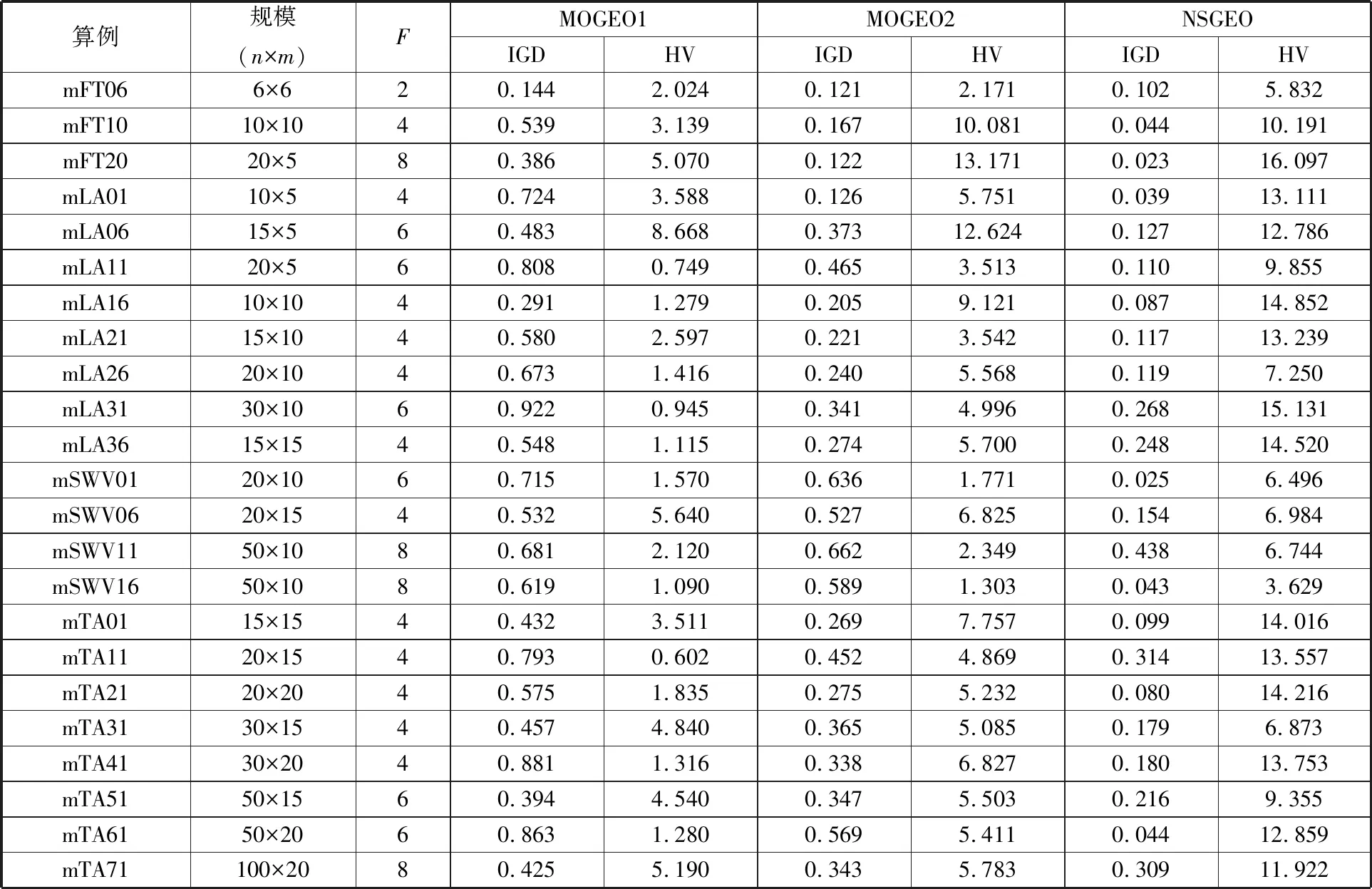
表5 算法改进项有效性分析

通过表5数据和图5曲线可见:

(1)MOGEO2算法与MOGEO1算法相比,前者得到的IGD均值更小,减小率最大达到了82.5%,如图5a所示;前者得到的HV均值也更大,56%的算例中HV均值增长率超过100%,如图5b所示。统计数据表明自适应子代个体生成策略有效地提升了算法性能。

(2)NSGEO算法与MOGEO2算法相比,在23个测试算例中,前者相比于后者有11个算例的IGD均值减小率超过60%,如图5a所示;14个算例中的HV均值增长率超过100%,如图5b所示。由此可知,带精英保留策略的非支配排序选择算子对算法性能提升很大。

综合以上分析,各改进项对多目标金鹰优化算法求解MONTJSSP/O问题的性能提升有效,且效果明显。

3.3.3NSGEO算法与其他多目标优化算法的性能比较

为进一步验证NSGEO算法求解MONTJSSP/O问题的优越性,本文将NSGEO算法和当前求解多目标优化问题常用的基于分解的多目标进化算法(multi-objective evolutionary algorithm based on decomposition,MOEA/D)[22-23]、带精英保留策略的非支配排序遗传算法(non-dominated sorting genetic algorithm-Ⅱ,NSGA-Ⅱ)[21, 24]和混合遗传禁忌搜索算法(hybrid genetic algorithm-tabu search,HGATS)[18,25]三种算法的性能进行了对比。算法具体参数设置如表6所示。为了保证公平性,四种算法的共有参数设置相同值,种群规模均为100,最大迭代次数均取2000。

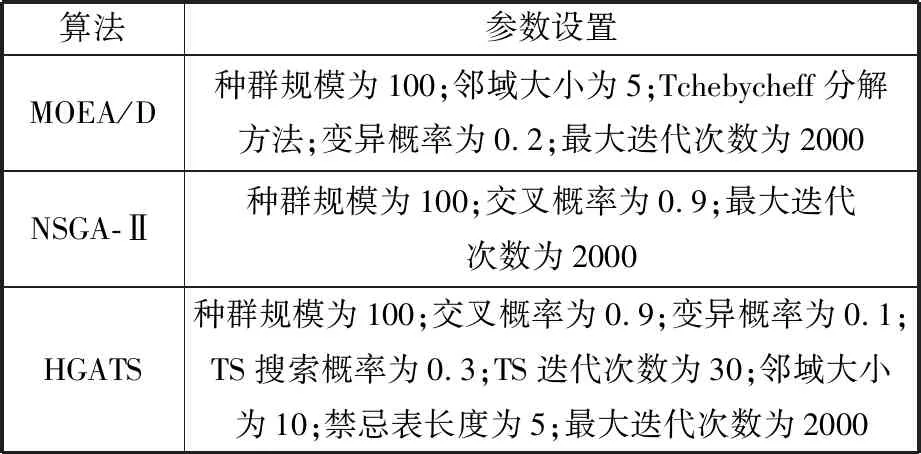
表6 对比算法参数设置

本节采用3.2节描述的IGD和HV两个性能评价指标来对比分析四种算法的性能。表7和表8分别给出了四种算法在每个算例上独立运行10次后两个性能指标的均值和标准差,粗体字部分表示均值最佳值。

表7 NSGEO、MOEA/D、NSGA-Ⅱ和HGATS四种算法IGD对比

表8 NSGEO、MOEA/D、NSGA-Ⅱ和HGATS四种算法HV对比

表7所示为四种算法得到的IGD指标结果,从表中可以看出,与其他三种算法相比,NSGEO算法在23个测试算例中的IGD均值最小,说明NSGEO算法在所有算例中求解得到的Pareto前沿面与真实Pareto前沿面更加接近,即NSGEO算法所得到解的质量更高。

为更加清楚地展示各测试算例通过不同算法所得到的IGD均值及标准差的分布,图6给出了四种对比算法得到的IGD均值和标准差分布曲线。从图6a中可以明显看出:MOEA/D算法和HGATS算法得到的IGD值比NSGA-Ⅱ算法和NSGEO算法得到的IGD值相对更大;虽然NSGA-Ⅱ算法在56%的算例上得到的IGD值与NSGEO算法对应得到的IGD值相近,但在其他算例上与NSGEO算法相差较大,如mLA01、mSWV11和mTA11。总体来说,对于所有测试算例,NSGEO算法比其他三种算法得到的IGD值更小。此外,从图6b中可以发现NSGEO算法在大多数测试算例上标准差更小。对于算例mFT20、mLA21、mTA01和mTA41,与MOEA/D算法和NSGA-Ⅱ算法相比,NSGEO算法得到的IGD标准差更大,但该算法得到的IGD均值更小。综合上述分析,NSGEO算法在IGD评价指标上明显优于其他三种对比算法,具备更好的收敛性、多样性和稳定性。

表8和图7分别展示了四种算法得到的HV指标结果数据以及HV均值和标准差分布曲线。从图7a中可以看出,NSGEO算法得到的HV均值比其他三种算法得到的HV均值大很多,有近74%的算例增长率超过50%,可见NSGEO算法相较于其他三种算法有明显的优势。对于HV标准差,由图7b可见,少数算例NSGEO算法得到的HV标准差比其他算法得到的HV标准差稍大,但差值并不明显,总体来看,NSGEO算法得到的HV标准差更小,算例间的波动也较小。从上述分析不难看出,NSGEO算法的HV指标值优势比较明显,表明NSGEO算法比其他三种算法得到的解质量更高,性能更加稳定。

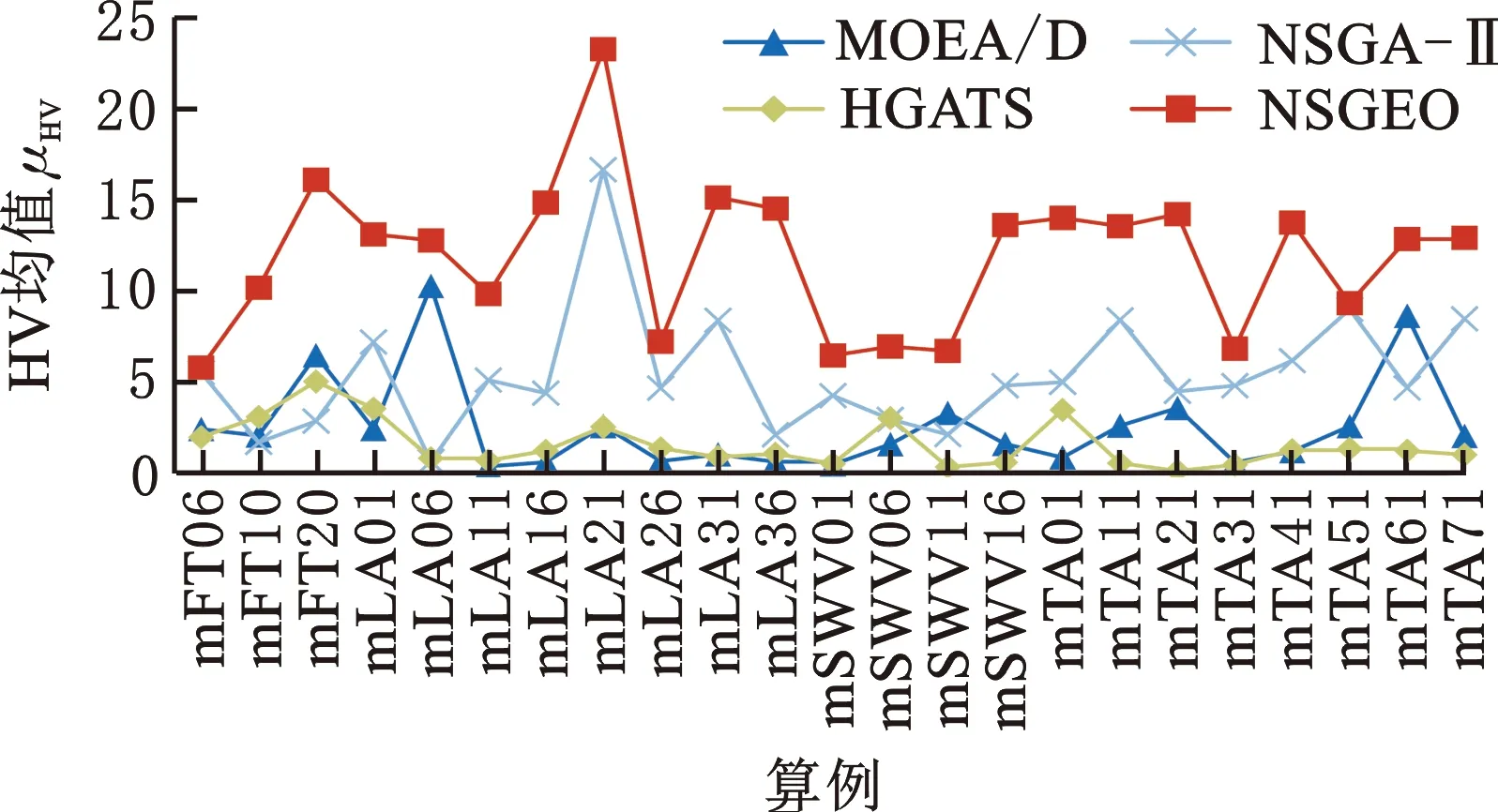
(a)HV均值曲线

为比较直观地观察到各算法得到的Pareto解集的分布情况,对所选择的6个不同规模算例某次运行的结果进行了展示,如图8所示,其中不同形状的点代表不同算法获得的解集。从图8中可以看出,本文研究的两个目标之间存在冲突关系。从Pareto解集的分布可以定性发现,NSGEO算法得到的Pareto解基本都支配着其他三种算法得到的Pareto解,而其他三种算法得到的Pareto解集之间存在相互支配关系。这种分布说明NSGEO算法得到的Pareto解集更接近真实Pareto前沿,解的质量更优。从解的多样性来说,对于算例mTA51,虽然NSGEO算法得到的Pareto解集相对于NSGA-Ⅱ算法稍差,但NSGEO算法得到的Pareto解集更接近真实的Pareto前沿,收敛性更好。从实用性角度来看,对于6个展示的算例,NSGEO算法得到的解的个数相对更多,说明供决策者可选择的方案越多。

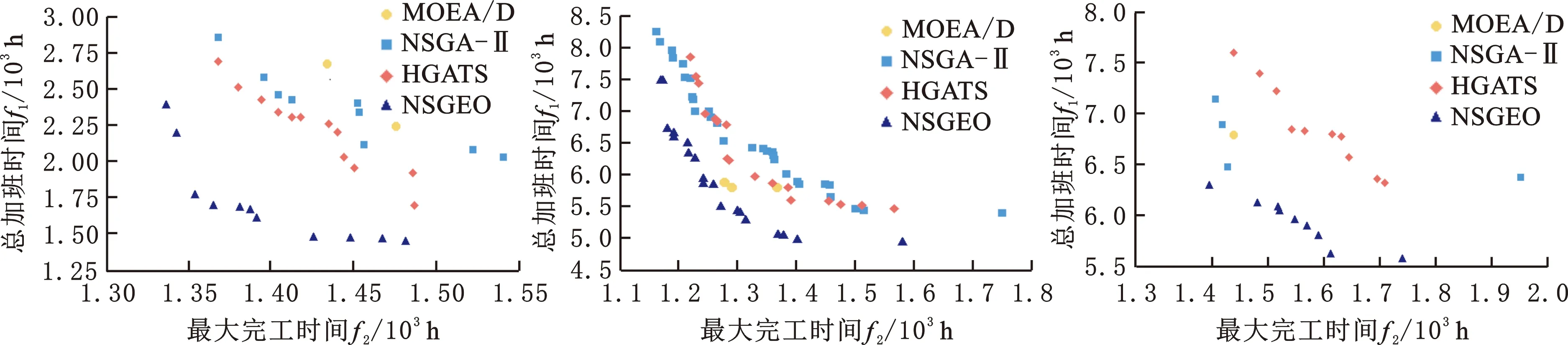
(a)mFT20 (b)mLA21 (c)mLA36

综上所述,NSGEO算法能够求解本文所提出的问题,并且在求解过程中具备比MOEA/D、NSGA-Ⅱ和HGATS三种算法更好的全局搜索和局部寻优能力。

4 结论

为了有效解决面向订单型制造企业合理使用加班时间实现无拖期交付的问题,本文以最小化加班时间和最大完工时间为目标建立了问题的数学模型,提出了一种基于精英保留策略的非支配排序金鹰优化算法(NSGEO)对问题进行了求解,得出了以下结论:

(1)通过分析考虑加班作业的多目标无拖期作业车间调度问题(MONTJSSP/O)和基本多目标金鹰优化算法特点,设计了一种离散编码方式,将金鹰优化算法连续空间映射至问题离散解空间,使问题易于通过启发式算法进行求解。

(2)与传统解码方式进行了对比实验,结果表明,在合理交货期设置情况下,本文提出的两阶段解码方案得到的可行解数量远大于传统解码方式得到的可行解数量,表明采用所提出的解码方式求解MONTJSSP/O问题是有效的,且效果显著。

(3)通过比较不同配置下的多目标金鹰优化算法性能可得,基于精英保留策略的非支配排序选择算子和自适应子代个体生成策略对多目标金鹰优化算法的性能均有显著提升。

(4)通过比较不同测试算例上的仿真调度实验和算法,验证了采用所提NSGEO算法在求解MONTJSSP/O问题时,既保证了算法的收敛性又很好地兼顾了Pareto解集的分布性,而且对解决不同规模问题的稳定性上也明显优于其他对比算法。

通过加班作业扩充生产能力是保证订单无拖期交货的有效措施。然而,若订单过于密集和交货期设置太紧,进而使得制造系统负荷超过一定极限时,则需结合其他资源扩展方式以实现订单的无拖期交付,如机器柔性、工艺柔性和外协加工等。为此,后续可对融合多种可扩展资源的作业车间无拖期调度问题进行进一步的研究。此外,实际制造系统中的调度问题大多属于动态调度问题,为此,在本文研究基础上,需对动态作业车间无拖期调度问题进行进一步的相关研究。