成本结构离散的两属性电子逆向拍卖机制设计

黄　敏,钱小虎*,金东洋,王兴伟

(东北大学信息科学与工程学院;流程工业综合自动化国家重点实验室(东北大学),辽宁沈阳110819)

成本结构离散的两属性电子逆向拍卖机制设计

黄敏,钱小虎*,金东洋,王兴伟

(东北大学信息科学与工程学院;流程工业综合自动化国家重点实验室(东北大学),辽宁沈阳110819)

在由一个采购商和多个供应商组成的电子逆向拍卖系统中,针对供应商成本结构离散且成本和交货期是其私有信息的两属性机制设计问题,为采购商提出一个新的基于协商的多轮逆向拍卖机制.建立基于协商的两层分布式决策模型,提出基于交货期偏差量的交货期让步策略、基于总体目标值的交货期让步策略和基于总体目标值的带有随机的交货期让步策略,并通过数值算例验证了所提让步策略的可行性和有效性.最后通过随机算例对所提的三种让步策略进行对比分析,结果表明基于总体目标值的带有随机的交货期让步策略具有最佳的协商效果.

电子逆向拍卖;机制设计;两层分布式决策模型;协商;交货期让步策略

1　引　言

电子逆向拍卖(electronic reverse auctions,ERA),是一个采购组织和一组预先审核合格的供应商之间的在线实时动态拍卖系统.采购组织明确规定产品或服务的设计、质量、数量、交货期等相关条款,供应商必须在规定的时间内通过连续降价投标来赢得向采购组织提供产品或服务的合同[1],通常采购组织根据投标结果选择具有竞争力的供应商.

随着信息技术的飞速发展和全球化市场竞争的日益激烈,传统的采购模式已难以快速响应市场需求、赢得市场竞争.作为一种新的采购模式,ERA成为政府采购和大型企业采购降低成本、提高效率和优化资源的重要战略选择[1-3],其运行和发展也是学术界关注的热点.目前,ERA已经成功应用于通用电气(General Electric)、通用汽车(General Motors)、柏克德(Bechtel)等制造和服务公司[1,4],受到企业界的广泛关注.因此,对ERA展开研究可以说既有很高的学术价值,更有重要的应用意义.

目前,关于ERA机制设计的研究依据采购商和供应商的决策地位不同主要包括两个方面:

一方面研究供应商静态投标拍卖机制.文献[5]以政府采购为背景,首先研究了考虑价格和质量的两属性逆向拍卖问题,设计了打分函数拍卖机制(scoring rule auction),并证明了二维的收益等价定理.文献[6]以零售业为背景,考虑价格和采购量两个属性,设计了带有入场费的最优供应合同拍卖机制(supply contract auction),并证明该机制与供应商数目无关,但没有考虑完成交易的其他成本(如运输成本、税费、货物检验成本等).文献[7]假设其他成本是采购商的私有信息,设计了考虑供应商的报价和其他成本的两属性逆向拍卖机制,并分析了其他成本对采购商收益的影响,但没有对供应商投标中的非价格属性进行审查.文献[8]设计了考虑供应商审查的逆向拍卖机制,并说明当审查费用较低时,预先审查对采购商来说是有益的,但是当审查费用较高时,事后审查是采购商明智的选择.针对供应源有限的情形,文献[9]设计了考虑合作激励的多属性逆向拍卖机制,并通过仿真分析说明对采购商而言,该机制比现有的不带激励的拍卖机制具有更高的效用.针对重复采购问题,文献[10]设计了基于供应商历史绩效的马尔科夫决策机制,数值分析结果表明对采购商而言,该机制比基于绩效得分(performance score-based)的选择机制具有更高的效用和更好的质量.上述文献均假设采购商为主导的决策情形,针对不同的问题为采购商设计不同的逆向拍卖机制,但现实中采购商与供应商常常处于对等决策地位,且双方具有更多的不对称信息.

另一方面则研究供应商动态投标拍卖机制.文献[11]首先考虑带有数量折扣的组合逆向拍卖机制设计问题,假设供应商的成本结构是离散的,建立带有数量折扣的组合逆向拍卖胜者确定问题的模型,提出多轮动态逆向拍卖机制,但仅考虑了单一属性价格.针对多属性动态逆向拍卖机制设计问题,文献[12]假设采购商知道供应商的成本结构和投标策略,根据据供应商每一轮的投标结果,采用逆向优化(inverse optimization)方法设计最优逆向拍卖机制,从而使采购组织的利润最大,但假设供应商的成本结构是连续的.对于供应商成本结构离散的多属性逆向拍卖问题,文献[13]假设供应商采用近视最优反应(myopic best-response,MBR)投标策略,设计了考虑供应商之间的信息泄露的动态逆向拍卖机制,并证明该机制是改进的VCG机制,但没有基于采购商的视角进行研究.文献[14]针对供应商供应能力有限的逆向拍卖机制设计问题,基于采购商的视角设计了嵌入线性规划动态求解的最优拍卖机制,分析了博弈论框架下供应商的顺序投标策略,并给出胜标者的上确界.对于考虑制造商生产计划的逆向拍卖问题,文献[15]基于采购商的视角建立了双层分布式决策模型,分别描述采购商和制造商的决策过程,并通过优化方法求解双层模型中的分配量、交货期、报价和生产计划.针对竞价人数不足的网上逆向组合拍卖问题,文献[16]提出一种捆绑与组合相结合的两轮拍卖机制,数值分析结果表明该机制可以提高拍卖人的经济收益.上述文献均假设采购商知道供应商的决策偏好,针对不同的问题研究采购商的逆向拍卖机制,但现实中存在供应商决策偏好是未知的情况.

综上,现有文献没有同时考虑供应商成本结构离散且决策偏好未知的逆向拍卖机制设计.而现实采购中,由于数量折扣供货模式可以提高供应商的收益[17],供应商在供货时通常采用数量折扣模式,如全球最大的食品生产商之一玛氏公司(Mars)在采购时要求供应商提供数量折扣的供货模式[11],此时供应商的成本结构是离散的.同时,采购商通常不知道供应商的决策偏好.并且信息不对称情况下的动态逆向拍卖机制能使采购商的采购费用更低[18].因此对供应商成本结构离散且供应商决策偏好未知的动态逆向拍卖机制设计问题展开研究,具有理论和实际意义.

本文基于采购商的视角,就这一类现实中的问题展开研究,提出基于协商的多轮逆向拍卖机制.与文献[15]相比,本文有四个重要的不同之处:其一,本文考虑的是采购商和供应商(分销商或零售商)之间的问题,采购商决策分配量和交货期,供应商决策报价;而文献[15]考虑的是采购商和制造商之间的问题,采购商决策分配量和交货期,制造商决策报价和生产计划.其二,本文假设供应商的决策偏好是未知的,即供应商的决策模型未知,采购商只知道供应商以一定的概率选择某种策略,但不知道供应商具体选择哪种策略;而文献[15]假设供应商的决策偏好是已知的,即供应商的决策模型已知,采购商知道供应商只需优化相应的决策模型,供应商的决策是确定的.其三,对所建立的双层分布式决策模型,本文通过基于协商的让步策略和基于优化的方法对上层模型进行求解,即通过优化方法确定分配量,通过采购商让步策略确定交货期,同时通过供应商让步策略确定下层模型的最优报价;而文献[15]主要是通过优化的方式来求解双层模型的,即通过KKT优化条件(Karush-Kuhn-Tucker optimality conditions)和最大最小决策方法(max-min decision concept)将双层模型转化为单层模型进行求解,对转化后的上层模型进行优化可确定分配量和交货期,对转化后的下层模型进行优化可以确定生产计划和最优报价.其四,本文的协商终止准则是达到最大协商次数或连续5次协商结果不变,由采购商和供应商共同决定;而文献[15]实质上是一个双层优化问题,并没有协商过程.

本文首先建立了基于协商的两层分布式决策模型,用于刻画采购商和供应商的决策与信息交互过程.进而提出基于交货期偏差量的交货期让步策略、基于总目标值的交货期让步策略和基于总目标值的带有随机的交货期让步策略,并通过数值算例验证了所提让步策略的可行性和有效性.最后通过50组随机算例对这三种让步策略进行对比,结果表明基于总目标值的带有随机的交货期让步策略好于其他两种让步策略.

2　问题描述及模型

2.1问题描述

在考虑价格和交货期两属性的ERA中,采用基于协商的多轮密封投标方式进行采购:采购商首先公布采购量和供应商的初始分配量及初始交货期;然后供应商间接竞标,即根据自己的成本结构以及分配量和交货期进行密封投标,其投标结果将影响采购商的分配决策;最后采购商调整每个供应商的分配量和交货期,同时判断是否满足协商终止准则,如果不满足,则进入下一轮协商.

模型基本假设如下:

假设1采购商向供应商购买Q个同类商品,供应市场货源充足,但供应商i(i=1,2,...,n,n＞2)的供应能力有限,其最大供应量为

假设2供应商的成本结构具有批量折扣和交货期折扣的特征,为简单起见,设单位成本随着批量和交货期的增加而降低.

假设3采购商的费用和交货期的预算分别为c0和d0,即实际费用和交货期与预算的偏差越小越好.

假设4供应商的报价策略带有随机性,获得分配量的供应商以较小的概率降价,未获得分配量的供应商以较大的概率降价.

假设5采供双方都是风险中性的理性决策者,其中采购商的目标是最小化实际费用与期望费用的偏差率和实际交货期与期望交货期的偏差率,供应商的目标是在最低报价的约束下获得更多的分配量.

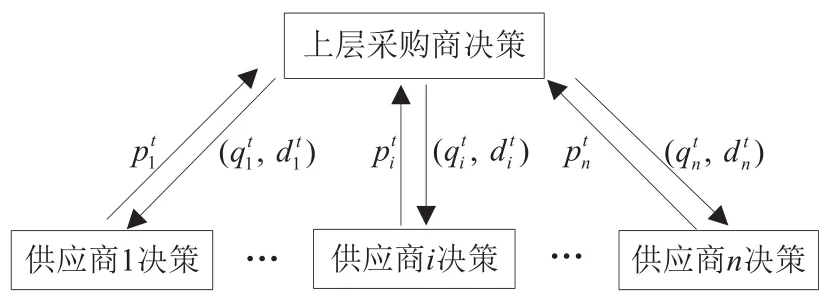
图1　采购商与供应商的信息交换过程Fig.1　The information exchange process between buyer and suppliers

2.2两层分布式决策模型

针对上述问题,采购商首先根据上一轮的交货期和报价决策本轮的最优分配量,然后根据上一轮的分配量和本轮的分配量来决策本轮的交货期;而供应商根据上一轮的分配量、本轮的分配量和交货期决策报价.为此,构建确定最优分配量和最优报价的两层分布式决策模型如下.

上层决策,即采购商决策模型(TM)为

下层决策,即供应商决策模型(BM)为

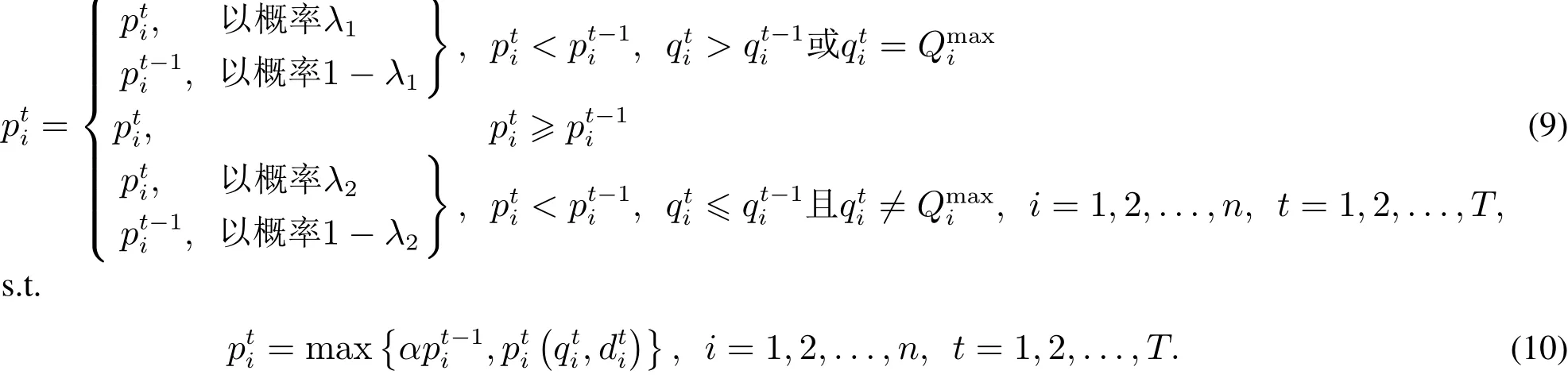
上述各式中符号、参数及变量含义如下:

t为拍卖轮数,t=1,2,...,T;

Ti为采购商与供应商i进行交易的费用,即交易费用;

wc为费用偏差率权重,0＜wc＜1;

wd为交货期偏差率权重,0＜wd＜1,且wc+wd=1;

α为供应商报价的降价幅度,0＜α≤1;

λ1为供应商本轮的分配量大于上一轮的分配量时降价的概率;

λ2为供应商本轮的分配量小于上一轮的分配量时降价的概率.

上层采购商根据上一轮报价决策本轮分配量,目标函数如式(1)所示,包括两部分:采购费用的偏差率和交货期的偏差率;式(2)表示采购需求;式(3)是供应商的能力约束;式(4)是实际采购费用与目标费用的偏差量约束;式(5)表示实际交货期与期望交货期的偏差量约束;式(6)表示是否选择供应商;式(7)是分配量和交货期偏差量约束,本文假设分配量和交货期均为整数;式(8)是采购费用偏差量约束.

下层供应商根据上层采购商传递的分配量和交货期进行报价,其报价让步策略如式(9)所示:当本轮的报价大于上一轮报价时,按本轮报价;当本轮报价小于上一轮报价且本轮的分配量大于上一轮的分配量或等于最大供应量时,以较小的概率按本轮报价(即降价),以较大的概率按上一轮报价(即不降价);当本轮报价小于上一轮报价且本轮的分配量小于上一轮的分配量时,以较大的概率按本轮报价(即降价),以较小的概率按上一轮报价(即不降价).式(10)是供应商的降价策略,为了获得更多的分配量,供应商会以降价系数α按照上一轮的报价进行降价,但如果降价后的报价低于成本价,则按成本价报价.

3　基于协商的多轮逆向拍卖机制设计

基于协商的多轮逆向拍卖机制设计主要包括拍卖启动阶段初始量设置、采购商决策过程设计、供应商决策过程设计及协商终止准则设计.拍卖启动时,上层采购商首先向下层供应商传递初始分配量和初始交货期,供应商根据采购商传递的分配量和交货期确定初始报价,并计算此时的交易目标值.此后,采购商首先根据供应商的报价求解上层模型(TM),确定最优分配量,并根据交货期让步策略确定交货期;然后供应商根据采购商传递的分配量和交货期求解下层模型(BM),并进行报价,直到协商终止.

基于协商的多轮拍卖机制流程具体如下:

步骤1拍卖启动阶段初始量设置

步骤1.1拍卖启动,t=1;

步骤1.2上层采购商分配给下层每位供应商相同的分配量q和相同的交货期d(若超出供应商的最大供应能力,则自动按最大供应能力分配);

步骤1.3下层每位供应商根据上层采购商传递的分配量和交货期,确定自己的最低报价并按最低报价的w倍进行报价;

步骤1.4采购商确定初始投标目标值G0和初始交易目标值

步骤2上层采购商决策过程

步骤2.1上层采购商在获得下层每位供应商递交的报价后,通过求解上层模型(TM)对采购量进行重新分配;

步骤2.2上层采购商根据下层供应商本轮和上一轮的分配量设计相应的交货期让步策略,同时根据交货期让步策略确定新的交货期;

步骤3下层供应商决策过程

步骤3.1下层供应商根据获得的分配量和上层采购商对交货期的决策,确定自己的最低报价

步骤3.2下层供应商通过求解下层模型(BM)确定本轮的投标价格;

步骤4协商终止准则

步骤4.1本轮竞标结束后,上层采购商计算本轮的投标目标值Gt;

步骤4.2上层采购商将本轮的投标目标值与上一轮的交易目标值进行比较,若对本轮投标结果满

步骤4.3判断是否满足协商终止条件,如果满足,则协商终止,进行交易;否则,进行下一轮协商, 即t=t+1,并跳转到步骤2.

3.1拍卖启动设置

拍卖开始时,由上层采购商首先向下层每家供应商传递两个启动量:采购数量和交货期.为使得分配具有公平性,对每家供应传递的两个启动量分别保持相同,设为下层每家供应商则根据这两个量向上层采购商递交自己的报价.首先,每家供应商根据上层采购商分配的采购量和指定的交货期,找出对应的最低报价,然后以最低报价的w(w＞1)倍进行投标,即

3.2采购商采购量决策方法

采购商通过下层供应商上一轮的报价决策本轮的采购量分配方案,通过分配采购量影响供应商的报价决策,使想要获得更多分配量的供应商降低报价.由于考虑供应商供应能力的上层模型(TM)是NP难问题,对于小规模的问题通常采用枚举算法进行求解,对于大规模的问题则可以通过启发式算法或遗传算法等智能优化算法进行求解.

3.3采购商交货期让步策略

由于交货期对拍卖结果具有较大的影响,因此本文提出三种交货期的让步策略:基于交货期偏差量的交货期让步策略、基于总目标值的交货期让步策略和基于总目标值的带有随机的交货期让步策略,分别记为策略1、策略2和策略3.下面重点介绍这三种让步策略.

3.3.1基于交货期偏差的交货期让步策略

由于上层模型(TM)通过分配量的多少间接控制供应商的报价,使实际费用与期望费用的偏差最小,而采购商的目标是实际费用和交货期与期望费用和交货期的偏差率最小化,因此采购商需要制定相应的交货期让步策略,使实际交货期与期望交货期的偏差最小.本文首先考虑基于交货期偏差量的交货期让步策略,记为策略1.策略1的基本思想是,当实际交货期大于期望交货期时,采购商通过降低交货期可以减小交货期偏差;同时,当实际交货期小于或等于期望交货期时,采购商通过增加交货期可以降低费用偏差.定义

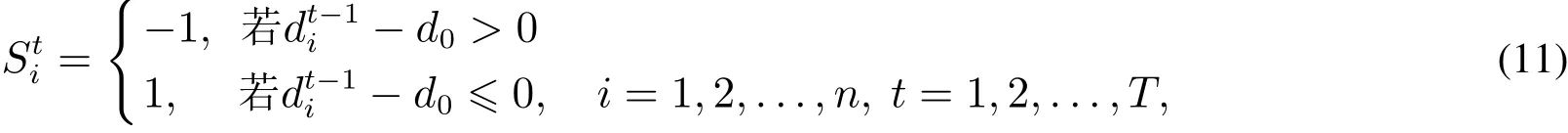
为第t轮供应商i交货期的变化趋势.

设Di为供应商i的交货期集合,则采购商对供应商交货期dti的决策为

式(11)表示若上一轮的交货期大于期望交货期,则减小本轮的交货期;否则增加本轮的交货期;式(12)表明如果本轮所求得的交货期属于交货期集合Di且不小于期望交货期,则按本轮算得的交货期成交;否则按上一轮的交货期成交.

3.3.2基于总目标值的交货期让步策略

策略1是从局部进行考虑的,仅通过交货期偏差决策交货期,带有一定的局限性,因此提出改进的基于总目标值的交货期让步策略,记为策略2.策略2的基本思想是,当目标值减小时则按照上一轮交货期的变化方向确定交货期,否则按照上一轮交货期变化的反方向确定交货期.具体描述如下.

第一轮,与策略1相同,根据实际交货期与期望交货期的偏差量确定交货期,如式(11)–式(12)所示.此后(t≥2),定义

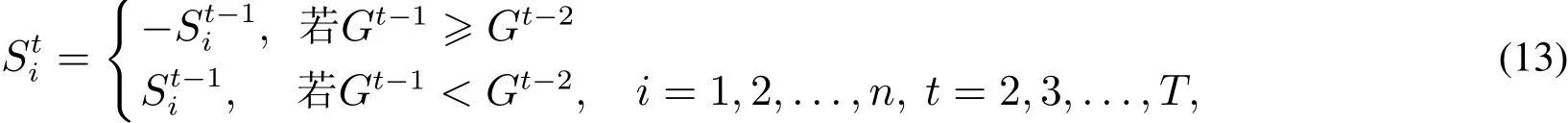
为第t轮供应商i交货期的变化趋势,其中Gt-1是第t-1轮投标后的目标值.此时,则采购商对供应商交货期dti的决策为式(12).

3.3.3基于总目标值的带有随机的交货期让步策略

策略2根据整体目标值决策交货期,而不是根据不同供应商不同目标值的偏差决策交货期,因此提出策略2的改进策略,即基于总目标值的带有随机的交货期让步策略,记为策略3.策略3的基本思想是,当本轮的分配量大于上一轮的分配量时,以较大的概率保持交货期不变,以较小的概率使交货期变化;否则以较小的概率保持交货期不变,以较大的概率使交货期变化.具体描述如下.

第一轮的交货期由式(11)—式(12)确定,此后(t≥2)交货期的变化趋势由式(13)确定,同时采购商根据供应商的不同情况确定交货期dti的让步策略为

其中γ1,γ2,υ1,υ2为参数,且γ1,υ1,υ2＞0.5,γ2＜0.5.式(14)表明若本轮的分配量大于上一轮的分配量或等于最大供应量,则以较大的概率γ1保持交货期不变,以较小的概率1-γ1变化交货期,具体为以较大的概率υ1按照目标值减小的方向定交货期,以较小的概率1-υ1按照目标值增加的方向定交货期;否则以较小的概率γ2保持交货期不变,以较大的概率1-γ2变化交货期,具体为以较大的概率υ2按照目标值增加的方向定交货期,以较小的概率1-υ2按照目标值减小的方向定交货期.对于所求的交货期,若dti/∈Di或dti＜d0,则保持上一轮的交货期.

3.4终止准则

设定到达最大拍卖轮次(T=50)或连续5次协商结果一致为协商终止准则.本文上层模型(TM)是采购商的分配策略,用于决策最优分配量,并不是每一轮最终成交情况,而实际成交的目标值是在本轮协商完成以后确定的.定义[x]+=max{x,0},则第t轮投标后的目标值为

4　集中式决策模型

为了分析所提方法的有效性,下面考虑集中式决策模型,即采购商和供应商之间信息是对称的.此时,采购商只需建立如下的集中式决策模型(CM).

上述各式中符号含义如下:

xi为0–1决策变量,若选择供应商i则为1,否则为0;

qi为整数决策变量,分配给供应商i的分配量;

di为决策变量,供应商i的交货期;

c+0为实际采购费用与目标费用的偏差,c+0≥0;

pi(qi,di)为供应商i对应于批量和交货期的最低报价,不失一般性,设pi(qi,di)为供应商的成本.

集中式决策模型(CM)与上层决策模型(TM)的区别在于:(TM)模型中采购商需要根据供应商上一轮的报价决策下一轮的最优分配量,同时需要通过不同的让步策略确定最终的交货期,而(CM)模型中所有成本和交货期的信息均已知,采购商只需要求解(CM)模型就可以确定最优分配量和最优交货期.

5　数值算例

为说明基于协商的多轮逆向拍卖机制和所提三种交货期让步策略的可行性和有效性,下面通过数值算例进行对比分析.首先通过比较三种策略的投标值和交易值说明所提三种让步策略的收敛过程,进而说明所提策略的有效性;其次通过随机产生的50组数值算例将三种策略与集中决策结果进行对比分析,说明基于总目标值的带有随机的交货期让步策略好于另外两种策略,但由于信息不对称,仍无法达到集中式决策的效果;最后通过参数分析说明所提策略具有鲁棒性.

5.1交货期让步策略分析

例1假设采购方的需求总量Q=1 500,采购预算为c0=7 500元,期望交货时间为d0=2天,两个权重系数分别设置为wc=0.7和wd=0.3,初始量设置为q=200,d=2.有N=10个供应商参与竞标,供应商的成本是私有信息.每家供应商为获得更多利润,开始都不以最低价格进行报价,此后通过竞争均以α=0.9的倍数进行降价,降价概率为λ1=0.3,λ2=0.7.

采用C++语言对策略1进行仿真,得每一轮的投标结果和实际交易结果曲线,如图2所示.

图2　策略1投标值与交易值对比Fig.2　The comparison of bid value and deal value based on strategy 1

由图2可知,对于策略1而言,前4轮拍卖的目标值连续下降,这是由于供应商降价对目标值的影响抵消了交货期变化带来的影响.当拍卖进行到第22轮时具有最佳的协商效果,目标达到最小值0.755 627,交易值不再变化,而投标值由于交货期的变化而往复交替波动.仿真结果表明所提让步策略的可行性和有效性,但在信息已知的情况下采购商的最优目标值为0.528 313,远远小于策略1的目标值.

对于例1,用C++对策略2进行仿真,得每一轮的投标结果和实际交易结果曲线,如图3所示.

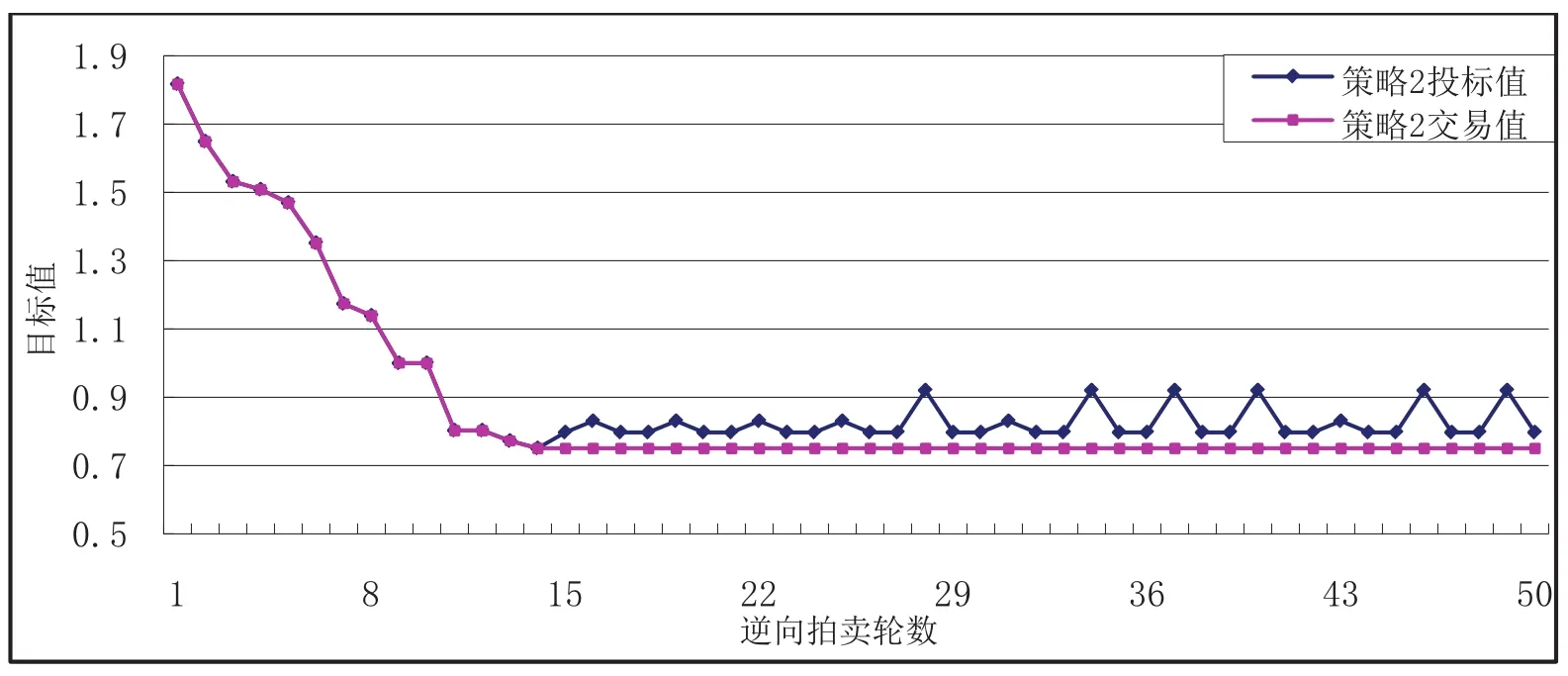
图3　策略2投标值与交易值对比Fig.3　The comparison of bid value and deal value based on strategy 2

由图3可知策略2前14轮拍卖目标值连续下降,并在第14轮时达到最小0.750 84,目标值略小于策略1.这是由于策略2搜索交货期的范围比策略1大,可以沿着目标值下降的方向寻找交货期.此外,策略1的投标值曲线由于交货期的变化而往复交替变化,而策略2的投标值曲线则会保持1轮再变化,这是由于当交货期沿着交货期减小的方向变化且实际交货期小于期望交货期时,本轮的交货期与上一轮保持一致,且报价已经降到最低.仿真结果表明策略2的可行性和有效性,但此时目标值仍比信息已知的情况大.

令γ1=0.7,γ2=0.3,υ1=0.7,υ2=0.7.对于例1,用C++对策略3进行仿真,得每一轮的投标结果和实际交易结果曲线,如图4所示.

由图4可知策略3前5轮的目标值持续下降,且在第22轮目标达到最小值0.592 393,其目标值远好于策略2.这是由于策略3对交货期的寻找范围比策略2大,且在第26轮时达到协商终止条件,整个逆向拍卖过程结束.仿真结果表明所提让步策略的可行性和有效性,但是此时的目标值与信息已知情况下的目标值0.528 313仍有一定的差距.存在这种差距的主要原因是信息不对称造成的.

图4　策略3投标值与交易值对比Fig.4　The comparison of bid value and deal value based on strategy 3

5.2交货期让步策略对比分析

为了进一步比较策略1、策略2和策略3,随机产生50组10个供应商的成本信息的数值算例,对其进行仿真.令πjk表示第j个策略第k组算例的最终结果,πk表示完全信息下第k组算例的最优值,其中j= 1,2,3且k=1,2,...,50,则三种让步策略的评价准则定义为

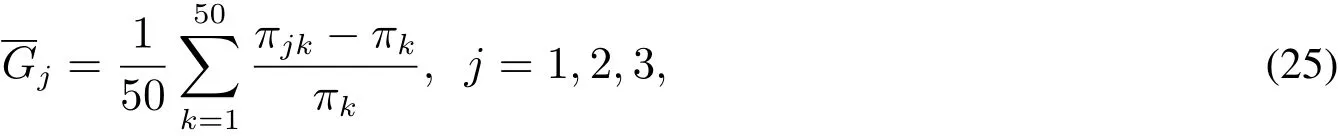
式(25)表示对于每个策略而言50组算例的平均偏差率,偏差率越小说明所提让步策略的最终结果与完全信息下的最优值越接近.

为了获得每个策略的最优参数组合,需要对初始启动量和让步策略中的参数进行测试.参数测试的具体步骤为:首先,固定交货期初始值,测试初始分配量;其次,固定测得的较好的初始分配量,测试初始交货期;最后,固定初始交货期和初始分配量,测试策略3中的随机概率.按照以上三个步骤可以获得每个策略的最优参数组合如下:策略1的最优参数组合为q0=400,d0=4;策略2的最优参数组合为q0=400, d0=5;策略3的最优参数组合为q0=500,d0=4,γ1=0.8,γ2=0.4,υ1=0.7,υ2=0.7.

在上述参数组合下,用C++对50组算例进行仿真,结果如图5所示.

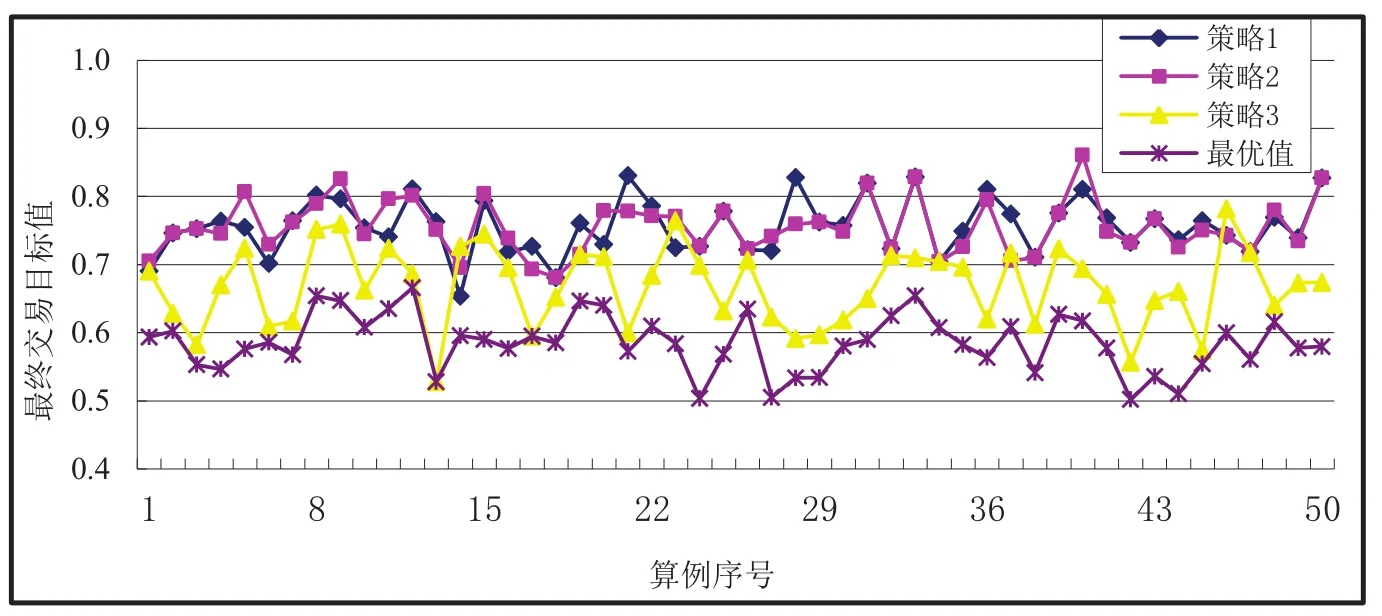
图5　三种让步策略及集中式决策结果对比分析Fig.5　The comparison of three concession strategies and the results of centralized decision-making

由图5可知策略3好于策略1和策略2且策略2略好于策略1,说明在不完全信息下采用扩大交货期寻找范围的让步策略能找到更接近最优值的解.此外,由策略1、策略2和策略3所求得的50组算例的平均偏差率分别为0.298 305,0.297 281和0.143 776,且从50组算例的个数对比也可以看出,策略3的目标值小于等于策略1的有47个,小于等于策略2的有47个,策略2的目标值小于等于策略1的有36个,进一步说明策略3具有最佳的协商效果.

5.3供应商决策参数对交货期让步策略的影响

为说明供应商决策参数α,λ1,λ2对不同交货期策略的影响,采用随机产生的50组算例进行仿真,分别计算α=0.9,0.8,0.7,λ1=0.5,0.3,0.7和λ1=0.5,0.7,0.3时的平均偏差率,其中λ1=λ2=0.5表示下层决策完全随机的情况,λ1=0.7,λ2=0.3表示下层决策出现反常的情况.仿真结果如表1所示.

表1　供应商决策参数对三种让步策略的影响Table 1　The impact of suppliers’decision-making parameters on three concession strategies

由表1可知供应商的降价系数对每种策略有显著的影响,即对于相同的降价概率,降价系数越小,每种策略的偏差率越小,说明竞争越激烈,供应商的降价系数越小,则其降价幅度越大,从而对采购商越有利;供应商的降价概率对每种策略的影响不显著,且在相同的参数组合下策略3好于策略2进而好于策略1,说明所提的交货期让步策略对供应商决策参数的变化具有鲁棒性.

5.4采购商权重参数对交货期让步策略的影响

为说明采购商所设置价格权重wc和交货期权重wd对交货期让步策略的影响,令α=0.9,λ1=0.3, λ2=0.7,采用50组随机算例进行仿真,在采购商更看重价格(wc=0.7,wd=0.3)、同等看重价格和交货期(wc=0.5,wd=0.5)和更看重交货期(wc=0.3,wd=0.7)的情况下,分析采购商权重参数对交货期让步策略的影响.

1)不同权重参数下三种让步策略目标值对比分析

在三种权重参数分配情况下,针对50组随机算例,分别计算三种让步策略的最终交易目标值,结果如图6所示.

由图6可知当价格权重较大时,策略3明显好于策略1和策略2;当交货期权与价格权重相当或较大时,策略1、策略2和策略3的差异不显著.这是由于采购商的目标仅与价格偏差率和交货期平均偏差率有关,当采购商交货期权重与价格权重相当或较大时,价格的偏差率占目标值的比重较小,而交货期平均偏差率占目标值的比重较大,交货期平均偏差率的大小与目标值的大小无明显差异.此时,对交货期和目标的调整机制达到相似的效果,因此三种让步策略的差异不显著.

2)不同权重参数下三种让步策略与最优值平均偏差率对比分析

为进一步说明采购商权重参数对交货期让步策略的影响,针对50组随机算例,分别计算不同权重参数下三种让步策略与最优值的平均偏差率,结果如表2所示.

表2　不同权重下三种让步策略与最优值的平均偏差率对比Table 2　The comparison of three concession strategies’average deviations with the optimal value under different weights

由表2可知当价格权重较大时,策略3明显好于策略1和策略2;当交货期权重与价格权重相当或较大时,三种让步策略的差异不显著.总体而言,策略3具有最佳的协商效果.

图6　三种让步策略不同权重下的目标值对比Fig.6　The comparison of three concession strategies’results under different weights

综上,通过对不同权重下三种让步策略目标值的对比分析和三种让步策略与最优值平均偏差率的对比分析可知,策略3对采购商权重参数的变化有较好的鲁棒性.

6　结束语

本文考虑由一个采购商和多个供应商组成的电子逆向拍卖系统.针对供应商成本信息未知且供应能力有限的考虑价格和交货期的两属性逆向拍卖机制设计问题,建立了基于协商的多轮拍卖两层分布式决策模型,提出确定交货期的三种让步策略,即基于交货期偏差的交货期让步策略、基于总目标值的交货期让步策略和基于总目标值的带有随机的交货期让步策略,并通过随机产生的50组数值算例对三种让步策略进行对比分析,结果表明:1)三种让步策略均具有可行性和有效性;2)基于总目标值的带有随机的交货期让步策略具有最佳的协商效果;3)基于总目标值的带有随机的交货期让步策略对供应商决策参数和采购商权重参数的变化均具有鲁棒性;4)供应商之间的竞争越激烈,则其降价幅度越大,对采购商越有利.

本文的研究为信息不对称环境下的考虑供应商能力的多属性电子逆向拍卖机制提供理论支持,对管理实践中不对称信息环境下的逆向拍卖机制设计与供应商选择具有一定的指导意义.本文仅考虑了价格和交货期两个属性,进一步研究可以考虑更多属性的情形,分析不完全信息下确定多个属性值时供应商决策参数对逆向拍卖机制设计的影响.

[1]Beall S,Carter C,Carter P L,et al.The Role of Reverse Auctions in Strategic Sourcing.Tempe:CAPS Rearch,2003.

[2]TeichJE,WalleniusH,WalleniusJ,etal.Amulti-attributee-auctionmechanismforprocurement:Theoreticalfoundations.European Journal of Operational Research,2006,175(1):90–100.

[3]Gattiker T F,Huang X,Schwarz J L.Negotiation,Email,and Internet reverse auctions:How sourcing mechanaisms deployed by buyers affect suppliers’trust.Journal of Operations Management,2007,25(1):184–202.

[4]Chandrashekar T S,Narahari Y,Rosa C H,et al.Auction-based mechanisms for electronic procurement.IEEE Transactions on Automation Science and Engineering,2007,4(3):297–321.

[5]Che Y K.Design competition through multidimensional auctions.RAND Journal of Economics,1993,24(4):668–680.

[6]Chen F.Auctioning supply contracts.Management Science,2007,53(10):1562–1576.

[7]Kostamis D,Beil D R,Duenyas I.Total-cost procurement auctions:Impact of suppliers’cost adjustments on auction format choice. Management Science,2009,55(12):1986–1999.

[8]Wan Z,Beil D R.RFQ auctions with supplier qualification screening.Operations Research,2009,57(4):934–949.

[9]Ray A K,Jenamani M,Mohapatra P K J.An efficient reverse auction mechanism for limited supplier base.Electronic Commerce Research and Applications,2011,10(2):170–182.

[10]Ray A K,Jenamani M,Mohapatra P K J.Supplier behavior modeling and winner determination using parallel MDP.Expert Systems with Applications,2011,38(5):4689–4697.

[11]Hohner G,Rich J,Ng E,et al.Combinatorial and quantity-discount procurement auctions benefit mars,incorporated and its suppliers. Interfaces,2003,33(1):23–35.

[12]Beil D R,Wein L M.An inverse-optimization-based auction mechanism to support a multiattribute RFQ process.Management Science,2003,49(11):1529–1545.

[13]Parkes D C,Kalagnanam J.Models for iterative multiattribute procurement auctions.Management Science,2005,51(3):435–451.

[14]Gallien J,Wein L M.A smart market for industrial procurement with capacity constraints.Management Science,2005,51(1):76–91.

[15]ChengCB.Reverseauctionwithbuyer-suppliernegotiationusingbi-leveldistributedprogramming.EuropeanJournalofOperational Research,2011,211(3):601–611.

[16]汪定伟.网上集中采购的捆绑—组合拍卖机制设计[J].系统工程学报,2011,26(6):809–816. Wang D W.Mechanism design of hybrid bundling and combination auction for centralized E-procurement.Journal of Systems Engineering,2011,26(6):809–816.(in Chinese)

[17]Kameshwaran S,Narahari Y,Rosa C H,et al.Multiattribute electronic procurement using goal programming.European Journal of Operational Research,2007,179(2):518–536.

[18]Elmaghraby W J,Katok E,Santamaría N.A laboratory investigation of rank feedback in procurement auctions.Manufacturing& Service Operations Management,2012,14(1):128–144.

Mechanism design of bi-attribute electronic reverse auction with discrete cost structure

Huang Min,Qian Xiaohu*,Jin Dongyang,Wang Xingwei
(College of Information Science and Engineering,Northeastern University;State Key Laboratory of Synthetical Automation for Process Industries(Northeastern University),Shenyang 110819,China)

In an electronic reverse auction system that consists of a single buyer and multiple potential suppliers,based on the bi-attribute mechanism design problem of discrete cost structure where cost and delivery time are suppliers’private information,a new iterative reverse auction mechanism based on negotiation theory is proposed for the buyer.A bi-level distributed decision-making model based on negotiation is constructed, and then we propose a concession strategy of delivery time based on deviation of delivery time,a concession strategy of delivery time based on overall target value and a concession strategy of delivery time with randomness based on overall target value.A numerical example is given to show the feasibility and effectiveness of the proposed strategies.Finally,the comparison between the three concession strategies is presented by randomly generated numerical examples,and the result shows that the concession strategy of delivery time with randomness based on overall target value is the best in comparison with the other two.

electronic reverse auction;mechanism design;bi-level distributed decision making model;negotiation;concession strategy of delivery time

F713.36;F224

A

1000-5781(2016)01-0088-13

10.13383/j.cnki.jse.2016.01.009

2013-07-10;

2014-06-26.

国家杰出青年科学基金资助项目(71325002;61225012);国家自然科学基金资助项目(71071028;70931001; 71021061);高等学校博士学科点专项科研基金优先发展领域资助项目(20120042130003);高等学校博士学科点专项科研基金资助项目(20110042110024);中央高校基本科研业务费资助项目(N110204003;N120104001);流程工业综合自动化国家重点实验室基础科研业务费资助项目(2013ZCX11);东北大学基本科研业务费资助项目(N130604004).

黄 敏(1968—),女,福建长乐人,博士,教授,博士生导师,研究方向:物流与供应链管理等,Email:mhuang@mail.neu.edu.cn;

钱小虎(1986—),男,江苏泰兴人,博士生,研究方向:机制设计与逆向拍卖等,Email:qian_xiaohu@126.com;

金东洋(1987—),男,河北阜城人,硕士生,研究方向:多属性电子逆向拍卖等,Email:328443742@qq.com;

王兴伟(1968—),男,辽宁盖州人,博士,教授,博士生导师,研究方向:新一代互联网等,Email:wangxw@mail.neu.edu.cn.