高钢级管道焊缝材料应力应变本构关系确定方法

张 东 刘啸奔 孔天威 杨 悦 武学健 吴 锴 张 宏

1.中国石油大学(北京)油气管道输送安全国家工程研究中心,北京,102249

2.合肥通用机械研究院有限公司国家压力容器与管道安全工程技术研究中心,合肥,230031

0 引言

长输管道作为典型的焊接结构,在焊缝区和热影响区难免会出现裂纹、未焊透、未熔合等一系列焊接缺陷[1-2]。近年来我国发生了一系列管道环焊缝失效事故,对环境及人民生命财产造成难以估计的损失[3-4]。自2008年来,以中缅管道、漠大线、陕京三线等为代表的高钢级管道(X70、X80)在建成试压和投产运行初期发生了30余起环焊缝开裂和泄漏事故[5]。国内外许多学者、机构针对环焊缝失效问题开展了大量的研究,提出了许多管道环焊缝安全评价模型[6-7],其中,现有安全评价模型多以环向全焊缝应力应变本构关系为输入。但是目前管道环焊缝的失效一般是由于轴向载荷引起的管道环向裂纹开裂,这与输入的环向材料属性是不匹配的。吴锴[8]利用数字图像相关(digital image correlation,DIC)技术对X80管道环焊缝轴向试样进行了单轴拉伸试验,测得了试样颈缩前的应力应变曲线,与环向全焊缝试样真应力应变曲线进行了对比,发现与环向试样相比,焊缝金属轴向强度明显更小。由此可知,采用环向全焊缝试样获得的应力应变本构关系来表征环焊缝的材料特性会高估环焊缝的实际承载能力。为降低管道环焊缝的失效概率,如何测定焊缝区材料轴向真实应力应变本构关系成为保障管道安全运行的关键一环。

国内外针对油气管道焊缝区材料应力应变本构关系测定问题已开展了大量的研究[9-11],主要包括半经验解析公式法、小冲杆试验和DIC技术等方法。在半经验解析公式方面,CHEN等[12]根据典型体积元等效能量原理和材料变形区域的经典空腔假设推导出一种等效能量压痕模型,基于压痕的加载部分曲线反向预测了材料单轴应力应变关系,但是该方法的预测结果与拉伸试验结果的吻合度较差。TU等[13]基于有限元方法提出了一种含缺口试样真实应力应变曲线转化为材料等效应力应变曲线的校正解析方法,但是该方法中需要实时记录试样的最小横截面积,对试验设备的要求较高,且该方法并未通过试验验证。在小冲杆试验方面,CHEN等[14]开展圆片小冲杆试验获得了载荷位移曲线,通过等效能量理论推导和有限元数值模拟相结合的方法提出了一种材料应力应变关系半经验公式,但是该方法受到小冲杆试验装置和试样尺寸的限制,尚没有一个统一的半经验关联公式。基于上述能量等效原理,刘刚等[15]采用新型长条形小冲杆试样提出了关于该试样的Chen-Cai半解析方程的4个系数,进而提出了依据长条形小冲杆试样的载荷位移曲线估算金属材料的单轴本构关系的新型试验方法,但是该估算方法结果与单轴拉伸试验结果对比存在不小的误差。ZHONG等[16]开展小冲杆试验得到了载荷位移曲线,通过数据库方法确定了Ludwik硬化本构模型的参数,该方法只能计算试样颈缩前的真实应力应变曲线,且与拉伸试验结果对比的误差不可忽略。另外还有学者利用DIC技术探究了非均质材料本构关系。DIC技术通过比较试件变形前后表面数字图像差异来实现高精度变形测量,并逐渐应用于焊缝区域的本构关系测量。REYNOLDS等[17]于1999年发表了关于使用DIC技术研究焊接区域本构关系的报告,并基于均匀应力假设对铝合金板的焊接接头进行了拉伸试验,获得了焊接区域的板材、热影响区和焊缝的力学参数。但LOCKWOOD等[18]利用有限元的方法对上述实验结果进行验证时发现,基于均匀应力假设的结果和有限元模拟存在一定误差。武旭[19]使用DIC技术并结合MTS拉伸机输出的载荷获取了X80管道母材、热影响区和焊缝区材料的应力应变关系。但是DIC技术中试样真应力是基于体积不变原理得到的,因此在试样发生颈缩后,DIC技术得到的应力应变曲线不可靠。

针对以往学者研究的不足,本文基于焊缝区含缺口圆棒单轴拉伸试验结果,通过ABAQUS非线性有限元软件对拉伸试验进行建模重构,利用贝叶斯正则化反向传播(Bayesian regularization back-propagation,BRBP)神经网络和灰狼优化算法(grey wolf optimizer,GWO)对ABAQUS中输入的真实应力应变曲线进行迭代优化反演,准确得到了焊缝区的真实应力应变本构关系。该方法弥补了现有测试高钢级管道焊缝区材料应力应变本构关系的不足,以期为高钢级管道环焊缝安全评价提供准确的应力应变本构关系,进一步保障油气管道的安全运行,具有一定的实际工程意义。

1 缺口圆棒拉伸试验

1.1 试验设计及流程

为探究高强钢管道焊缝区材料真实应力应变本构关系,本节选取中俄东线现场截取的API-5L X80管线钢某道焊口作为试验材料,该道焊口采用全自动焊工艺(熔化极气体保护实心焊丝电弧焊),未服役且不存在腐蚀等缺陷,试样取材位置焊材性能合格。以环焊缝为中间区域沿管道轴向制作带缺口圆棒试样,试样取样于环焊缝填充焊区域,试验中所有试样均为同一位置连续取样,图1所示为试样与环焊缝的相对位置关系。参考标准ASTM A370—2017《Standard Test Methods and Definitions for Mechanical Testing of Steel Products》对金属材料标准拉伸试样的尺寸设计要求,结合拉伸试验设备对试样夹持长度的硬性要求,设计了4组不同缺口类型试验,每组设置2根试样以避免试验结果的偶然性,具体试样尺寸如图2所示,其中R为试样的最大半径,R1为缺口圆的半径,R2为试样的最小半径,h为缺口圆圆心与试样表面的距离,试样夹持段为40 mm,引伸计测量区长度为20 mm,试样最大截面直径为10 mm,其余变化尺寸见表1。

表1 各组试样尺寸详细表

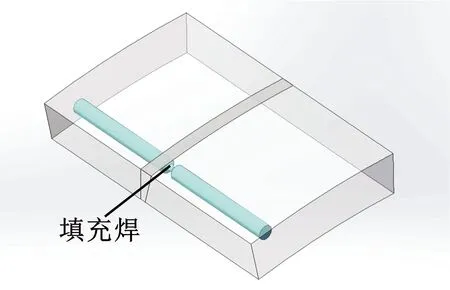
图1 试样与环焊缝的相对位置示意图

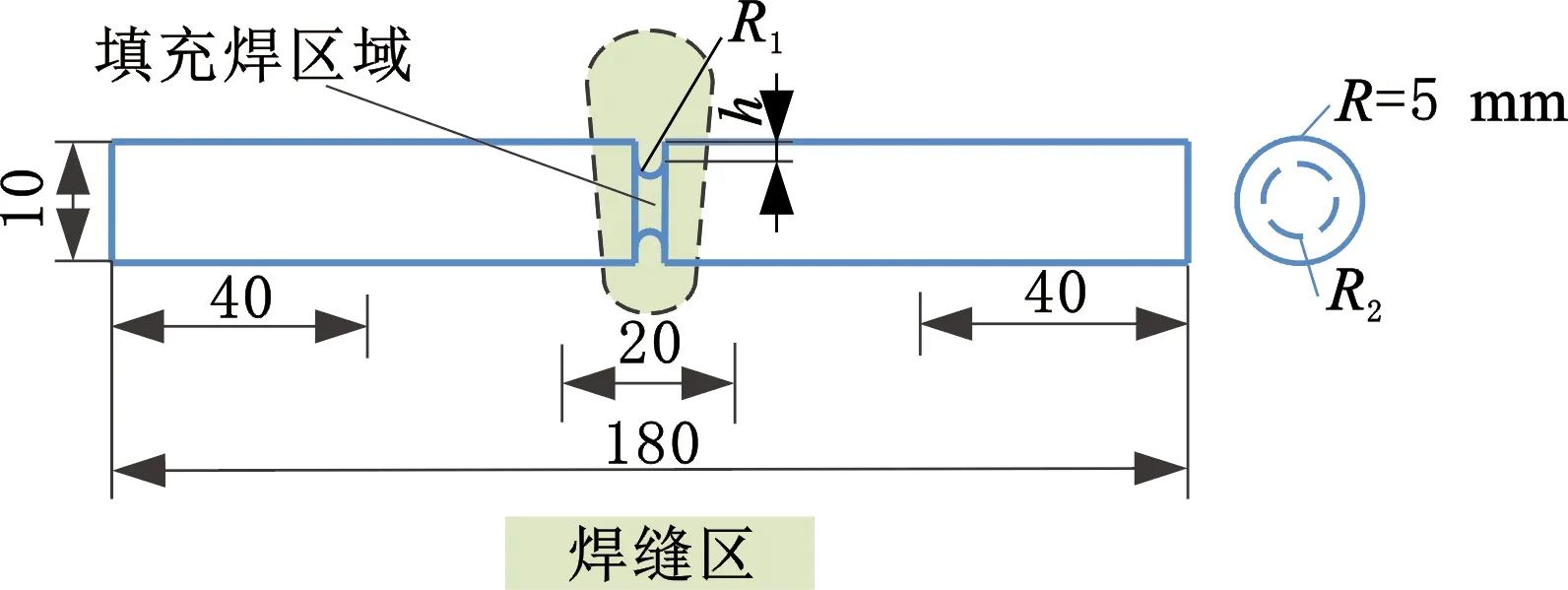
图2 试样尺寸示意图

采用GNT200微机控制电子万能试验机开展拉伸试验,选择合适的夹具,将处理好的试样装夹在试验机液压夹具上,夹持段取圆棒试样两端各40 mm,试验温度为室温20 ℃,引伸计初始长度为20 mm,量程为5 mm。试验采用位移控制的加载方式,为保证试验处于准静态拉伸状态,加载速率保持为0.5 mm/min,试验加载至试样完全断裂,试验设备与加载方式如图3所示。

(a)试验设备 (b)试样加载

1.2 试验结果

通过焊缝区含缺口圆棒单轴拉伸试验得到了4组不同缺口尺寸试样的载荷-位移曲线。A1-A2试样、B1-B2试样的载荷位移曲线分别见图4a、图4b,可以发现A组试验曲线在位移为0.4 mm之前吻合度较好,在位移为0.4 mm之后A1试样曲线存在明显的转折,该转折点在宏观上表现为试样起裂,A2试样起裂位移为0.7 mm,A组两根试样的起裂位移不同的原因在于焊缝区域材料的局部差异性。试样起裂后涉及到材料损伤问题,需要在模型中引入GTN等损伤本构模型,这不在本方法的讨论范围内。B组试验存在同样的现象,B1试样起裂位移为1.0 mm,B2试样起裂位移为0.7 mm,A组与B组试验起裂点位移不同的原因在于试样的最小截面半径不同。C1-C2试样、D1-D2试样的载荷-位移曲线分别见图4c、图4d,可以发现C组、D组试验曲线在弹性阶段基本一致,当试样局部区域进入塑性阶段后,D1-D2试样曲线出现了明显的差异,相较而言,C1-C2试样曲线差异较小,但仍存在一定的差异性,其原因将在下文进一步讨论。

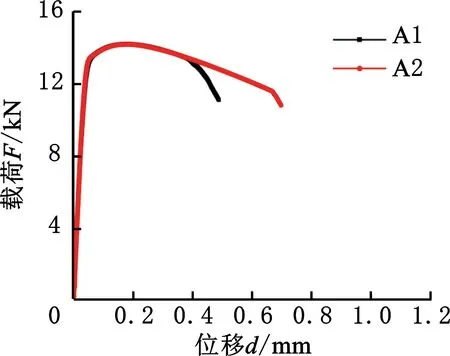
(a)试验A

观察4组完成拉伸试验的圆棒试样缺口宏观形貌(图5)可以发现,A组、B组试样的变形集中在缺口位置,缺口外区域没有发生明显的塑性变形;而C组、D组试样除缺口位置发生集中变形外,缺口附近的母材区也发生了明显的颈缩现象,且D组试样颈缩现象较C组更为明显。由试样尺寸可知,C组试样的最小截面直径为7 mm,D组试样的最小截面直径为8 mm,即最小截面面积越大,颈缩现象越明显。同时,上述试验宏观形貌也与各组试验载荷-位移曲线的差异性结论相一致。考虑到该缺口圆棒试样为焊缝与母材组合而成,而该环焊缝材料处于高强匹配状态,即焊缝材料屈服强度高于母材的屈服强度,因此,当焊缝区最小截面与母材最大截面的面积之比大于一定值时,母材区域将会发生颈缩现象。并且,随着最小截面面积的增大,母材的颈缩现象会逐渐明显,直至颈缩完全出现在母材区域。

图5 试样宏观形貌图

2 有限元模型

2.1 边界与网格

由于无法通过试验数据得到准确的焊缝材料应力应变本构关系,因此,采用非线性有限元软件ABAQUS建立含缺口圆棒单轴拉伸数值仿真模型对上述试验进行重构反演,考虑到模型的对称性以及后续优化反演算法的效率,该模型采用二维轴对称模型。模型尺寸与试验试样尺寸相同,对缺口右端位置施加YSYMM对称约束,对模型夹持区施加Y方向的位移,约束X方向的平动自由度以及UR3方向的转动自由度。在距离模型右端10 mm处截面设置一个点集,起到试验中引伸计的作用(图6)。

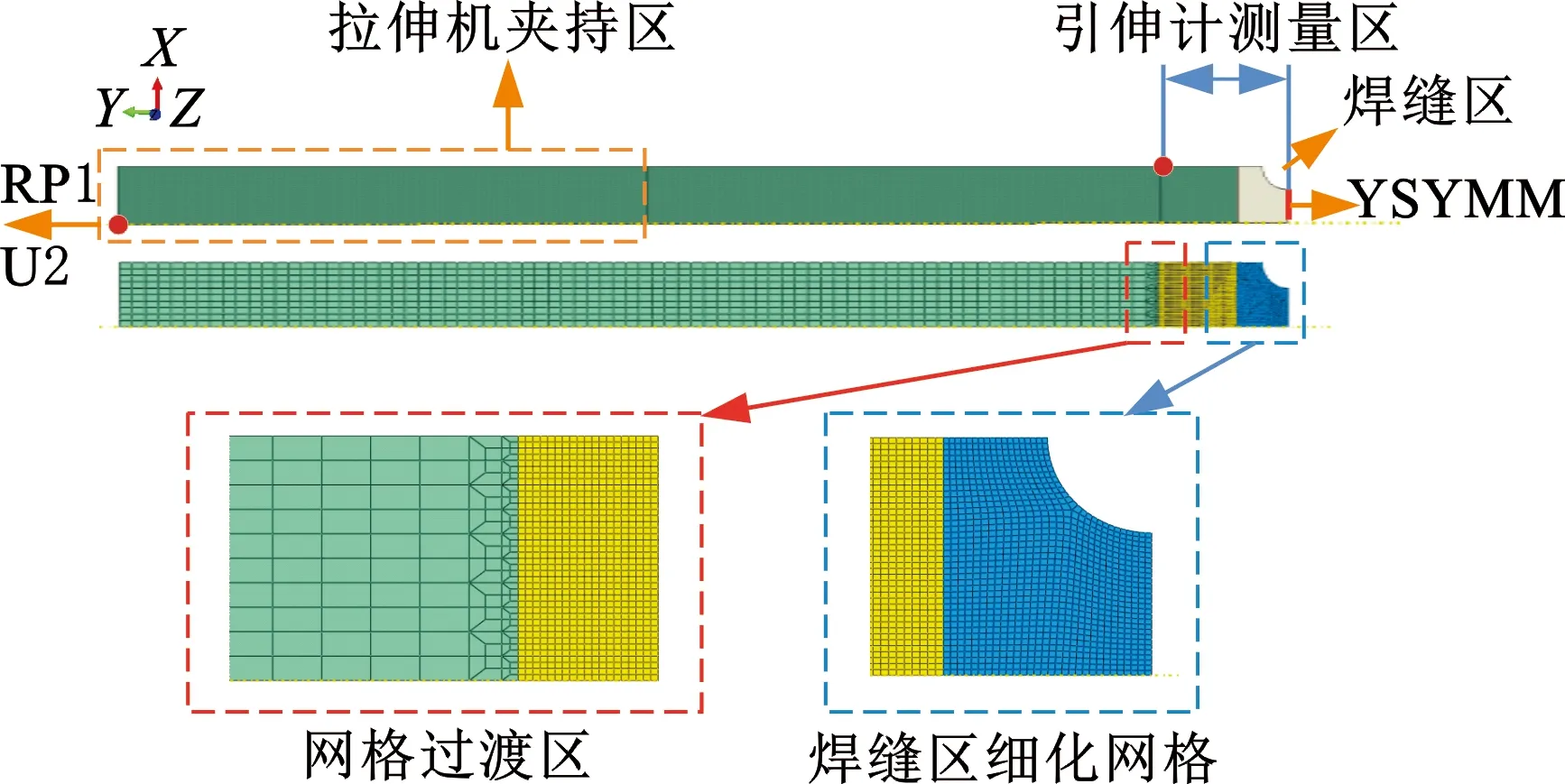
图6 有限元模型示意图

模型单元采用二次减缩积分单元(CAX8R),对试样模型进行网格划分时,考虑到缺口位置应变集中的现象,同时为了提高模型的计算准确度与收敛性,因此在缺口位置与引伸计测量区域对网格进行加密处理,设定网格单元的尺寸为0.1 mm。采用Y字形过渡网格来减少模型网格数量(图6),模型其余部分网格尺寸为1 mm,整个模型包含的单元数量为3163个。

2.2 材料本构模型

管线钢材料的应力应变本构模型在工程中存在多种描述方式,在各向同性硬化情况下,通常采用基于幂指数函数的硬化模型。NIMA等[20]使用Hollomon模型对管材的本构模型进行表征,发现幂律模型与管材的真实本构模型较为相近,但该本构模型描述中缺乏弹性模量、屈服强度等管线钢典型参数。JIANG等[21]、ZHANG等[22]采用Ramberg-Osgood(RO)模型来描述管线钢的真应力应变本构模型,该模型将弹性模量、屈服强度纳入本构模型中,并通过试验数据与RO模型数据对比验证了本构模型的准确性。

基于上述分析,本文采用油气管道设计与评价领域常用的RO模型来描述材料的应力应变本构关系,其表达式如下:

(1)

式中,ε为管材应变;σ为管材应力,MPa;E为弹性模量,MPa;α为屈服偏移量;n为硬化指数;σy为管材屈服强度,MPa。

针对母材区域本构模型,当焊缝区最小截面与母材区最大截面的面积之比小于一定临界值时,母材区域等效应力始终小于材料屈服强度,即母材区域总是处于弹性阶段。该比例临界值与材料的匹配系数有关,匹配系数越小,该比例临界值越接近1。由于本文以焊缝区材料本构关系为研究目标,因此需要保证模型的变形集中在焊缝缺口区域,防止母材区域发生塑性变形,影响后续反演方法的准确性。综上所述,本文对母材材料仅赋予纯弹性属性,其中弹性模量取经验值2×105MPa,泊松比取0.3。

针对焊缝区域本构模型,由于缺口的存在,该区域存在应力、应变集中现象,因此该区域塑性数据影响着整个模型结果的准确程度。由式(1)可知该本构模型由E、α、n、σy4个变量决定,其中弹性模量E取经验值2×105MPa,其余3个变量均属于未知参量,3个变量的不同组合形成了不同的塑性数据,因此,确定焊缝区应力应变本构关系的关键问题就是寻找3个变量的最优组合。

3 焊缝区材料本构关系反演方法

3.1 BRBP神经网络与GWO算法介绍

反向传播(back propagation,BP)神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络。BP神经网络无论在网络理论还是在性能方面都已比较成熟,它突出的优点就是具有很强的非线性映射能力和柔性的网络结构。网络的中间层数、各层的神经元个数可根据具体情况任意设定,并且随着结构的差异其性能也有所不同[23-25]。但是BP神经网络也存在学习速度慢、容易陷入局部极小值等缺点。为了克服BP神经网络的上述问题,贝叶斯正则化BP(BRBP)模型是在BP神经网络基础上引入贝叶斯正则化规则的模型,可提高网络的训练速度以及泛化性能,修改后的目标函数加入了神经网络权值,其表达式如下:

Ft=λEW+βED

(2)

其中,EW为网络权重平方和;ED为网络响应与目标值的残差平方和;λ、β为目标函数正则化系数,其大小会直接影响到网络的拟合效果。若λ≪β,则通过调节网络规模可以得到理想的训练误差,但可能会出现训练过度的情况,导致产生过拟合现象;若λ≫β,则连接权重可能会大规模降低,使得网络规模减小并简化,进而出现欠拟合现象,导致训练误差达不到预期效果[26-27]。

为了得到最优的λ和β,基于贝叶斯分析方法,认为网络权重和训练样本的先验分布均服从高斯分布。基于后验函数最大化的原则,对BR性能函数进行求解,得到最优的正则化系数λ*和β*,其表达式分别如下:

(3)

(4)

式中,φ为有效权值个数,反映网络实际规模;m为神经网络训练样本集的数目;ω*为神经网络性能指数最小时的权值矩阵[28]。

灰狼优化算法(GWO)是一种基于灰狼捕食猎物行为开发的群智能优化算法,它具有较强的收敛性能、参数少、易实现等特点,近年来受到了学者们的广泛关注,已被成功地应用到了车间调度、参数优化、图像分类等领域中[29]。整个狼群按照适应度函数值由大到小依次分为α狼、β狼、δ狼和ω狼四个社会等级。狼群捕猎分为包围、捕猎、攻击三个过程。在寻优过程中,灰狼个体与猎物之间的距离以及灰狼位置的更新可分别表示为

D=|CXP(t)-X(t)|

(5)

X(t+1)=XP(t)-DA

(6)

其中,D为灰狼与猎物间的距离;t为当前迭代次数;XP、X分别为猎物的位置向量和灰狼的位置向量;A、C为系数向量,其计算公式分别如下:

A=2μr1-μ

(7)

C=2r2

(8)

其中,μ为收敛因子,随着迭代次数从2线性减小到0;r1、r2为[0,1]区间的随机向量。经过移动后灰狼群向α狼移动,移动方向由自身位置和随机向量C决定,移动步长由灰狼与猎物的距离和系数向量A决定,系数向量A与C的存在很好地避免GWO算法陷入局部最优[30],图7为灰狼位置更新示意图。

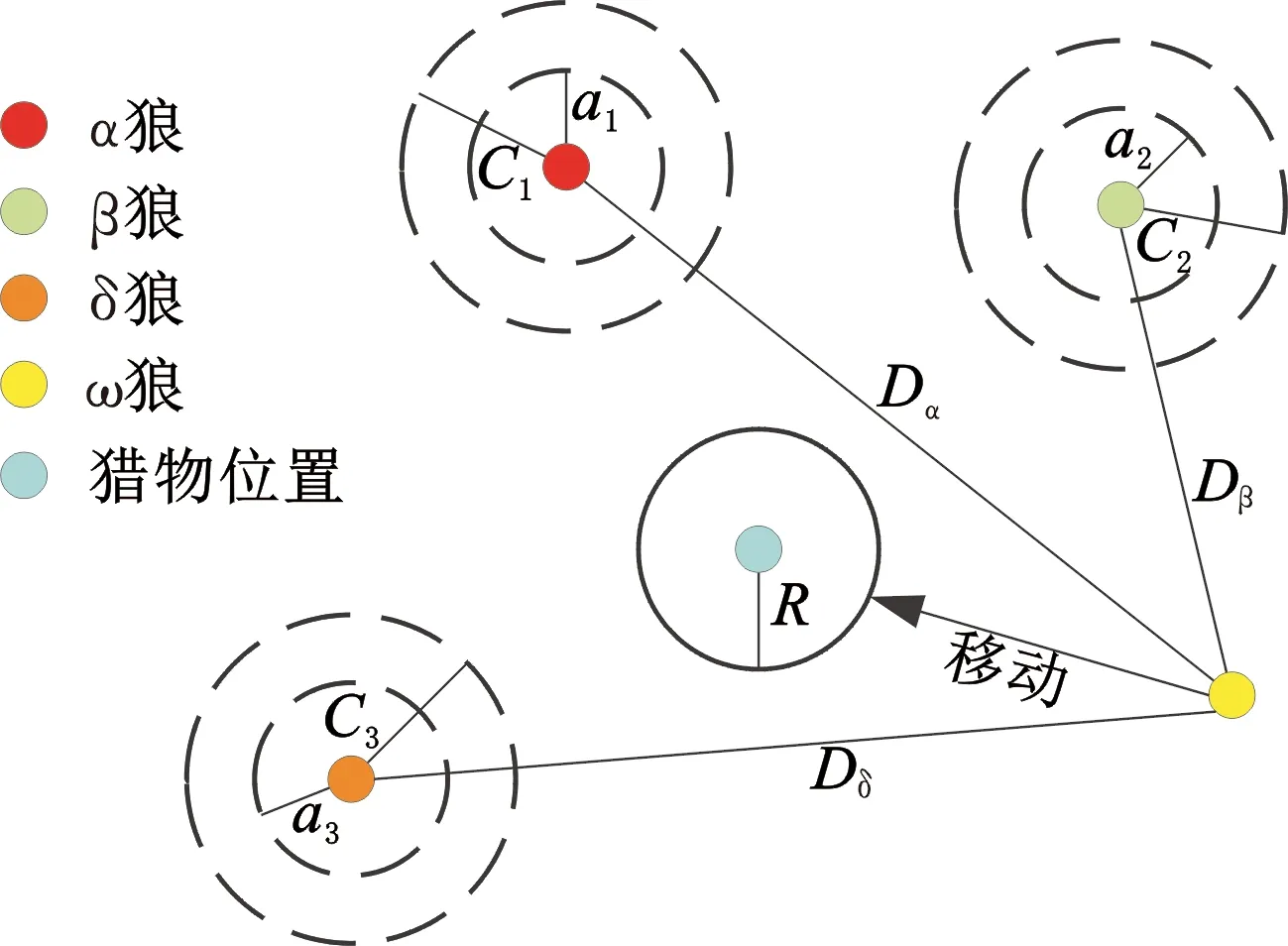
图7 灰狼位置更新图

3.2 反演流程及结果

为探究焊缝区材料的真实应力应变本构关系,本文基于MATLAB-PYTHON-ABAQUS开展联合仿真。以MATLAB为主程序平台,利用PYTHON对ABAQUS有限元模型进行参数化计算以及后处理,以Excel为数据载体实现三个软件间的数据无损精准传输,从而成功地将三个功能强大的计算软件有机地形成一种智能交互关联关系,真正做到一键操作即可自动建模、自动提取结果、自动开展优化反演分析,显著提高了研究人员的工作效率,提高了计算结果的精度与准确性,反演流程如图8所示。

图8 反演流程图

基于含缺口圆棒单轴拉伸试验数据与有限元模型开展了焊缝区应力应变本构关系反演分析。由式(1)可知RO本构模型包含三个可变参数(σy,α,n),吴锴[8]利用DIC技术分别对中俄东线X80管道环焊缝轴向和环向屈服强度进行了测试,得到材料的屈服强度在630 MPa左右。武旭[19]同样采用DIC技术对X80管道环焊缝真应力应变曲线进行了测定,通过拟合方法得到了RO本构模型参数,参数α的范围为0.62～0.82,参数n的范围为9.2～10.2,屈服强度σy的范围为542～579 MPa,但是该研究指出其试验材料为低强匹配材料。考虑到本次拉伸试验材料为高强匹配材料,结合国家标准GB/T 50470—2017附录C中各钢级的参数取值以及各文献中得到的RO本构模型参数取值,保守考虑后基本可以确定参数α、n的取值范围。由于笔者前期对该道焊口开展了全焊缝环向圆棒单轴拉伸试验,可知该材料的环向屈服强度约为675 MPa,考虑到环焊缝材料轴向屈服强度通常小于环向屈服强度,基于此假定轴向屈服强度范围为600～700 MPa。其中5组基础工况参数取值为基于经验与文献的自主取值,具体如表2所示。

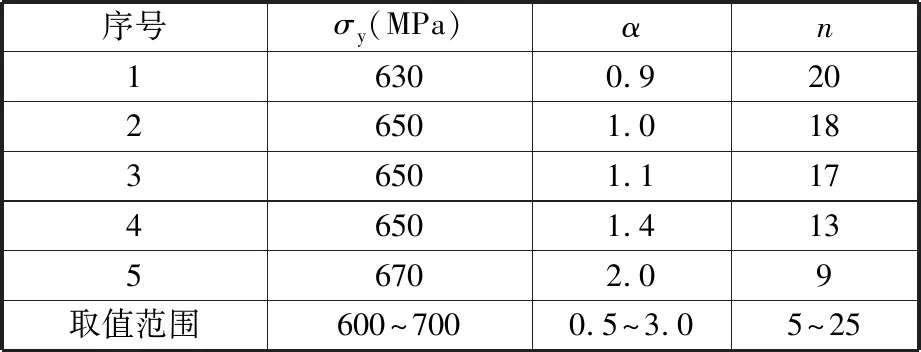
表2 RO本构模型初始参数设置及取值范围

选择B1组试验载荷位移曲线作为目标,将0.05～0.9 mm区间的曲线均分为24段即可生成25个关键点(图9)。利用非线性有限元软件ABAQUS分别对5组RO本构模型开展计算得到相应的5组载荷-位移曲线,利用插值方法进一步得到5组载荷-位移曲线的关键点信息。以RO本构模型参数为自变量,以每条载荷-位移曲线25个关键点的载荷数据信息为因变量,采用BRBP神经网络进行回归训练,训练集取80%,测试集取20%,允许误差为10-4,迭代次数设置为2500,隐含层数目为20,从而得到RO本构模型参数与关键点的映射函数关系。

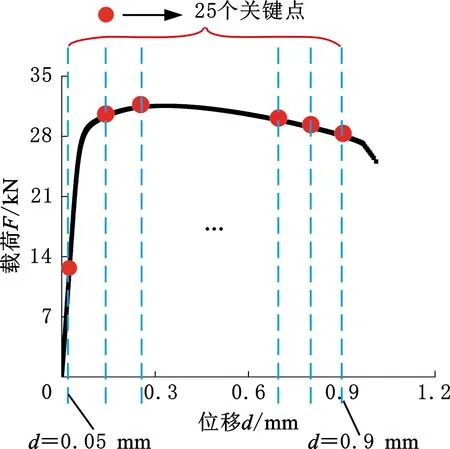
图9 25个关键点选取示意图

通过BRBP神经网络拟合映射函数与拉伸试验数据构建相对均方误差(relative mean square error,RMSE),其表达式如下:

(9)

其中,Fsim为25个关键点处神经网络输出的载荷数据,Fexp为25个关键点处试验曲线中的载荷数据。以相对均方误差为GWO算法的适应度函数开展优化分析,其中,算法灰狼个数为40,允许误差为10-4,最大迭代次数为100。以小于允许误差和达到最大迭代次数两个指标为优化算法停止的条件,两个指标满足其中一个即跳出优化算法。

算法经过18次循环,满足了算法的允许误差目标,图10所示为试验载荷位移曲线与本文反演方法得到的载荷位移曲线对比,可以发现二者无明显的差异,相对误差仅为0.26%。通过上述优化反演方法得到的最优应力应变本构曲线及参数组合如图11所示。

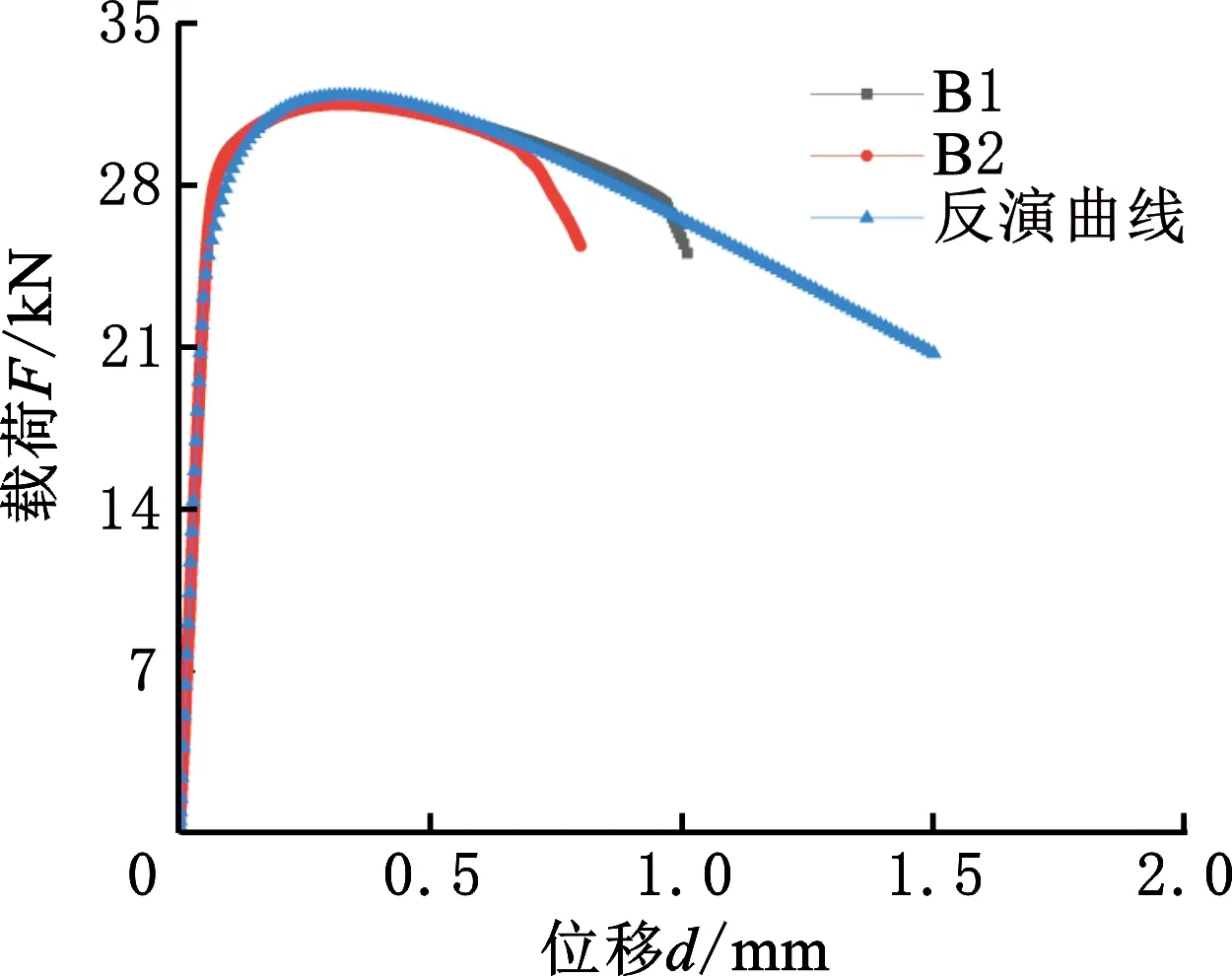
图10 B组试验曲线与反演曲线对比

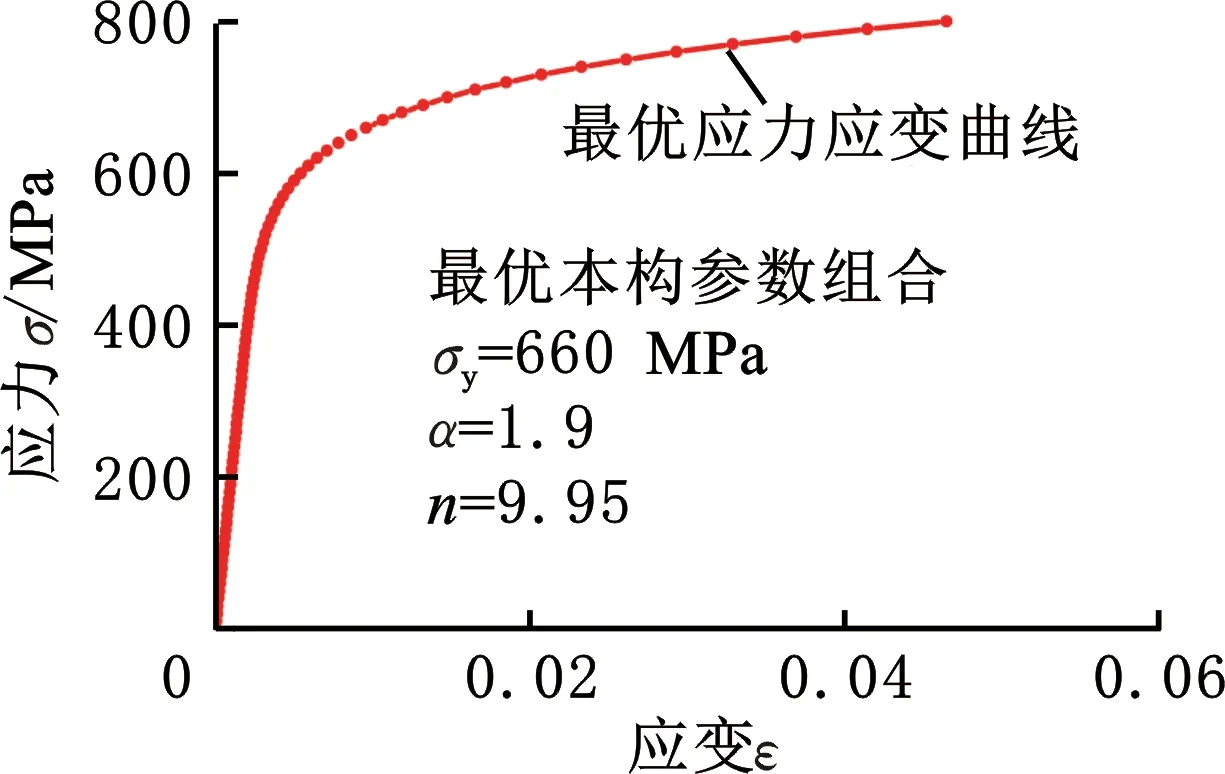
图11 最优应力应变曲线

分别提取位移d=0.3 mm、0.6 mm、0.9 mm、1.2 mm条件下试样的等效塑性应变云图(图12),可以发现塑性应变主要集中在试样缺口处,最大等效塑性应变出现在试样最小截面的外表面处。由于母材区域应力在拉伸过程中一直未达到材料屈服强度,因此,在采用本文反演方法过程中,若缺乏母材的材料应力应变本构关系,则可将母材本构关系视为纯弹性。但是当试样最小截面直径与最大截面直径之比超过一临界值时,母材区域会发生明显的塑性变形,因此在未知母材本构关系的情况下利用本方法得到的结果是不可靠的,本文试验C、试验D即出现了该现象。

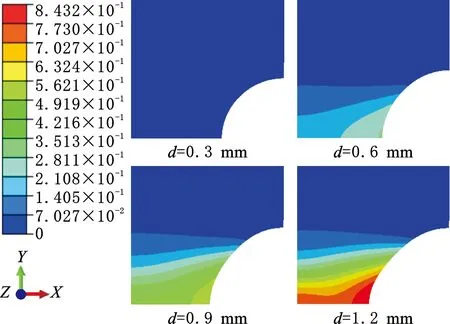
图12 加载历程中试样等效塑性应变分布云图

3.3 结果验证

为验证焊缝区材料本构关系反演结果的准确性,建立与A组试样尺寸一致的有限元模型,将基于B组试验反演得到的最优本构模型参数输入到有限元模型中,基于母材材料不变开展数值仿真计算并提取载荷-位移曲线。图13为A组试验曲线与有限元曲线的对比图,可以发现,在弹性阶段两组曲线吻合度较高,在塑性阶段两组曲线存在一定误差,相对误差为0.81%,该误差可能由试样缺口加工尺寸的微小变化引起,且在工程可接受范围内。

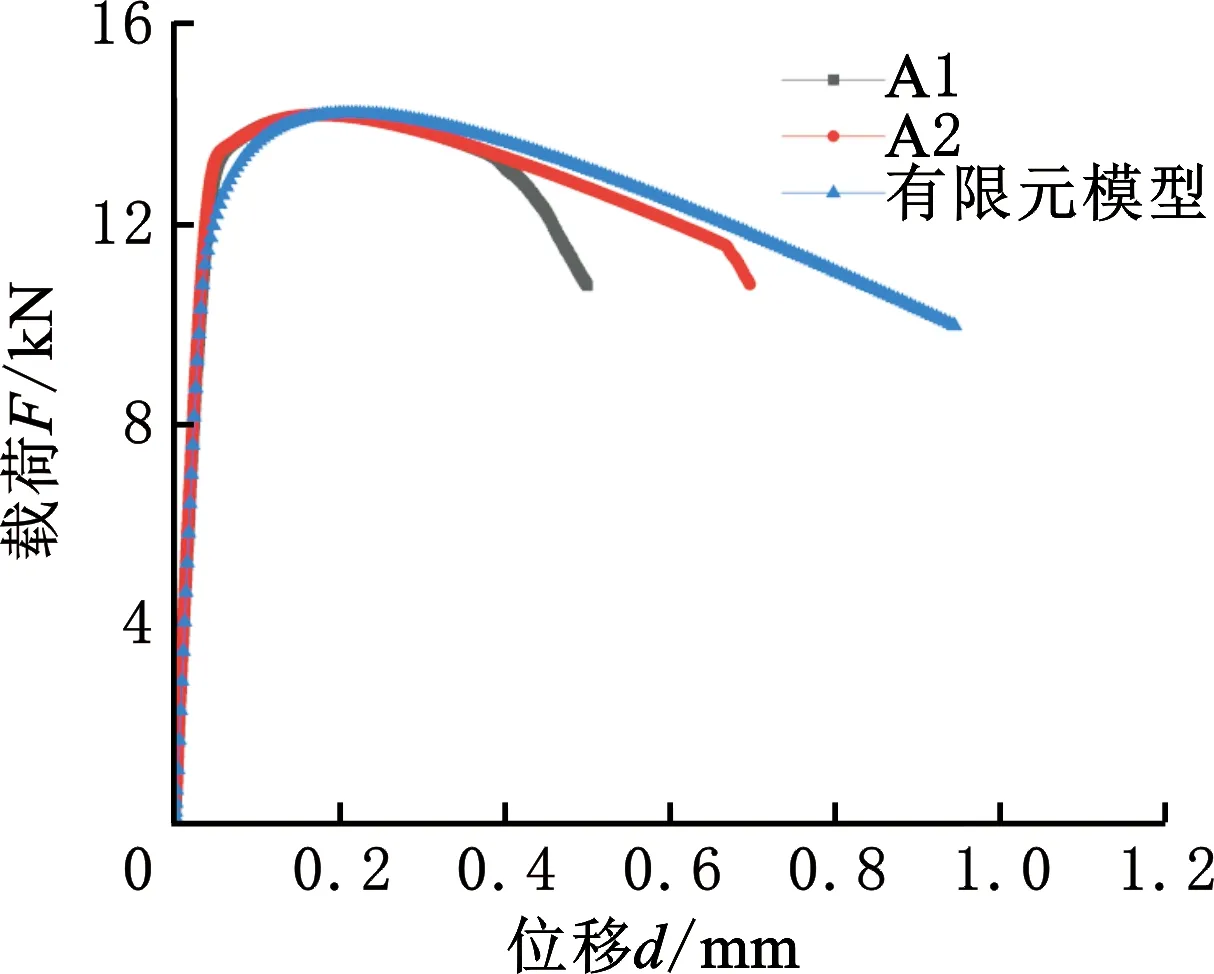
图13 A组试验与有限元曲线对比

4 结论

本文基于MATLAB-PYTHON-ABAQUS联合仿真提出了一种通用的管道焊缝区材料应力应变本构关系优化反演方法。开展了4组不同缺口尺寸的拉伸试验,得到了各试样的载荷-位移曲线,利用贝叶斯正则化反向传播(BRBP)神经网络和灰狼优化算法(GWO)得到了焊缝区材料的真实应力应变本构关系。具体结论如下:

(1)针对焊缝区含缺口圆棒试样,在拉伸过程中,需要确保母材区域不发生塑性变形,这与试样的尺寸和材料强度匹配相关。在本文开展的4组试验中,C组、D组试验母材区发生了明显的颈缩现象。

(2)以B组试验曲线为优化目标开展优化反演,相对误差为0.26%;将B组得到的最优本构模型作为A组有限元模型的输入,计算得到的载荷-位移曲线与A组试验得到的曲线的相对误差为0.81%,充分验证了反演方法的准确性。

(3)本文提出的思路同样适用于均质金属材料大应变范围应力应变曲线的测定。