“裁出”与“拼成”

蒋成法

问题1：把一张长15厘米、宽9厘米的长方形纸裁成同样大的正方形。如果要求纸没有剩余，那么裁出的正方形边长最大是多少厘米？一共可以裁出多少个这样的正方形？

思路点睛：细读题目，我们可以发现，裁出的小正方形的边长应该既是15的因数，又是9的因数，也就是15和9的公因数；又因为要求边长最大，所以本题其实就是求15和9的最大公因数。

15和9的最大公因数是3，因此裁出的小正方形的边长就是3厘米。

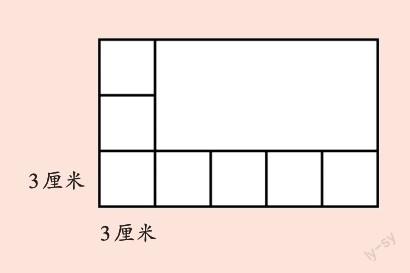
画图分一分，可以发现长15厘米里有5个3厘米，即长边可以分出5个，同理宽边可以分出3个，把两个数相乘，得到5×3=15，即一共可以裁出15个这样的正方形。

问题2：用若干个长45厘米、宽30厘米的长方形拼成一个大正方形。拼成的正方形边长最小是多少厘米？一共需要多少个这样的长方形才能拼成？

思路点睛：和前面的问题正好相反，要拼成一个大正方形，应该是求45和30的最小公倍数。45和30的最小公倍数是90，那么拼成的正方形边长最小是90厘米。90÷45=2，90÷30=3，2×3=6，即一共需要6个这样的长方形。如下图：

對比上面的两种情况，你有什么发现呢？以后遇到这样的问题，你知道怎么解答了吗？