联系推导过程
2023-09-17 19:28:14吉继红
小学生学习指导·高年级 2023年2期
吉继红
同学们一定还记得把圆柱切割成若干等份,然后拼成一个近似长方体的过程吧!在这个过程中,圆柱的底面积不变,高不变,体积也不变,但是表面积变了。
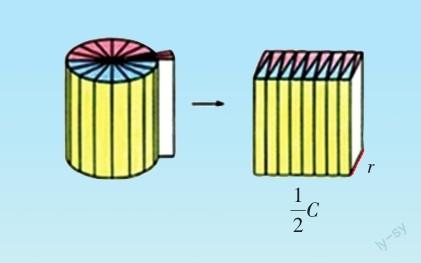
从上图可以看出,拼成的近似长方体的长等于圆柱底面周长的一半,宽等于圆柱的底面半径,高就是圆柱的高。长方体前面的面积相当于圆柱侧面积的一半,而长方体表面积增加的部分就是长方体的左、右两个面。
理解了上面的知识,我们就可以解答下面的问题了。
问题:把底面直径为8厘米的圆柱切成若干等份,拼成一个近似的长方体,长方体的表面积比圆柱的表面积增加了80平方厘米,这个圆柱的体积是多少平方厘米?
思路点睛:题中已经给出了圆柱的底面直径,要求体积,还需要知道圆柱的高,由此問题就转化成了求圆柱的高。
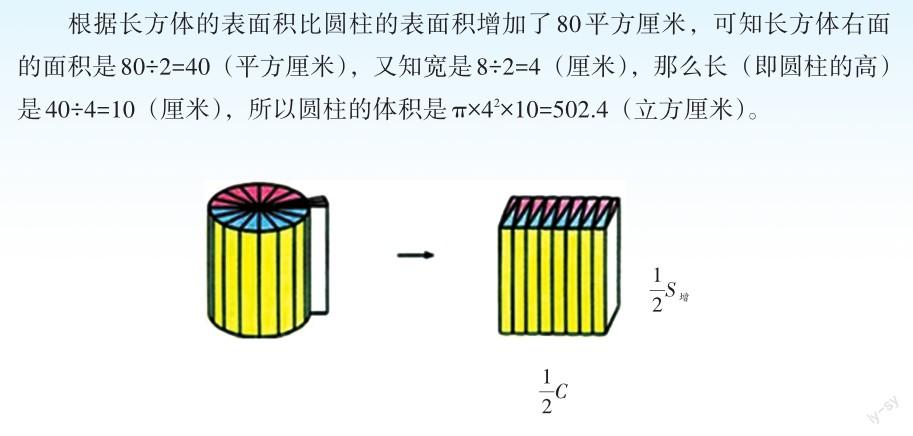
从图中还可以看出,长方体的长是底面周长的一半,即8π÷2=12.56(厘米),右面的面积是80÷2=40(平方厘米),那么用右面的面积×长,同样能得到圆柱的体积,即40×4π=502.4(立方厘米)。
我们换个角度来解答同样可行。因此,学会从不同角度来思考问题,可以使我们的解答更灵活、更便捷。
猜你喜欢
数学小灵通(1-2年级)(2024年2期)2024-05-14 09:23:04
小学生学习指导(高年级)(2023年6期)2023-07-04 01:38:14
小学生学习指导·高年级(2022年2期)2022-02-16 17:51:39
小学生学习指导·低年级(2021年6期)2021-09-10 18:19:54
小学生学习指导(低年级)(2021年6期)2021-07-19 06:06:56
小学生学习指导(高年级)(2021年6期)2021-06-19 05:37:32
数学小灵通·3-4年级(2020年12期)2021-01-14 00:58:44
小学生学习指导(中年级)(2020年12期)2021-01-08 02:50:08
数学小灵通·3-4年级(2017年12期)2018-01-23 03:38:05
读写算·高年级(2016年3期)2016-05-30 01:53:46

