运用“四度六步”教学法提升乡村初中数学教学实效

韦献平

【摘 要】  “四度六步”教学法的主要内涵就是清晰掌握课程标准、教材内容、学生学情，根据“温故、引新、探究、变式、尝试、提升”等六个环节，巧妙设计教学方案，从而实现教学目标，努力追寻具有一定温度、梯度、宽度、深度的课堂，让师生能共同绽放异彩.本文讨论如何应用“四度六步”教学法提升乡村初中数学教学实效.

【关键词】  初中数学；“四度六步”；课堂教学

根据我国所颁布的《我国义务教育质量检测》相关内容得知，和小学生相比，初中学生的学业水平、数学兴趣、学习自信心等明显下降.而学生的数学学习焦虑程度却明显提升.而且，我国的教育领域正在面临全面改革，身处这一阶段的乡村初中数学教师应努力思考、不断创新，巧用“四度六步”教学法，提高学生的数学知识学习兴趣，帮助学生获得成功感，构建精彩的初中数学课堂.

1 “四度”课堂教学主张

1.1 追求有温度的课堂

长久以来，乡村的初中数学课堂让诸多师生都有一种“冷”的感觉，很多学生认为数学知识难学，数学课程无趣  [1] .在实际授课期间，多数都是教师热情地讲解知识，学生很少与教师互动，导致课堂温度下降到“零”.而有温度的课堂是平等的、民主的、和谐的，师生、生生会进行温情的互动，每个学生都能收获颇丰，受到良好的激励与鼓舞.这样的课堂能让师生充满动力，在提升学生学习质量的同时，促进师生共同进步、提升.

1.2 追求有梯度的课堂

梯度课堂主要指的是，教师根据学生的不同层次，帮助班级整体学生获取提升  [2] .分层教学的本质含义就是由教师根据学生现阶段的能力、水平、潜力等情况，合理地把学生分成水平相近的小组，采用合理的授课手段，促进学生的整体进步与提升.同时，通过追问激发学生思维，培养学生的主体意识，促使学生主动参与课堂.而追问需要保证质量，避免过于形式，重点追求实效.其次，教师应掌握好提问时机，并给予学生正确引导，关注问题的梯度，强化学生体验.

1.3 追求有深度的课堂

深度课堂主要指的是，教师针对教材、课程标准等进行深度钻研，借助有效手段努力体现出知识的本质，师生的深刻思考使教学更加轻松、简单、生动.授课期间，教师应积极指导学生深度感知数学知识的本质，以及其中蕴含的思想、方法，助力学生数学核心素养的生成.同时，教师要为学生设计一定的挑战性学习主题，使学生更加集中投入.如“一题多解”“一题多变”等，培养学生的创新思维能力.

1.4 追求有宽度的课堂

追求有宽度的课堂主要指的是，数学课程教学标准的规定范围、学生能接受的知识范围、学生具有的迁移能力、不同學科间的知识融合等，指导学生通过课内知识的共同学习逐渐延展到课外的自主探究.教师应避免“灌输式”“照本宣科”的教学，而是要让知识、解题方式、教学手段、学生群体“活”起来，促使学生能做到融会贯通、学以致用.针对性地分析旧知识与新知识的关联，适当地引出新知，帮助学生学会知识迁移.同时，教师还应努力融合不同学科，帮助学生构建完整的知识结构，创设丰富的情境，全力发展学生的数学核心素养，促使学生发挥自身的数学学习潜能.

2 “六步”初中数学教学环节设计方法

2.1 “温故”环节的设计

长期的乡村初中数学实践中，学生不仅不喜欢学习数学知识，学生的整体数学成绩还呈现出了较为严重的“两级分化”现象.主要原因就是学生不具备良好的习惯，学生所积累的知识量差异较大，且学生之间的目标完成情况也有所差异.因此，教师应利用有效手段减少学生间的差异  [3] .

教师在设计“温故”环节时，应掌握以下要领：（1）“温故”应重点指向学生之前课程中学习的数学知识；（2）“温故”应与本次课程的新知识相关；（3）“温故”的设计要结合旧知识，为新的知识做铺垫.

例如   以“有理数的加减乘除混合运算”教学为例，从以下两个二问题进行“温故”：

（1）我们目前都学习了哪些运算？

（2）你能说说小学时加减乘除混合运算的顺序是怎样的吗？

通过这样设计和复习旧知识，为本节课进一步学习有理数的加减乘除混合运算做准备.

2.2 “引新”环节的设计

在引入环节创设情境可以激发学生的学习兴趣.因此，教师应重视情境创设，全面引出新知识.

教师在具体设计“引新”环节时，首先应立足学生现有的知识储备和经验，创设一种符合学生需求的情境，并保证情境能促进新知、旧知的联系；其次，教学情境应体现出教学主题、核心内容，让教学更加自然地过渡到新知识；最后，“引新”这一环节应具有一定的开放性、探究性，将知识融于情境，激活学生兴趣，满足学生需求.

例如   以“二次函数”的引入为例.

雨后天空的彩虹，公园里的喷泉，跳绳等都会形成优美的曲线（课件展示图片），这些曲线能否用函数关系式表示？

学生思考后回答，教师点拨：这是我们今天需要学习和研究的“二次函数”数学模型.

以学生熟悉的问题导入，不仅能引起学生的兴趣，还能引导学生思考，引出新课题.

2.3 “探究”环节的设计

自主探究是新课标倡导的学习方式，需要学生通过教师的引导，自主探究知识、总结知识、形成观点等  [4] .教师设计“探究”环节时，应设计好教学问题，保证问题的趣味性、启发性、引导性，以此激活学生思维、兴趣、经验.另外，教师还要保证探究的深度、广度，创办不同类型的教学活动，鼓励学生主动参与其中，组建合理的学习小组，让学生感受合作学习的价值和意义，进而在共同探究中成长.

例如   以“平行四边形对角线性质”的探究为例.

首先创设情境：如图1所示，在平行四边形ABCD中，连接对角线AC、BD，使AC、BD相交于点O.

教师提出问题：

问题1    猜猜看线段OA和OC、OB和OD长度有什么关系？

学生自主猜想可能得到：AO=CO，BO=DO.

教师引导学生用文字语言描述自己的发现，教师板书.

板书（猜想：平行四边形对角线互相平分.）

问题2   量一量：拿出手中的平行四边形纸片，测量出四条线段的长度，验证你的猜想是否正确.

此过程让小组合作测量后，反馈测量结果，引导学生观察数据，发现其中的规律：

OA=OC，OB=OD.

接着教师用几何画板演示验证：

OA=OC，OB=OD.

问题3   证一证：我们在画图和测量的过程中都存在误差，因此我们的猜想需要做推理证明，你能证明这个推测吗？

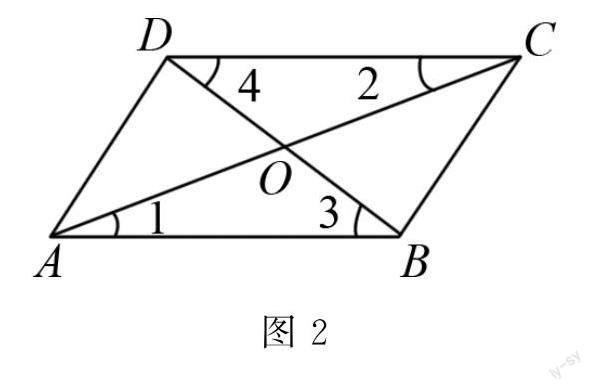
如图2，平行四边形ABCD的对角线AC、BD相交于点O.

求证：OA=OC，OB=OD.

同时，要求学生思考是否还有其他解法.各小组尝试用不同的方法进行证明并展示成果，进而归纳出平行四边形的对角线的性质.当然此过程教师可以适时引导点拨.

整个探究过程，以学生为主体，教师设计的问题为学生提供了思考导向，既能满足素质课堂的需求，让学生自由地进行探究，又能确保教学的有效性和目标  [5] .

2.4 “变式”环节的设计

教师在设计“变式”这一环节时应适当的应用“一题多解”“一题多变”等方式指导学生练习，鼓励学生勇敢地提出问题，主动交流、沟通，相互展示、分享，逐渐将练习引向深处，让学生能力达到新层次.

例如   在进行“用待定系数法求二次函数解析式”教学时，教师可以设计如下的变式题：

根据下列条件，选取你认为合适的方法求出对应二次函数的解析式：

（1）已知二次函数的图象经过点（0，2），（1，1），（3，5）；

（2）已知抛物线与x轴交于点（-1，0），（2，0），且经过点（1，2）；

（3）已知二次函数y＝ax  2 +bx+c，当x =3时，函数取最大值10，且它的图象在x轴上截得的线段长为4.

通过一题多变，让学生在碰到不同条件时能灵活运用一般式、顶点式或交点式来解答.这样不仅可以拓宽和扩展学生解决问题的思维，还可以激发学生对数学学习的兴趣，提升数学核心素养.

2.5 “尝试”环节的设计

“嘗试”环节的设计中，教师应满足学生的认知特点，遵循“由简到难、由浅到深”的原则，构建“高而可攀”的数学问题，让学生能轻松地解决，从而提升教学效果.

例如   “二次函数”的“尝试”环节可做如下设计.

写出以下各函数的关系式，判断它们是什么类型的函数.

（1）一个直角三角形的两条直角边长分别是为x、2x，写出其面积y与x的关系式.

（2）长方形绿地的长为20米，宽为15米，如果将其长、宽各增加x米，写出扩充后长方形绿地的面积y和x的关系式.

（3）某超市在周年庆时，原来某种品牌的苹果每千克为20元，准备进行两次降价，如果每次降价的百分率都为x，经过两次降价后的价格为y（元），试求出y与x之间的函数关系式.

这样的尝试练习设计从简单的问题情境开始，考查学生如何根据实际问题列出二次函数关系式.从多个角度进行考察，让学生获得对二次函数深层次的理解，达到学有所成的目的.

2.6 “提升”环节的设计

教师设计“提升”环节时，应掌握以下要领：一、帮助学生走出思维困境，适当地给予学生点拨和引导；二、为学生提供思考、学习的正确方向，合理地总结、归纳关键知识信息；三、激活学生兴趣，保证课堂实效，提升学生综合能力.

例如   “二元一次方程组”的“提升”环节可做如下设计.

2.6.1 归纳总结

互动环节   请学生按照分组，自己归纳总结本课知识点，形式不限，然后交流分享展示.

2.6.2 迁移提升

（1）《武大郎卖饼》是一个很有趣味的古代诗词：武大郎卖饼串满街，甜咸烧饼销得快，甜三咸二两厘一，咸四甜二两厘二；各买一只甜咸饼，武大饼价该咋卖？聪明的同学你能计算出甜咸饼的价格吗？（只列方程组）

（2）小明到邮局寄包裹，用了6.4元的邮资，2元和0.8元两种邮票共贴了5张，你能算出这两种邮票各有多少张（只列方程组）吗？

这样设计“提升”环节可以让学生整理自己学到的知识，形成知识体系，养成良好的学习习惯，提高学生的学习能力.

3 结语

综上所述，乡村初中教师在应用“四度六步”教学法提升数学教学实效的过程中，需要掌握其中的内在逻辑，最关键的就是关注学生主体，落实以生为本，促进自身与学生的共同发展，最终构建出精彩的初中数学课堂.

参考文献：

[1] 焦燕.“双减”背景下初中数学课堂教学实效提升新举措[J].教书育人，2022（04）：20-21.

[2]罗同.聚焦课堂提问技巧，提升初中数学教学实效[J].学苑教育，2021（32）：31-32.

[3]王倩.浅析新课程理念下提高初中数学课堂教学实效的策略[J].天天爱科学（教学研究），2020（03）：66.

[4]高泽荣.“双减”背景下初中数学课堂教学实效提升新举措[J].亚太教育，2022（19）：125-127.

[5]周华娟.开放性教学，构建实效初中数学课堂[J].数学大世界（上旬），2021（02）：57.