模型化视角下的中考试题研究——一类直线旋转问题的解决策略

龚 辉 (江苏省太仓市高新区中学 215413)

图形变换问题是初中数学学习的重点和难点,也是中考试卷上的高频考点,不仅在平面几何背景下呈现,在函数背景下也经常出现．在对众多的相关题型进行研究时我们发现,很多题目以不同问题背景、方式呈现,但其核心方法大多相似,这就要求我们用数学建模的思想,对同类问题的性质和本质理解透彻,抓住问题的关键特征,探究图形变换的基本题型,做到以不变应万变．

《义务教育数学课程标准(2022年版)》指出,数学核心素养之一为“会用数学的语言表达现实世界”,具体表现为模型观念和应用意识[1]．模型观念就是用数学符号、公式、程序、图形等工具、手段对实际问题或某一类相似问题的本质属性进行抽象而简洁的刻画,来解释某些客观现象,或找出化解实际问题的最优策略[2]．

然而,目前有些课堂教学忽视了学生数学建模思想的培养,知识的讲解零敲碎打、例题的讲解就题论题,制约了学生数学归纳能力和应用能力的提升．

本文从直线绕一点旋转这一较小的切口入手,以建模的思想探究、提炼、挖掘这一类问题的核心方法,形成这一类问题的模型化解决策略,也为研究其他图形变换问题提供一种思路．

1 云海百川归——问题源起于基本模型

模型问题如图1,在平面直角坐标系内,已知点A(0,2),B(1,4),作直线AB并将该直线绕点A顺时针旋转45°得直线AC,求直线AC的函数表达式．

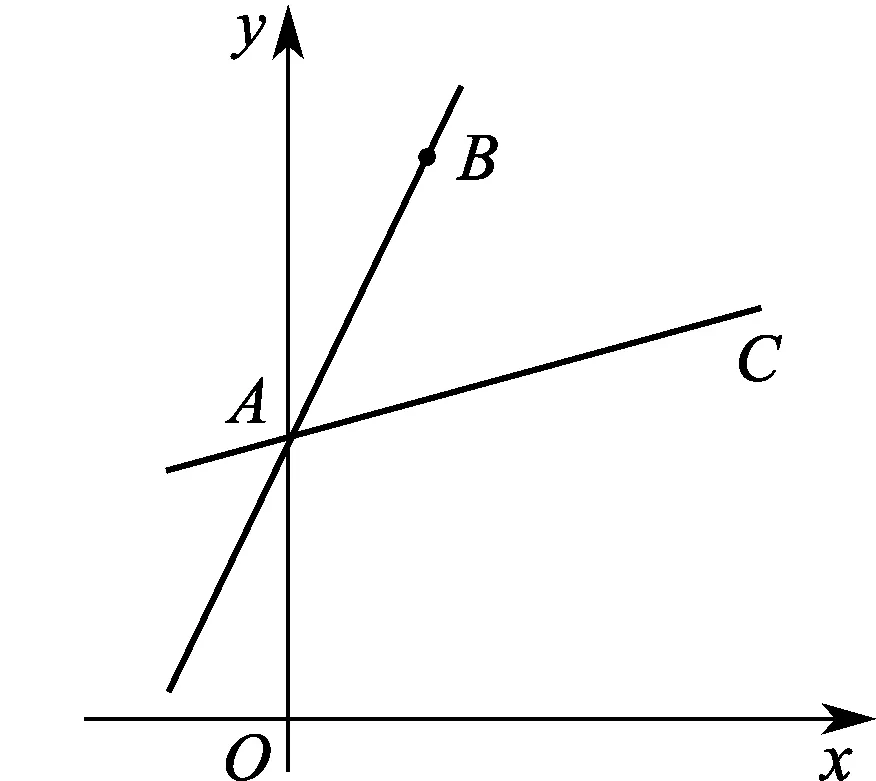
图1

分析 本题的关键是特殊角45°,它是等腰直角三角形底角的度数,因此可以通过作高构造以∠BAC为一个底角的等腰直角三角形．

在这个思路下,存在两种构图方式:一是过点B作直线AC的垂线,二是过点B作直线AB的垂线．这两种构图方法的优劣可通过下面两种解题方法的对比进行评判．

当直角坐标系中出现了直角三角形,很容易就联想到构造“一线三直角”的“K”字形基本模型,将坐标系内点的坐标与横向、纵向的线段关联起来,从而可以求出直线AC上除点A外的另一个点的坐标,则直线AC的函数表达式可求．

解法1如图2,过点B作BH⊥AC于点H,过点H作y轴的平行线,分别过点A,B作AE⊥EH于点E,BF⊥EH于点F．

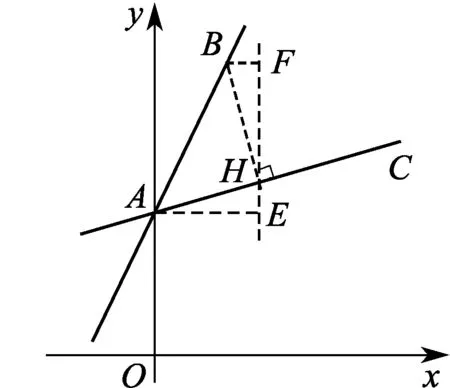
图2

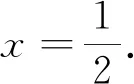
解法2如图3,过点B作BH⊥AB于点B,作BE⊥y轴于点E,作HF⊥BE于点F．

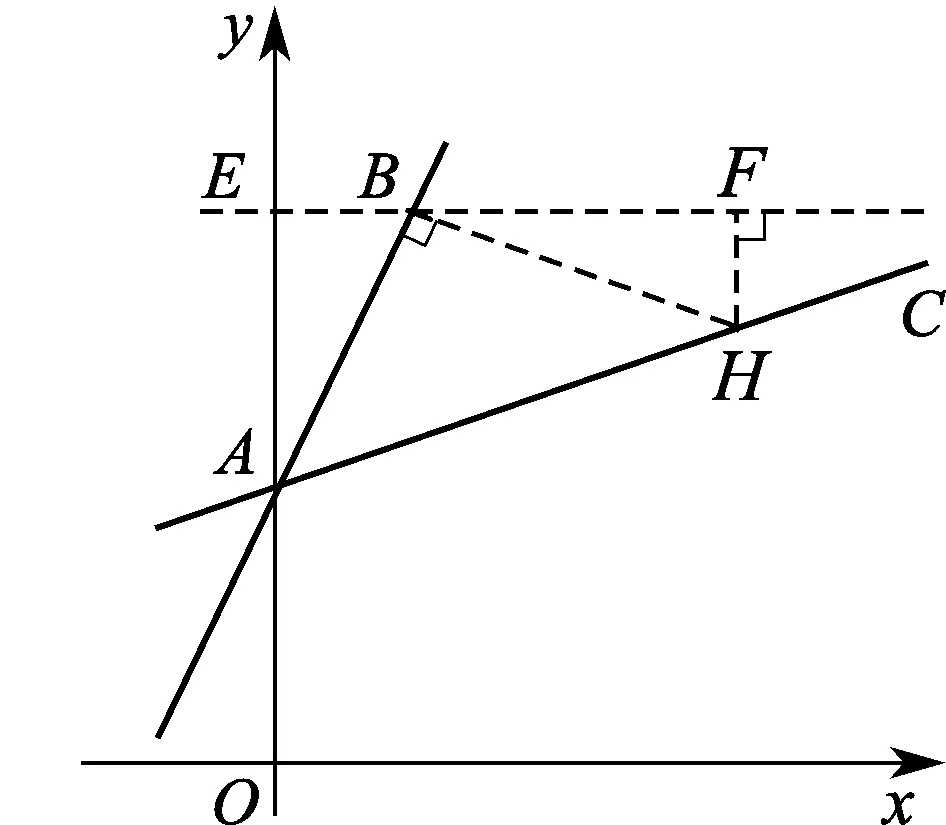
图3

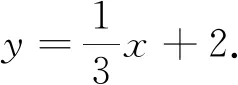
反思 本题在构造等腰直角三角形和“K”字形基本模型的框架下,如何作高构造等腰直角三角形出现了两种不同的方法．根据上述两种解法的对比,我们可以直观地感受到,以已知点(如本题中的点B)作为垂足的构造方法,可以更快地将已知坐标与线段产生关联,从而简化计算过程．

模型变式1在平面直角坐标系内,已知点A(0,2),B(1,4),作直线AB并将该直线绕点A顺时针旋转60°得直线AC,求直线AC的函数表达式．

分析 变式1将45°改为60°,基本思路不变,即构造直角三角形和“K”字形基本模型,方法如下:

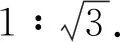
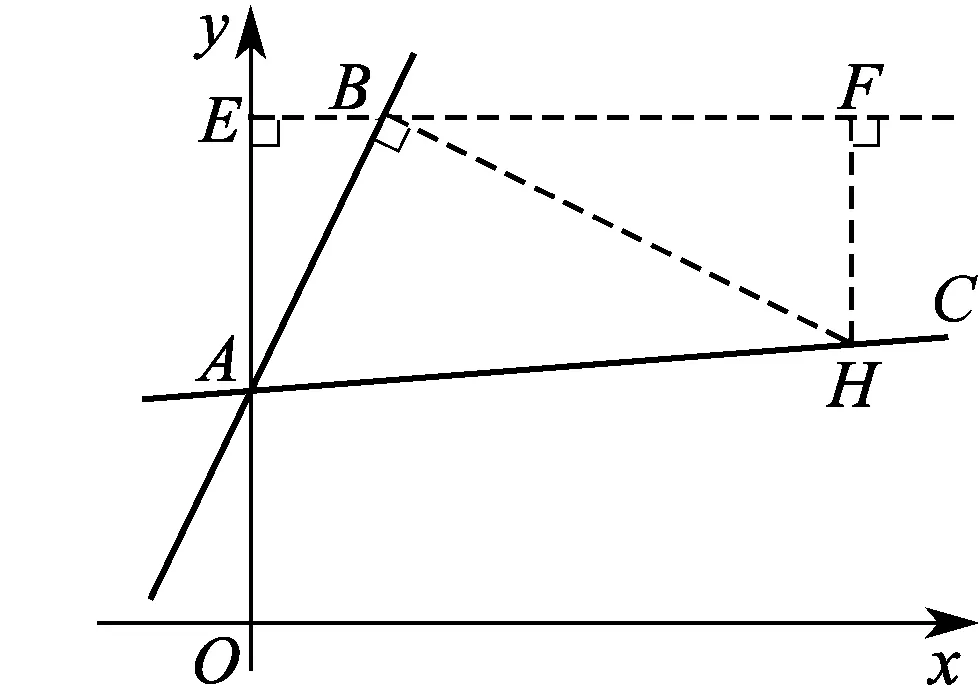
图4

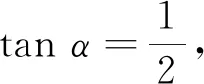
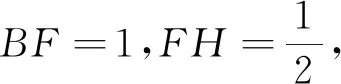
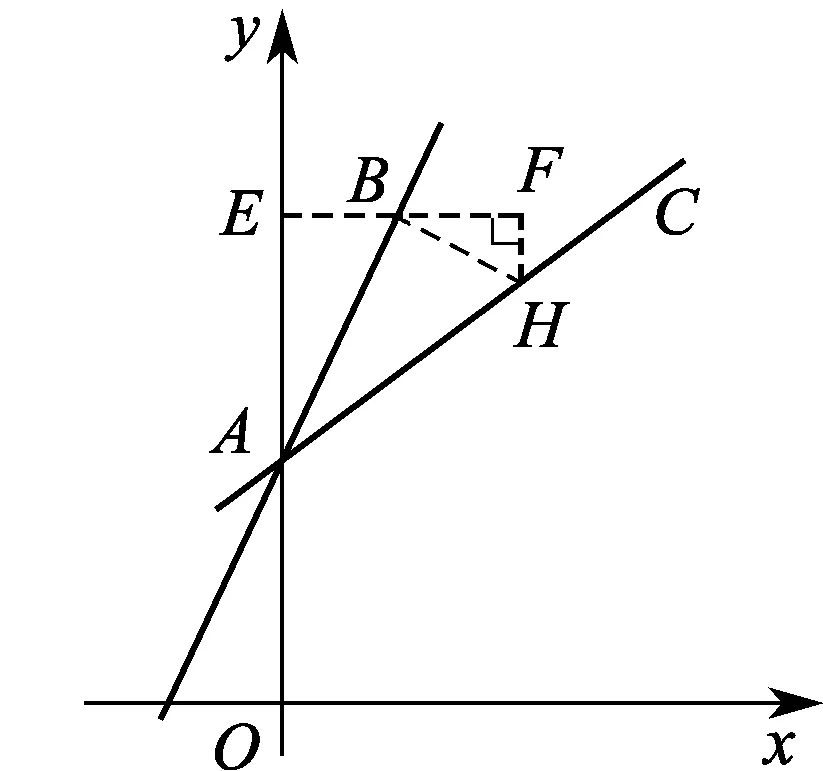
图5

2 拨得云开又见明——指向基本模型的问题解决

数学建模通过具体问题抽离出数学模型的思维过程,其根本就是要抓住数学问题的本质,在变化中寻找不变的规律,将较为困难的问题指向基本模型的解决,从而提高学生的思维品质和解决问题的能力[3]．在问题解决的过程中,经常会碰到两个难点:一是学生模型意识的建立,二是在多变的背景中抽象出数学模型,并运用模型解决问题．

2.1 多向思维,以通法理解模型

例1(2022年苏州市中考试题)如图6,点A的坐标为(0,2),点B是x轴正半轴上的一点,将线段AB绕点A按逆时针方向旋转60°得到线段AC．若点C的坐标为(m,3),则m的值为( ).

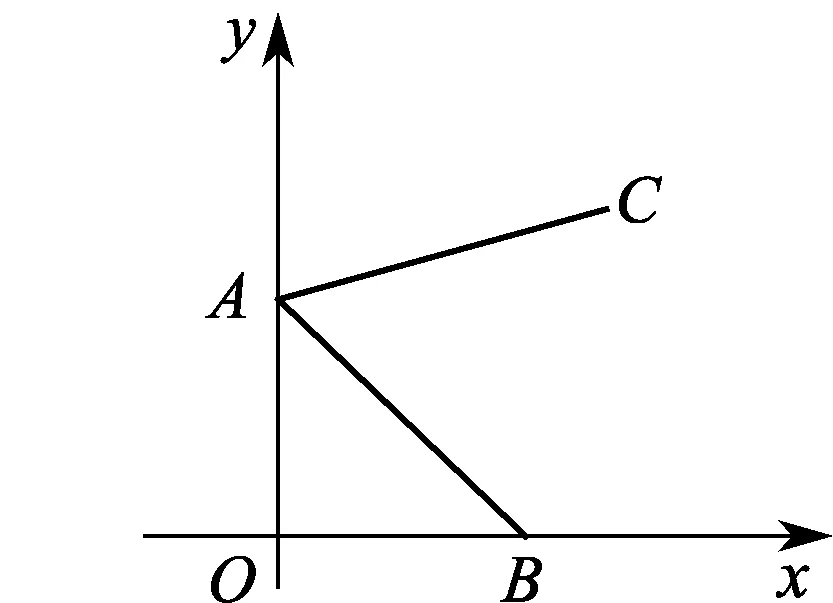
图6

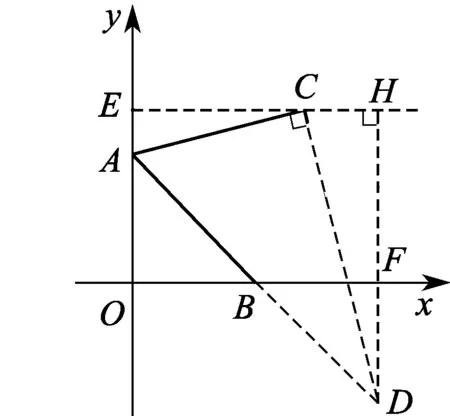
图7

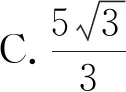
分析 本题中的AC是AB绕点A逆时针旋转60°得到的,属于直线绕定点旋转的基本模型．由于两个端点C和B均不是已知点(两个点仅已知纵坐标),因此根据基本模型的构图方法,本题有4种作高的方法:过点B作AB边上的高、过点B作AC边上的高;过点C作AB边上的高、过点C作AC边上的高．

下面以过点C作AC边上的高为例,说明基本模型在解决这一类问题时的强大功能．

过点C作CD⊥AC,交AB的延长线于点D,过点C作CE⊥y轴于点E,过点D作DH⊥EC于点H,交x轴于点F．

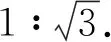
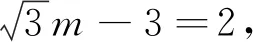
其他几种作高的方法可以类比上面的解法处理．

说明本题与模型的区别在于旋转直线上的点B或点C均不是已知点,因此不论如何作高构图,相关运算均含参,对学生的符号意识有一定的要求,并且在构造“K”字形后需要一定的推理才能得到方程．

2.2 揭示本质,以化归联想模型

有些数学问题并不是按模型的背景呈现,并且经常与函数图象结合,增加了题目的综合性和迷惑性．因此,我们在分析问题时,要保留最关键、最本质的要素,从背景图形中分离出基本模型,然后结合基本模型的处理方法,就可以较好地突破难点．

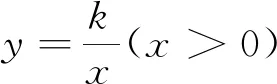
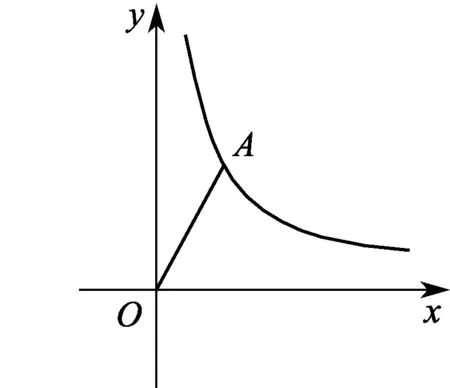
图8

分析 本题并没有以直线旋转的背景呈现,但是通过分析发现,解决本题的关键是求出OA绕点O旋转一个定角后所得直线OB的表达式,这正好是基本模型．但是题目并没有明确旋转的方向,因此本题有两种情况需要讨论．

先处理OA绕点O顺时针旋转的情况．根据上述基本模型所归纳的方法,本题应以已知点A为垂足作高并构造“K”字形.具体分析过程如下:

如图9,过点A作AC⊥OA,交直线OB于点C,AE⊥y轴于点E,过点C作FH⊥x轴,分别交AE、x轴于点F,H．

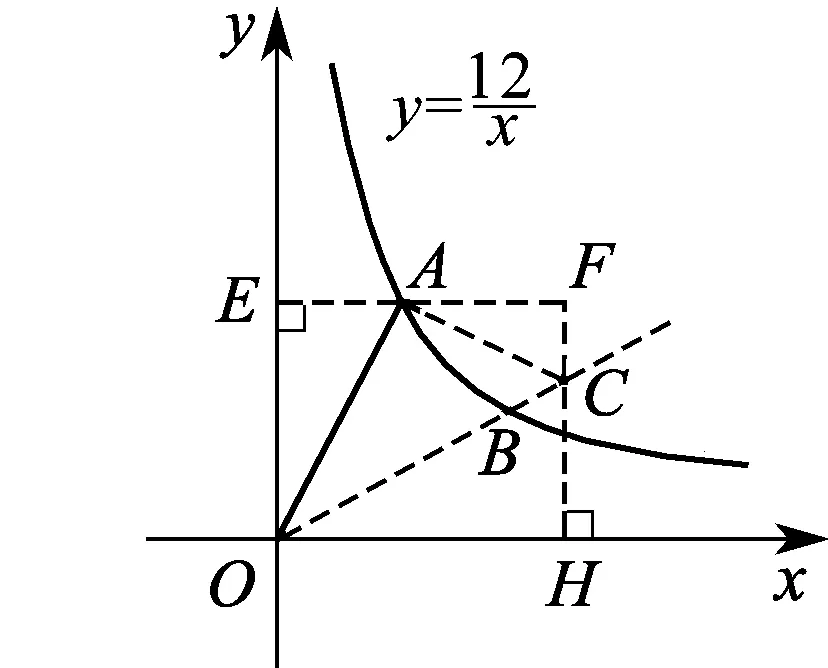
图9

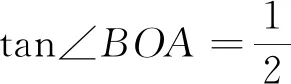
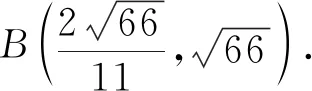
2.3 拓展思路,以构造形成模型

在几何背景下也可能会涉及上述模型,在处理这类问题时,可以运用构造的方法,建立平面直角坐标系,转化为模型问题,从而解决问题．

例3如图10,在△ABC中,CO⊥AB于点O,OA=8,OB=12,且tan∠ACB=2,求OC的长．

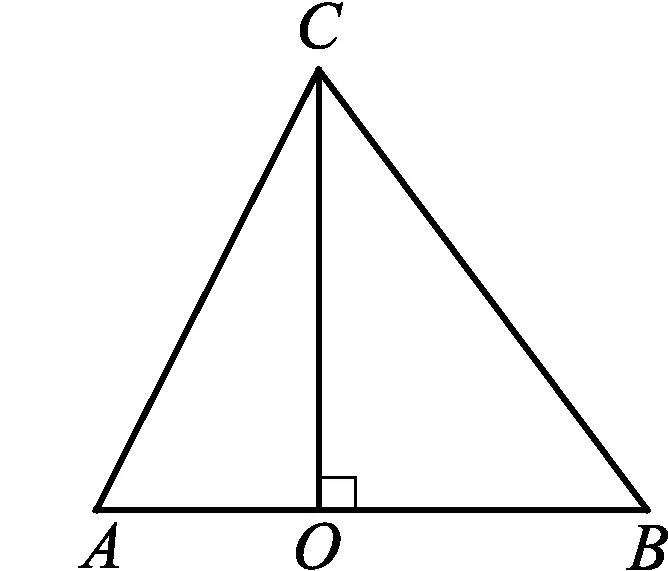
图10

分析 本题为直线CB绕点C顺时针旋转一个定角得直线CA,其本质为直线旋转的基本模型,可考虑作高构造“K”字形来解决．因为点A,B均为已知点,因此以点A或点B为垂足构造垂线的方法均可行．本题以点B为垂足,略解过程如下:

分别以AB,OC所在直线为坐标轴建立如 图11所示的平面直角坐标系．以点B为垂足作BD⊥BC,交CA的延长线于点D,过点B作BE⊥x轴,分别过点C,D作CE⊥BE于点E、DF⊥BE于点F,交y轴于点G．

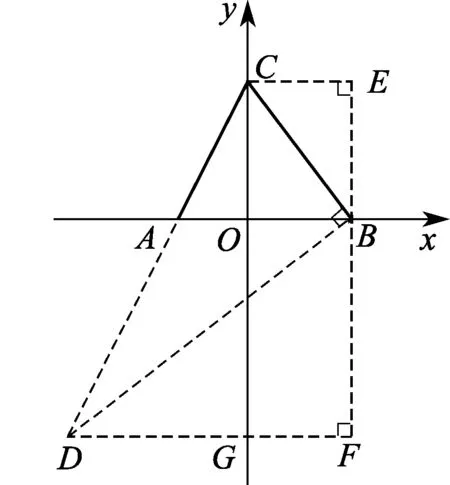
图11

易得△BCE∽△DBF,且相似比为1∶2．由CE=12可得BF=24,设OC=x,则BE=x,得DF=2x,故DG=2x-12．又由△CAO∽△CDG,可得即解得

x=16(x=-6舍去)．即OC的长为16．

以点A为垂足作AD⊥AC的解法与上述方法相仿．

总之,对数学问题核心方法的掌握,以及数学问题通性通法的研究是非常重要的．模型化思想能帮助我们更好地理解并有效地解决一类思维本质相近的数学问题,具有较强的普适性．如果我们在平时的教学中,能够适当地注意数学问题模型化方法的讲授,那么对于提高学生综合运用数学知识去分析问题、解决问题的能力必将大有裨益,对教师自身专业素养的提升也有重要作用．