设计有效题组，实现高效学习

江苏省南通市城西小学校 陈莉莉

随着课程改革的稳步推进，题组教学引起了广大教师的重视和关注。所谓“题组教学”，就是将表述相似、内容相关、思维相近的题目放在一起，形成组合，帮助学生厘清知识的易错点、混淆点。小学阶段的学生，年龄尚小，学习能力不强，思维能力也不发达，在课堂中难以透彻地掌握所学知识。同时，很多教师设计的习题枯燥、单一，导致学生的参与性不强，容易受到知识表面现象的蒙骗，形成思维障碍，甚至出现错误，并没有发挥出作业应有的功效。因此，作为新时代的数学教师，应顺应学生的学习需求，沟通知识点之间的联系，为学生设计有启发性、层次性、开放性的题组，更好地提升学生的辨析力、判断力和创造力，使学生享受数学学习的精彩和魅力。

一、设计相似性题组，促进学生探索

（一）运用相似性题组，深化学生认知

学习数学知识的过程，也是逐步走向深入的过程。在教学中，教师经常发现，学生在学习后续知识时，容易受前面知识的干扰，形成负迁移，甚至会出现错误。针对此种情况，教师可以为学生设计相似性题组，激活学生已有的知识积累，沟通知识点之间的联系，升华学生的认知，增强学生对所学知识的印象，从而构建起新的知识结构。教学实践证明，这样的训练形式，有助于开发学生的智力，使他们对知识的认知产生“质”的飞跃。

分数应用题是小学数学课本中的重要内容，也是学生学习的“拦路虎”，尤其学生在“数量”和“分率”的区分上经常出现问题。针对此种情况，教师为学生设计了这样的题组：①工地上有一段方钢，长米，用去米，还剩下多少米？②工地上有一段方钢，长米，用去还剩下多少米？

显然，题组中的两道题目只相差一个字，但解题的方法却发生了根本性的改变。两道题目中方钢的总长度是相等的，只是用去的部分不同，一段是“用去米”，一段是“用去”。第①题中的表示的是具体的数量，根据“原来的长度-用去的长度=还剩下的长度”，列出算式，就可以算出最终的结果。第②题中的表示分率，方钢原来的总长度是单位“1”，应先计算出单位“1”的是多少米，然后再用“方钢原来的长度-用去的长度=还剩下的长度”，列出的算式为可见，这样的题组训练，可以促进学生对“分率”与“数量”的辨析，提升学生分数、百分数应用题解题的正确率。

（二）运用相似性题组，实现规律探索

探索规律是数学新课标提出的重要内容之一，属于“数与代数”领域。这部分内容的教学，主要是让学生经历从特殊到一般、从具体到抽象的归纳过程。显然，找规律的教学，关注的重点不在于规律本身，而在于“找”的过程，要让学生经历有意义的探究过程，学会用数学的眼光发现规律。可见，为学生搭建思维“脚手架”显得非常重要，而相似性题组的应用，便是有效的途径之一。因此，教师应针对规律的内容，将其融入题组训练中，让学生自主探索，直击规律的本质内容。

在教学“减法的运算性质”时，教师联系教学内容，为学生设计了相似性题组：

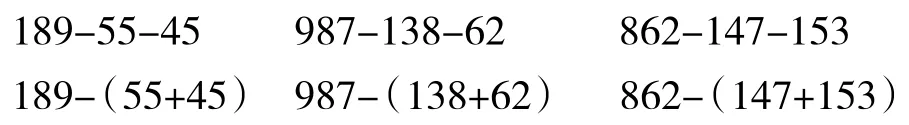
教师先出示最左边的两道算式，让学生按照本来的运算顺序进行计算。学生发现，两道算式的结果都是89，55和45可以凑成整百，计算时容易一些。此时，教师并没有急于让学生猜想规律，因为学生的思维还处于困惑中，而是出示了后面的四道算式，让学生计算。在此过程中，学生发现后面两组算式上下两道算式的结果也是相等的，于是作出了大胆的猜想：一个数连续减去两个数，就等于这个数减去两个数的和。教师让学生继续举例进行验证，看自己的发现是否正确，并思考自己的发现如何用字母表示出来。学生发现猜想是正确的，并用a-b-c=a-（b+c）表示自己的发现，从而架构起减法运算性质的算式模型。

二、设计对比性题组，实现知识整合

（一）运用对比性题组，提升辨析能力

对比是一种非常重要的数学思想，也是获取知识的有效方式。学生在解答与所学内容相关的题目时，往往不注重对题目中的条件和结构进行辨析，仅凭借印象进行解答，导致错误时有发生。因此，面对这样的情况，教师可以将学生易错的知识点编排成对比性题组，让学生在对比的过程中，厘清解题思路，避免走入思维定式的尴尬境地，取得“1+1>2”的教学效果。

在教学“百分数”的知识时，教师为学生设计了对比性题组，让学生学会对题目中的条件进行审视。①某林场购进一批树苗，共2500棵，其中，松树苗占60%，剩下的是柏树苗。松树苗比柏树苗多百分之几？②某林场购进一批树苗，共2500棵，其中，松树苗占60%，剩下的是柏树苗。柏树苗比松树苗少百分之几？

可见，解答这两道题目时，都是先求出树苗相差的棵数，作为被除数，但单位“1”不同，决定了除数不同。第①题中单位“1”是“柏树苗的棵数”，第②题中单位“1”是“松树苗的棵数”，在解答的过程中，区分谁是“被比较量”显得尤为重要。这样的题组训练，可以提升学生的数学辨析力，促进学生思维的发展。

（二）运用对比性题组，形成结构认知

数学新课标提出了很多新颖的教学理念，而结构化教学便是其中重要的一种。结构化教学倡导让学生在数学课堂中经历结构化的学习，旨在让学生掌握结构化的知识，在头脑中形成结构化的思维，发展数学素养。但在以往的教学中，教师往往采用的是“一课一教”的教学模式，即一堂课完成一个例题的教学，然后围绕例题设计相关的练习，让学生进行重复性训练，达到巩固所学知识的目的。显然，这样的做法不利于学生结构化思维的形成。在教学中，教师应引导学生对所学知识进行横向和纵向的联系，促进学生结构化认知体系的形成和发展。

在教学“长方形和正方形的面积”后，教师发现，很多学生对周长和面积并没有清晰的理解，甚至会错误地认为面积相等的长方形，周长也一定相等。对此，教师设计了对比性题组：①准备24个边长为1厘米的正方形纸片，拼成长方形，求所拼长方形的周长是多少？面积是多少？②用24根1厘米长的木棍围成长方形，求围成的长方形面积是多少？周长是多少？

上述对比性题组的引入，可以让学生在解答的过程中发现：周长相等，面积不一定相等；面积相等，周长也不一定相等。这样的学习过程，充满了理性的思辨，实现了思维结构的突破。

三、设计拓展性题组，提升思维能力

（一）运用拓展性题组，进行变式训练

数学课堂的教学任务，除了要让学生收获数学知识，还要培养他们缜密的数学思维。在教学中，教师时常发现，很多学生对课堂中教师所讲解的例题掌握得很好，但只要变换问题中的条件，学生的答题效果就不尽如人意。究其原因，学生习惯于顺向思维，而变式问题改变了原先的条件和问题，需要逆向思维解答时，学生往往理不清头绪。因此，在平时的教学中，教师应注重学生这方面的训练，而拓展性题组的运用，就可以帮助教师达到这样的目的。

在教学“梯形的面积”时，教师为学生设计了这样的拓展性题组：①一块梯形花圃，上底是100米，下底是150米，高是120米，求它的面积是多少平方米？②一块梯形花圃，上底是100米，下底是150米，面积是15000平方米，求它的高是多少米？

题组中的第①题，难度很小。学生只需要将相关数据代入梯形的面积计算公式，就可以计算出最终的结果，也可以根据三角形的面积计算公式直接进行解答，把相关的数据代入公式即可。此题旨在强化学生对所学知识的印象，让学生把基本方法学懂、学会。第②题需要学生运用逆向思维进行解答，因为是求高，而不再是求面积。在此过程中，很多学生会直接用“15000÷（100+150）”，从而出现错误。教师应让学生明确，首先要将“梯形的面积乘2，再除以其上底、下底的和”。这样的训练，既可以开发学生的智力，又可以培养他们的逆向思维能力。

（二）运用拓展性题组，培养发散思维

数学新课标指出，在教学时，教师要引发学生的数学思考，鼓励学生的创造性思维。可见，培养学生的创造性思维是数学课堂的重要任务之一，也是发展学生核心素养的重要途径。教师应将其落到实处，而拓展性题组的应用便是有效的渠道之一。教师应针对相关内容，为学生设计开放程度高、灵活性强的题组，让学生探求解题途径、发散思维、享受创造的快乐。

在教学“长方体和正方体的表面积”后，教师针对学情，设计了拓展性题组：①一块长方体木块，长1.2米，宽0.8米，高1米。将它锯成两个长方体，表面积可能会增加多少？②一块长方体木块，长1.2米，宽0.8米，高1米。从中挖去棱长0.5米的正方体，剩下木块的表面积是多少？

可见，这两道题目具有很强的开放性。第①题中并没有强调锯的方向，锯的方向不同，增加的表面积也会有所变化。第②题中并没有限定挖去正方体的位置，位置不同，剩下木块的表面积也会有所区别。这样的题组训练，既可以培养学生的空间观念，又可以提升学生思维的缜密性和创造性，可谓一举多得。

综上所述，题组教学是切实可行的教学方式之一，题组的有效运用，可以帮助学生辨析知识，将零碎的知识串联起来，强化学生的数学素养，满足他们后续学习和发展的需求。在以后的教学中，教师应从培养“全面发展的人”这个要求出发，有意识地进行知识重组，让学生在题组训练中系统地掌握所学知识，提升思维品质，形成数学关键能力，将课堂教学效益最大化！