明题意 理关系 建模型

屈婷

《用百分数解决问题》是人教版数学六年级上册第六单元《百分数（一）》例5的内容，旨在让学生用百分数解决“两次增减变化”问题，培养学生的探究意识，提高学生解决问题的能力。

一、数形结合，夯实审题基础

提取题目中的有效信息、明晰数据所表达的意思，才能看到问题背后的数学本质。教师可以引导学生用图示表征题意的过程，促进学生理解问题。

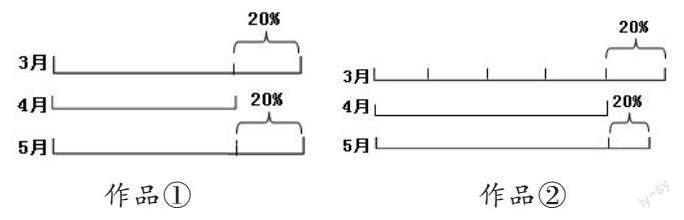
课始，笔者创设以下问题情境：“某商品4月的价格比3月降了20%，5月的价格比4月涨了20%。张阿姨和李阿姨分别在3月和5月购买了该商品。谁买得便宜？”学生猜想结论后，笔者让学生画图表征题目信息，并收集了两件有代表性的学生作品（如下图）。

学生认为两件作品都表示出商品3月、4月、5月的价格，降的20%和涨的20%也表示得很清楚。笔者引导：为什么要先画商品3月的价格？学生回答：因为3月的价格是标准，画线段图时要先画标准量，再画比较量。接着，笔者让学生分析两幅作品有什么不同。学生发现作品①没有关注“降20%”和“涨20%”的线段长度，而作品②将表示3月价格的线段平均分成5份，其中1份与表示“降20%”的线段一样长。然后，笔者引导学生讨论“降20%”是谁与谁比、这部分线段是不是随便画多长都可以，并让学生思考哪幅作品能更准确地表示商品4月的价格比3月降低20%。学生讨论后明确：“降20%”表示“4月与3月相比，商品价格少了，少的数量是3月商品价格的20%”，用分数表示是五分之一，这部分线段的长短不能随意画，作品②的画法更准确。最后，笔者引导学生思考表示“涨20%”与“降20%”的线段长度是否一致，怎样确定“涨20%”的线段画多长。通过交流，学生发现：“涨20%”表示“5月与4月相比，商品的价格涨了，涨的数量是4月商品价格的20%”，画图时需要把表示4月价格的线段平均分成5段，其中一段的长度就是“涨20%”对应的长度；由于比较的标准不一样，“降20%”与“涨20%”的线段长度是不同的。

二、理顺关系，强化思路分析

本课要解决的是多步复合应用题，学生既要以两次增减的百分数的意义作支撑来建立数量关系，又要借助假设法辅助思考。教师要关注学生解决问题的思维路径，帮助学生理顺信息之间的逻辑关联，理清数量关系。

课堂上，笔者先引导学生解决列算式解决问题时会遇到的具体价格不明的问题。对此，学生提出借鉴解决工程问题的做法，假设一个价格。笔者追问：要假设商品几月的价格？假设成多少合适？学生提出要假设3月的价格，可以假设成50元、100元、1000元等方便计算的数。笔者让学生列算式解决问题，而后呈现以下两种方法：

①50×（1-20%）=40（元）  40×（1+20%）=48（元）

②50-50×20%=40（元）  40+40×20%=48（元）

笔者提问：方法①和方法②有什么相同点和不同点？学生回答：两种方法都是把商品3月的价格假设成50元，分别算出4月和5月的价格；不同的是方法①先算4月价格占3月价格的百分率，方法②先算4月比3月降低的具体钱数。笔者追问：为什么都要先算出4月的价格？学生回答：5月的价格是以4月的价格为标准变化的，只有先求出4月的价格，才能求出5月的价格。

接着，笔者呈现方法③：100×（1-20%）=80（元），80×（1+20%）=96（元）。笔者问学生方法③与前两种方法比有什么不同，它可以跟哪种方法归为一类。学生认为方法③和方法①是同一类，都是先算商品4月的价格是3月的百分之几，只是假设的3月价格不同。

然后，笔者呈现方法④：1×（1-20%）=0.8，0.8×（1+20%）=0.96。笔者设疑：这种方法与前面的方法相同吗？学生认为方法④与方法①、方法③相同，只是没写单位名称，并提出前面的方法假设的是具体价格，方法④中的“1”表示商品3月的价格对应的分率，直接算分率不用写单位名称。笔者肯定了学生的想法，并进一步引导：小刚用“1”表示商品3月的价格，列出算式“1-20%+20%=1”，有道理吗？学生回答：线段图中涨的20%和降的20%不一样长，不能直接加或减。笔者引导学生结合线段图思考：如果用“1”表示商品3月的价格，商品4月的价格怎样表示？学生讨论后认为，用“1×（1-20%）”和“1-20%”表示都对。笔者继续引导：商品5月的价格由几部分组成？加的20%是“1”的20%吗？学生恍然大悟：加的应该是商品4月价格的20%，而“（1-20%）×20%”等于16%，所以应该用“1-20%+16%”计算。

最后，笔者引导学生算出5月与3月相比的降价幅度，并提问：为什么假设的数据不同，结果却相同？学生发现降价幅度是一个百分率，降价钱数与假设钱数的关系是不变的，所以结果相同。

以上教学，学生体会到不论用哪种方法解题，都要先算商品4月的价格，它是“涨20%”的标准，这个隐藏较深的单位“1”是正确解题的关键。

三、题组对比，助力模型建构

教師构建变式题组，引导学生对比理解同类题目的数学本质，掌握这类问题的基本结构，有利于学生明确解决复杂百分数问题的一般方法与策略。

笔者先呈现第一组题，让学生独立解答。

（1）某商品4月的价格比3月降了10%，5月的价格比4月涨了10%。5月的价格和3月相比，是涨了还是降了？

（2）某商品4月的价格比3月涨了10%，5月的价格比4月降了10%。5月的价格和3月相比，是涨了还是降了？

学生列式计算，发现两道题的结果相同。笔者引导学生观察算式，思考“先降再涨”和“先涨再降”结果相同的原因。学生发现两道题都有乘（1-10%）和（1+10%），只不过先后顺序不同。笔者引导学生把分步算式改写成综合算式，从新的角度观察。学生改写后发现：两个综合算式中，只是带括号算式的位置不同，只要降和涨的百分率一样，不论是先降再涨还是先涨再降，5月的价格都比3月的价格低，因为降10%的单位“1”的量比涨10%的单位“1”的量大。

然后，笔者呈现第二组题，引导学生猜一猜哪些题目的结果可能相同。

（1）某商品的价格是a元，4月的价格比3月涨了25%，5月的价格比4月降了20%。5月的价格和3月相比，是涨了还是降了？

（2）某商品的价格是a元，4月的价格比3月降了25%，5月的价格比4月涨了20%。5月的价格和3月相比，是涨了还是降了？

（3）某商品的价格是a元，4月的价格比3月降了20%，5月的价格比4月涨了25%。5月的价格和3月相比，是涨了还是降了？

有的学生认为3道题中降的百分率与涨的百分率不同，结果未必相同；有的学生认为第（1）题和第（3）题都是“涨25%”“降20%”，只是顺序发生了变化，结果可能相同。笔者引导学生验证猜想，助推学生根据数量关系写出含有未知数（字母a）的式子。经过探究，学生发现：第（1）题和第（3）题与第一组题的规律相同，算得的结果都是a；第（2）题的算式“a×（1-25%）×（1+20%）”所得结果是0.9a，与涨和降的百分率相同的情况相比，涨的百分率少，降的百分率多，5月的价格会更低。通过对比分析，学生逐步理解了多种假设法的合理性及其内在一致性。

（作者单位：宜城市窑湾小学）

责任编辑  刘佳