从关注数学的内容到关注数学的本质
——对“‘三角形的内角和’教学设计(二)”的研磨过程
哈尔滨市经纬小学
“玉不琢,不成器。”同样,课不磨,不精彩。一节好课不是模仿出来的,不是演出来的,而是一步一个脚印研磨出来的。这节课在哈尔滨市道里区进修学校小学部马金国主任和童星老师的指导下经历了多次研讨、备课、试讲,其间经历了从关注一个知识点到关注整体架构、从关注本课设计到关注大单元备课、从关注数学内容到关注数学本质与思考的过程。
一、对教学内容的琢磨
“三角形的内角和”属于“图形的认识与测量”主题,是人教版四年级下册第五单元内容。四年级上学期学生已经会用量角器量角,在这一单元里还认识了三角形,知道了三角形的分类,本课是让学生理解和探索“三角形内角和是180°”这个重要性质,数学的核心思想是分类和转化思想。《义务教育数学课程标准(2022 年版)》在本课教学提示中指出“可以从特殊三角形入手,通过直观操作,引导学生归纳出三角形的内角和,增强几何直观”。
二、对教学设计的琢磨
基于以上分析,我最初设计了一定的情境,锐角三角形、直角三角形、钝角三角形各自拿出一个角比大小,谁会赢? 学生提议公平起见各自把三个内角合起来比大小,顺势揭示概念。 由比大小引发学生进行小组合作探究活动:动手量一量、算一算。 接着借助手中形状大小不同的三角形,采用剪、撕、折等多种方法动手把三角形的三个内角拼成一个平角,验证三角形内角和是180°。
接着让学生根据长方形的内角和是360°,把长方形分成两个相同的直角三角形,推理、验证得出直角三角形内角和是180°。
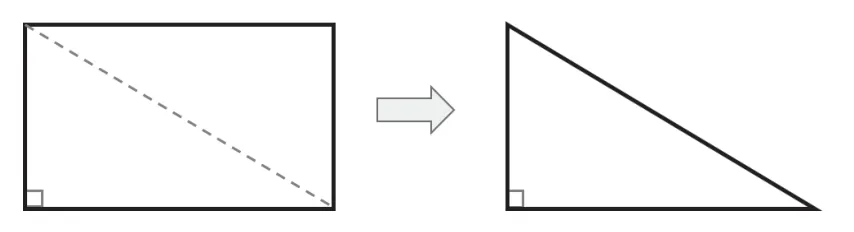
在此基础上,任意一个三角形沿着它的高都可以将它分成两个直角三角形。 两个直角三角形内角的和:180°+180°=360°,一个三角形内角和:360°-90°-90°=180°。最后是应用三角形的内角和知识解决问题,独立完成数学书第65 页做一做和第67 页的第1.2 题。
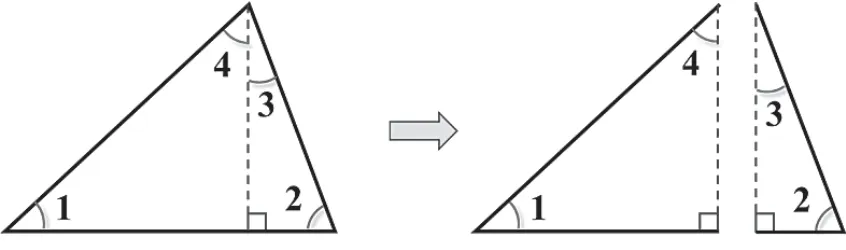
在第一次试讲过程中发现情境的创设和探究问题没有激发学生的研究兴趣,相反,四年级学生大多数知道三角形的内角和是180°,已经不是零起点。我们都说“学习要从孩子该开始、想开始的地方开始”,所以这样的教学设计没有达到使学生产生探索研究的“真需求”。 而且《义务教育数学课程标准(2022 年版)》注重教学内容的结构化,建议设计要整体分析、把握教学内容,不要局限于一节课,可以是单元整体设计,也可以跨单元、跨年级甚至跨学段进行内容模块设计,通过长期持续的教学活动,帮助学生构建支撑未来学习的数学知识体系, 把握数学学科本质,学会用整体的、联系的、发展的眼光看问题,形成科学的思维习惯。 所以我联系初中研究的三角形内角和知识,从学生已知出发,对三角形、三角形的角、三角形的内角、三角形的内角和的概念深入地逐一做出了描述性解释,使学生真正掌握三角形内角和的本质。
片段1:在黑板上画一个三角形,问关于三角形都知道了什么,接着再在三角形中画一条线段,请学生指一指现在这个图形里有几个三角形?
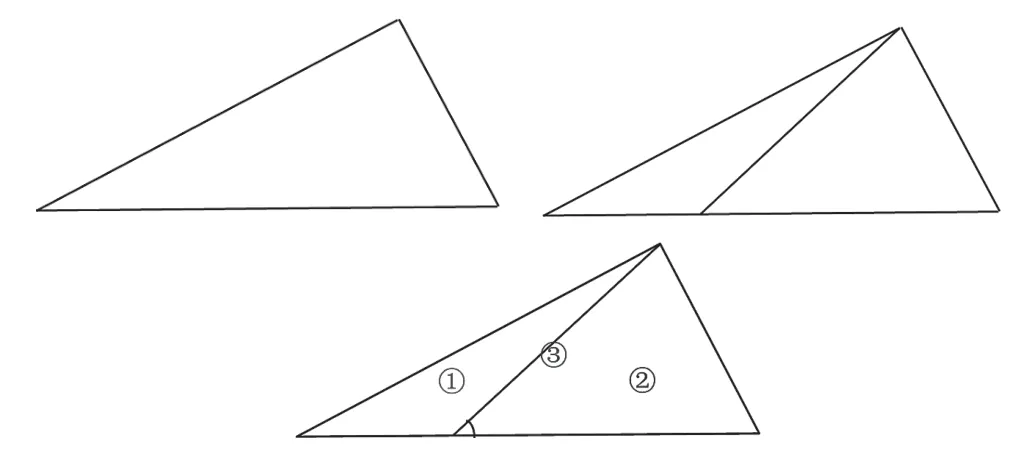
每个三角形的角都在哪儿?
之后让学生辨析这个角是1 号和3 号三角形的角吗?学生明确我们所说的三角形的角不但都在三角形的里面,而且是三角形两条边夹着的角。
顺势揭示概念三角形的内角和概念。
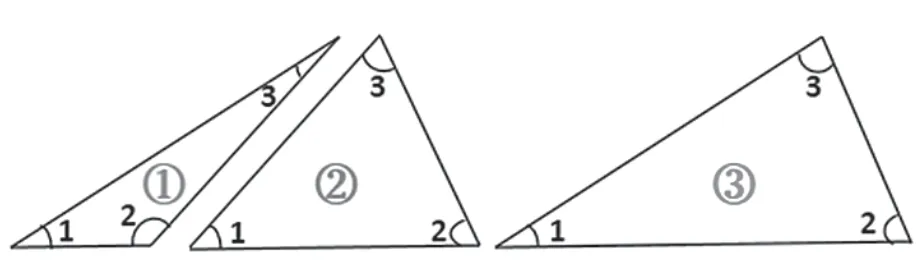
通过这样扎实有效的活动, 为后面的学习扫清障碍,不但进一步加深了学生对角的认识,同时使学习的指向性变得更加清晰,也体现了教师对学情的准确把握和预设。
片段2:有什么方法可以知道这三个三角形的内角和呢? 学生首先想到动手量一量算一算,顺势引导学生合作探究进行活动一。从学生测量数据中发现这三个三角形的内角和大多数是180°,和三角形的大小没有关系,即使不是也非常接近180°,真切感受到测量误差的真实存在性。还有什么方法检验三角形的内角和是180°呢? 老师提前给每人准备一个形状、大小都不一样的三角形,接下来进行活动二。
学生联系平角的知识,用“剪拼”“撕拼”“折拼”等方法,把三角形的内角和转化成一个平角,验证三角形的内角和是180°。通过操作,学生经历了从特殊到一般,从个别到多样的过程, 又通过把三角形内角和转化为平角的探究活动,向学生渗透“转化”数学思想,增强几何直观。
但这还不够,在这个基础上老师又利用计算机中的几何画板引导学生观察数据, 发现无论三角形形状怎样变,但内角和180 度是不变的。
片段3:出示几何画板中的一个三角形ABC,电脑会自动计算出每个角的度数并显示出来,还算出它的内角和是多少度,然后拉动顶点A,三角形的形状发生变化,数据也发生了变化,可内角和还是180°。再拉一拉观察三个角的度数和三角形的内角和。 再换顶点B 顶点C 拉动,重点观察三角形的内角和。
学生很自然地发现三角形的形状在变,三个角却互相牵制,有的角在变大,有的角在变小,但是三角形的内角和没有变化,任意三角形的内角和都是180°。
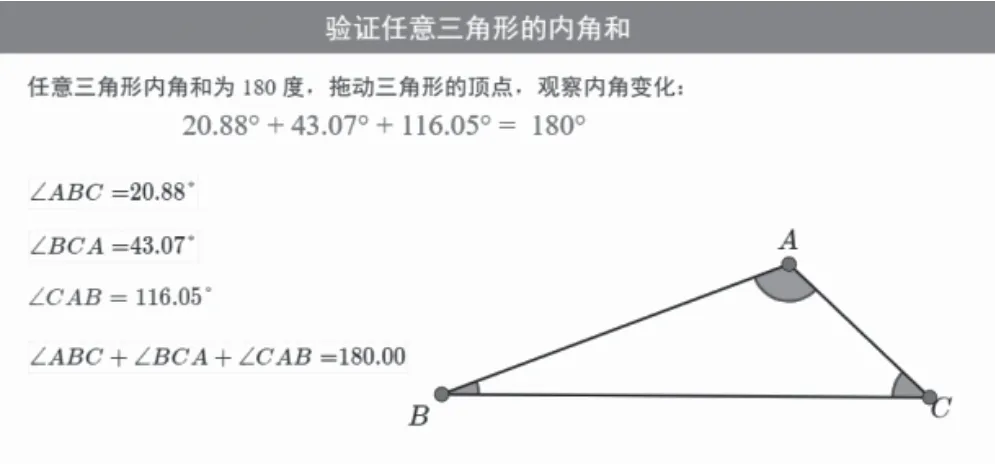
从第二次试讲的课堂来看,学生对于任意三角形内角和是180°这一结论真正做到了在真实情境中经历“猜测——动手实践——得出结论”这一过程。
但是新的问题又出现了,练习题的设计始终和前面的知识不能成为一体,也就是新课标要求教学目标的设定要体现整体性,注重教学内容的结构化,或者在单元视角下,让学生运用三角形的内角和是180°特征解决哪些问题更有效。怎样能够培养学生发现问题和解决问题的能力摆在眼前。 经过进一步思索,联系本单元接下来的内容多边形的内角和, 做到能够关注知识的结构化, 让教学精准启航。
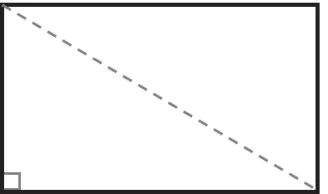
片段4:出示一个长方形,它的内角和可以利用4 个直角乘4 来解决,也可以用对角线把这个长方形分成两个三角形, 三角形的内角和是180°,乘2 也等于360°。
再出示不规则四边形,它的内角和同样可以转化成两个三角形来解决。 五边形、六边形都可以推理转化成三角形的内角和来解决,让学生思维打开,认识一种新的数学方法“推算”。
接着回到课前研究过的三角形,根据这几个已知角的度数求出其他角的度数并发现它们之间有什么关系。这些题目具有较强的综合性, 学生要灵活运用所学知识解题,
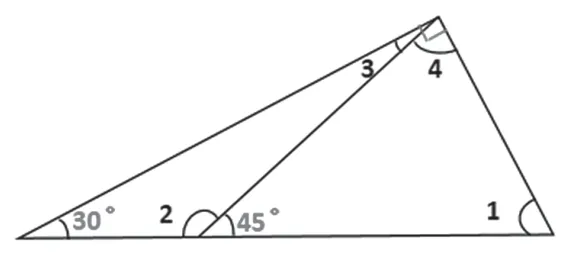
求出每个三角形其他内角的度数既巩固三角形内角和的性质,平角等相关知识,还适度拓展外角的知识,提高思维的有序性和灵活性。
历史是根,文化是土壤,在新课标理念的引领下,在立足学生核心素养培养的今天,教师还要在课堂上传授知识技能的过程中渗透数学史和数学文化。这节课的最后,通过一段小微课,向学生介绍了泰勒斯、帕斯卡等数学家研究验证三角形内角和是180°的故事,以及有趣的转笔验证法,让学生跨越时空了解这些伟大数学家解决问题的策略, 提升自身认知,促进知识的融会贯通。
每一次磨课时领导和同事都能客观地提出存在的问题及改进的意见,在肯定教学大框架的基础上,抠细节,精益求精。 在《黑龙江教育》同课异构活动中,老师的精彩呈现获得了大家的认可。 虽有待改进的地方,但一次次磨课的过程正体现了一名青年教师追求上进的工作态度。
好课锋从“磨课”出,精彩缘自“苦磨”来。 经过了研课磨课,上课教师能精彩演绎打磨后的课堂教学,让每一位教师感受到了“研课”的效果、“磨课”的魅力,真正做到了在研磨中学习、成长。

