设点法与设线法在解析几何中的应用

李亚文

(深圳市横岗高级中学,广东 深圳 518000)

《普通高中数学课程标准(2017年版)》提出:数学运算主要表现为理解运算对象,掌握运算法则,探究运算思路,求得运算结果.通过高中数学课程的学习,学生能进一步发展数学运算能力,有效借助运算方法解决实际问题;通过运算促进数学思维发展,形成规范化思考问题的品质,养成一丝不苟、严谨求实的科学精神.解析几何的研究对象是几何图形,以平面直角坐标系为研究工具,通过代数运算解决几何问题.解析几何作为高中数学中的重要内容,对运算能力有一定的要求,但是在日常的教学和学习中,往往热衷于算,这背离了解析几何的思想.所以在解析几何的教学中,要善于用几何的视角来分析问题,把握几何图形中的变量关系以及图形特征.为此,本文从一些高三复习中的典型问题入手,帮助学生如何更好地使用设点法与设线法来处理实际的问题,提升数学运算能力,发展数学思维,提升核心素养能力.

1 试题呈现

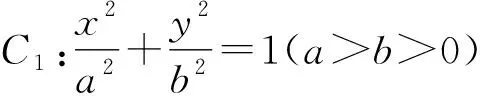
(1)求椭圆C1和抛物线C2的方程;

(2)过点A(-4,0)的直线l与椭圆C1交于M,N两点,点M关于x轴的对称点为E.当直线l绕点A旋转时,直线EN是否经过一定点?请判断并证明你的结论.

2 题目解析

2.1 第(1)问解析

解得p=4,c=1,a=2.

2.2 第(2)问解析

解法1 (设点法)设M(x1,y1),N(x2,y2),E(x1,-y1),

因为A,M,N三点共线,

即x1y2-x2y1=4(y1-y2).

=-(y1+y2).

所以x1y2+x2y1=m(y1+y2)+n(x1-x2).

由上式可得m=-1,n=0.

所以直线EN经过的定点坐标为(-1,0).

化简,得(x1-x2)y+(y2-y1)x=x1y2-x2y1.

所以经过E,N的直线方程可表示为

(x1-x2)y+(y1+y2)x=x1y2+x2y1.

由设点法可知

(x1-x2)y+(y1+y2)x+(y1+y2)=0.

即(x1-x2)y+(y1+y2)(x+1)=0.

直线EN经过的定点坐标为(-1,0).

解法3(设线法)当直线l的斜率不为0时,设其方程为x=ty-4.

(3t2+4)y2-24ty+36=0.

设M(x1,y1),N(x2,y2),E(x1,-y1),

经过E,N的直线方程可表示为

(x1-x2)y+(y1+y2)x=x1y2+x2y1.

化简得(x1-x2)y+(y1+y2)x=(ty1-4)y2+(ty2-4)y1=2ty1y2-4(y1+y2).

代入上式,得

=-(y1+y2).

即(x1-x2)y+(y1+y2)(x+1)=0.

所以直线EN经过的定点坐标为(-1,0).

当直线l的斜率为0时,直线EN恒过定点(-1,0).

解法4 (设线法)当直线l的斜率不为0时,设其方程为x=ty-4.

(3t2+4)y2-24ty+36=0.

设M(x1,y1),N(x2,y2),E(x1,-y1),

所以x1y2+x2y1=m(y1+y2)+n(x1-x2).

化简,得2ty1y2-(m+4)(y1+y2)=n(x1-x2).

所以由上式得

由于x1,x2取值的任意性,当m=-1,n=0时,直线EN经过的定点为(-1,0).

所以当直线l的斜率为0时,直线EN恒过定点(-1,0).

评析解法1中的设点法从图形中的共线问题入手,把题目中的条件进行坐标化表示,通过它的对偶式进行整体变形,从而解决问题.解法2中的设点设线法通过对直线的两点式方程重新建构,得到直线方程的另外一种表达形式,结合设点法,对比得到定点.解法3和解法4中的设线法,采取反设直线的方式,虽然采取直线和曲线联立,但是通过对题目中图形的坐标化表示和建构,通过代数的推理和运算得到结论,从而降低运算量.

设点法是用几个点的坐标作为变量,通过几何图形的坐标化来建立各个变量之间的关系,用代数变形的手段建立目标条件与已知条件的关系,从而解决问题.设线法通过联立方程,用设而不求,整体代换来解决问题[1].

3 性质推广

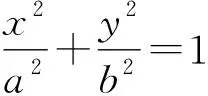
性质3过点P(t,0)作直线交抛物线y2=2px(p>0)于A,B两点,点A关于x轴的对称点A′与点B之间的直线恒过点Q(-t,0),反之也成立.

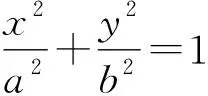
性质6 过抛物线y2=2px(p>0)对称轴上任意一点P(t,0)作一条弦AB,这两点与对应点Q(-t,0)的线段所成角被对称轴平分.

4 性质应用

例2(2019年兰州二模)设抛物线C:y2=2px(p>0)的焦点为F,过点F且斜率为1的直线l与抛物线C交于A,B两点,|AB|=4.

(1)求抛物线C的方程;

(2)若A关于x轴的对称点为D,求证:直线BD恒过定点,并求出该点的坐标.

解析(1)因为直线l的斜率为1,所以直线l的倾斜角为α=45°.

由焦点弦的角度式,得

所以p=1.

即抛物线C的方程为y2=2x.

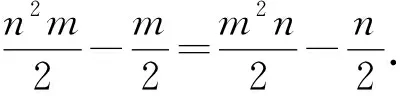
所以mn=-1.

设BD所在的直线方程为

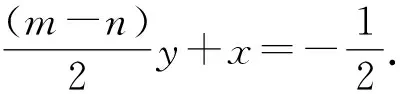
即(m-n)y+(2x+1)=0.

在解析几何的高考复习中,提升运算能力不仅仅是从代数角度入手,教师还要善于引导学生从几何图形中找到关键特征,对常见的图形进行系统性的归纳,把握问题的本质,选择合适的方法,这样才能做到优化运算,提升能力[2].在日常教学中,以坐标法作为核心和纽带,引导学生从数形结合的角度来看待问题,采取设点法和设线法等解决问题的简便手法,也是培养学生直观形象和数学运算的措施.