基于二叉树结点优化的矩形装箱纹理优化方法

马东岭朱悦凯李铭通

(山东建筑大学测绘地理信息学院，山东 济南 250101)

0 引言

实景三维模型可以推动城市数字化、智慧化发展，其建模技术在完善智慧城市空间数据体系中具有重要作用[1]。 当前，基于倾斜摄影的大场景实景三维建模技术发展迅速，模型的数据量也在飞速增加。 随着多源数据融合建模技术的不断发展[2]，在构网阶段会建立更加精细的白模，生成数量更多的三角面元，而每个面元都会对应一个碎片化纹理；同时，相机配置的发展提高会取得更加真实丰富的纹理信息，随之而来的就是单个纹理文件数据大小的增加。 因此，在纹理映射阶段要处理数量更多、单个纹理大小更大的纹理文件。 在纹理映射的过程中:(1) 通过坐标确定有效纹理的区域，利用这种纹理单体化的方式除去了大量的冗余纹理；(2) 通过建立面元最小外接矩形角点的纹理坐标、影像坐标与物方空间坐标之间的联系，将纹理映射到三维模型表面上[3]。 若是对海量的碎片化纹理不加处理直接渲染，则会占据大量内存资源。 而如果封装和优化碎片化纹理，则可以减轻CPU 负担，减少磁盘读写次数，并充分利用GPU 的批处理能力，减轻内存和磁盘的存储负担。 因此，如何将碎片化纹理更加充分地打包和封装，成为当前实景三维建模技术中纹理优化的重要研究问题。

针对此问题，将碎片化纹理打包封装的问题转化为二维矩形装箱问题，即将若干离散矩形按一定规则放入某一较大的已有矩形容器，使得容器的空间利用最大化。 早期一些学者采用了优先左下角的方法(Bottom－Left，BL):BAKER 等[4]采用的BL 方法通过尽可能向下、向左地顺序放置每个矩形；HOPPER 等[5]提出在许多不同的矩形序列上执行基于BL 的启发式算法并选择最佳结果，其可称为左下递减(Bottom－Left－Decreasing ，BLD)；郑巧仙等[6]改进了左下角定位模型，提出了可旋转的二维矩形装箱模型。 这一方法虽实现较为简单，但其无法充分利用矩形容器的空间，装箱效果有待进一步改善。

另一种常见的方法是基于某种最佳拟合度量(Best Fit，BF)选择矩形及其位置，而不是对左下角的位置优先级排序。 BURKE 等[7]提出了包括一系列优先权规则的最佳拟合方法，其会在矩形列表中搜索更好的矩形优先存放；马康等[8]提出了一种改进的最低水平线搜索算法，通过判断排样中产生废弃空闲区域的位置关系，对邻接的空闲区域有效的合并，并结合分布估计算法求解矩形件排样优化问题；TAM 等[9]利用最小自由度优先方法，依次填充边界区域内的空白“角落”—空白空间的边界线—其他空白区域；梁利东等[10]基于多目标优化的择优匹配启发式方法，先定义排样空间和匹配值，计算入排零件与排样空间的宽、高匹配值，再建立统一的多目标优化函数模型，并根据目标函数值的大小确定排放优先规则。 但是这一方法会产生很多难以利用的内部碎片。

为了避免陷入局部最优，也有一些学者尝试了几种元启发式方法[11－13]:WEI 等[14]利用最小浪费优先(Least Wasted First ，LWF)策略，评估矩形所使用的位置，再引入随机局部搜索以改进搜索结果；尚正阳等[15]提出了一种改进的最优剩余空间算法，采用贪婪策略作为最优放置策略，矩形的面积越大、其放置坐标越小，则越优先将其存入；WEI 等[16]研究了贪婪启发式的装箱算法，用一组水平线表示当前的装箱状态，每段水平线的左端点或右端点为坐标点，将小矩形按顺序放置在大矩形中，使矩形的左下角或右下角接触坐标点，每次放置矩形后更新上界线和坐标点，但这种方法在矩形数量较少时效果一般；陈其赛等[17]在方法[16]的基础上，引入带适应度值的skyline 装箱策略，改进了禁忌搜索－遗传混合算法；SCOTT[18]提出了一种基于二叉树的矩形装箱方法，在放入一个矩形后将剩余空间划分为两个子结点，并判断下一个矩形能否放在这些结点所代表的矩形空间中。 这种方法在少量离散矩形的装箱问题中空间利用率比上界线算法更高，但是在大量矩形的情况下会优先选取面积较大的位置，造成空间利用率的浪费；朱庆等[19]采用基于最大接触长度的矩形装箱算法，使矩形存入后与剩余空间接触长度最长，但需不断计算存入矩形与剩余空间的接触总长度；翁其强[20]基于自由域分割的最大矩形装箱算法，在存入矩形后使剩余边长最短，但其在每次插入新的矩形后都须考虑新矩形对剩余空间的扰动，在算法上均较为复杂；王晓坤[21]采用了先利用最大矩形纹理面积与其余矩形纹理面积的差计算容器面积再进行矩形存放的方法，但没有考虑剩余空间分割后放置的顺序，会造成容器空间的浪费。

综上所述，基于BL 的二维矩形装箱算法没有考虑矩形存入顺序，基于BF 的算法对于矩形存入后容器的剩余空间没有合理利用，而其他一些元启发式方法对于剩余空间被访问的顺序没有处理，因此都对矩形装箱算法的空间利用率产生了一定影响。 文章以纹理数据处理中的纹理合并为重点，针对上述方法存在的问题，在二叉树矩形装箱算法的基础上改进，优化二叉树结点数组，按照矩形的面积从大到小作为存入顺序，对于矩形存入后的剩余空间按照合理的面积比最大原则分割，并优化了剩余空间被访问的顺序。 文章开展了一系列的实验验证此种方法的效果，以期解决矩形优先被存放在容器中对角线位置而造成的空间浪费问题，进一步提升容器的空间利用率，使得三维建模在纹理映射的过程中可以更加高效地对大量的纹理进行操作，减少了内存资源的浪费。

1 二维矩形装箱纹理优化方法

文章提出的基于二叉树结点优化的二维矩形装箱纹理优化方法主要可分为预处理、矩形存放和结点数组优化等3 步。 整体流程图如图1 所示。

图1 整体流程图

1.1 预处理

二维矩形装箱方法中的预处理即对二维矩形组成的数组排序。 在影像被加载后，通过影像的纹理坐标与三维模型的坐标确定纹理的有效区域，去除整张影像中无用的冗余区域，得到纹理碎片。 由于从影像中获取的纹理碎片是杂乱无序的，如果按照其本来的顺序存放，会降低纹理集的空间利用率。二维矩形存入容器示意图如图2 所示。 将待装箱纹理矩形存入矩形容器中，图2(a)为未经过预处理存入示意图，其存入顺序为b－>e－>c－>d－>a；图2(b)为预处理后的存入示意图，其存入顺序为e－>d－>c－>b－>a。 可以看到，在图2(a)中，由于矩形存入顺序混乱，空间利用不合理，导致矩形a 无法存入容器；而图2(b)中5 个矩形可以全部被存入容器。 因此，为了避免二维装箱过程中产生插入冲突而影响算法结果，在装箱前要将所有待装箱矩形纹理按一定规则排列。 常用的排序方式有高、宽、面积、周长。文章通过对比4 种排序方法实验可知，按照矩形的面积排序的容器空间利用率最高。 设矩形数组I ＝{r1，r2，…，rn}、ri ＝{xi，yi，wi，hi} ，其中xi、yi为矩形i左下角坐标；wi、hi分别为矩形i的宽、高，pixel。采用快速排序的方法，排序后的数组应满足表达式，由式(1)表示为

图2 二维矩形存入容器示意图

1.2 矩形纹理存放

给定一个按照面积大小排序的矩形纹理组成的数组，将其依次存入一个矩形纹理集中。 文章中的矩形纹理集R定义由式(2)表示为

式中x和y分别为矩形纹理集左下角的坐标；w和h分别为矩形纹理集的宽度和高度，pixel。

所研方法采用了二叉树的思想，原始容器为根结点，给定一系列小矩形I ＝{r1，r2，r3，r4，…}，在一个矩形ri存放进去后，剩余空间可以划分为2 个较小的矩形区域，即为两个子结点S和L，分别表示面积较小、较大的空间。 矩形①存入容器后示意图及其对应二叉树结构图如图3 所示。 可以看出，剩余空间可以分割成A、B 两部分。

图3 矩形①存入容器后示意图及其对应二叉树结构图

接着存入下一个矩形②，将其存入后子结点继续向下分为新的子结点。 矩形②存入容器后如图4(a)所示，将矩形②存入结点A，并将结点A 的剩余空间分成C 和D；其二叉树结构如图4(b)所示。

图4 矩形②存入容器后示意图与其对应二叉树结构图

在对剩余部分分割时，需遵循一定的规则使容器的空间利用率更高，即分割后两个空间的面积差最大。 图5 表示将矩形①存入容器后两种不同的分割方法。 假设矩形①存入容器后，容器的剩余宽rw和剩余高rh的关系为rh < rw，则通过推算可知新生成的4 个空白矩形空间A、B、A′、B′中，矩形空间B 的面积最大。 因此，图5(b)可以获得更大的空白区域来存放更大的矩形，对提高容器的空间利用率有一定的帮助。

图5 对剩余部分的两种分割方法图

为了达到这种效果，在存放进一个矩形后，可判断其剩余空间的边长。

设矩形存入容器后剩余宽度和剩余高度为rw、rh，并由式(3)表示为

若rh < rw，则新生成的矩形空间可由式(4)表示为

否则，由式(5)表示为

式中xnode、ynode、wnode、hnode分别为当前结点代表空间的x、y坐标以及宽高，pixel。 在实际纹理合并过程中，在当前矩形纹理被存入纹理集后，剩余的空间将按照上述规则可分割成两部分，并生成代表这两部分的新结点。 而结点数组中删除了代表当前空间的结点，存入新生成的结点。 为了优先利用面积较小的区域，从而充分利用纹理集的空间，文章在当前矩形纹理存放完后优化了结点数组，再存放下一个矩形纹理。

1.3 结点数组优化

常规的二叉树矩形纹理合并方法利用一个数组存放所有的空白结点，每次存入一个矩形纹理之后，将当前结点弹出数组，再将新生成的两个子结点存入数组的末尾。 在下一个矩形存放时，判断数组中最后一个结点是否可以存入，若存放不下则判断倒数第二个结点，以此类推。 由于新生成的空间多为面积较大的对角线位置，因此矩形会优先存入这些位置，而边界处的空间往往不会被迭代到，造成空间浪费。

为了解决这个问题，文章在此方法基础上改进，在下一个矩形存放前对结点在数组中的排列顺序优化处理，按照结点所代表空间的面积从大到小排序，这样数组末尾位置的结点代表的就是面积最小的空间，即整个容器的边角处区域。 在存放时优先将矩形存入面积最小的空间，使这些面积较小的空间可以得到充分利用。 当矩形纹理r存入时，对结点数组从后向前遍历，第一个能满足Si < Sr的结点i所代表的空间即为该矩形纹理存放的位置。 如图6 所示，将结点数组[A，C，B]按照结点A、B 和C 所代表的空间面积大小顺序重新排序，排序后为[C，B，A]。 在下一个矩形存入时，先对结点A 判断，若A存放不下则判断结点B，以此类推。 这种方式充分利用了纹理集的空间，也避免了原本面积较大的结点被分割得更加破碎，进而提升了整个纹理集的空间利用率，使纹理合并的效果更加紧凑。

2 实验与分析

2.1 实验数据与实验环境

为验证文章提出的基于二叉树结点优化的二维矩形装箱方法的有效性，利用程序随机生成若干矩形，并设置两组实验分别对大量矩形和少量矩形两种情况进行装箱效果测试。 第一组实验生成150 个矩形，其长、宽尺寸为<600 的随机整数；第二组实验生成5 000 个矩形，其长、宽尺寸为<100 的随机整数。 设定容器尺寸均为4 096 pixel × 4 096 pixel。(1) 验证1.1 节对矩形所采用的排序方式的合理性；(2) 验证1.2 节中剩余空间分割规则对整个装箱结果的影响；(3) 通过对比实验的方法验证所研方法在矩形装箱中效果的提升。

文章采用C＋＋作为开发语言，在Visual Studio 2019 开发平台上实验。 实验系统微机硬件配置如下:CPU，Intel(R)Core(TM)i7－6700 CPU ＠3.40 GHz；内存，8.00 GB；显卡，NVIDIA GeForce GTX 1060 3 GB。

2.2 对矩形排序方式的对比

利用程序随机生成的150 和5 000 个矩形，将其存入一个长、宽均为4 096 的容器中，分别采用不排序以及按照宽、高、周长、面积排序的方式。 计算5 种排序方式的空间利用率，见表1。

由表1 可知:对于150 个的少量矩形而言，不对矩形预处理最后的空间利用率为89%；对矩形预处理后空间利用率有不同程度的提高，其中按照矩形面积排序时空间利用率可达95.5%，比不排序提高了6.5%。 当矩形数量增加至5 000 个时，不进行预处理的空间利用率为88.6%；如果按照矩形的宽、高或周长来排序会造成空间利用率的降低，而按照面积排序的预处理方式可以得到最高的空间利用率为91.3%，比不排序提高了2.7%。 由此可知，在对矩形预处理时，按照矩形面积排序可以达到最高的空间利用率。 另外，矩形的预处理对于装箱效果的提升对少量矩形来说更为明显。 5 种排序方式的装箱结果如图7 和8 所示。

由图7 和8 可知，不论矩形的数量多少，前4 种方式都不同程度地出现了剩余空间不齐整的情况(箭头处)。 而按照矩形的面积排序可以最大程度地利用容器的空间，使得剩余空间可以更加高效地存放更多的矩形。

2.3 剩余空间分割对比

对1.2 节中的当前矩形存放完毕后剩余空间的分割规则实验验证，对比分析了是否使用该规则的装箱效果，实验结果如图9 所示。 图9(a)和(b)为不使用分割规则的装箱结果，图9(c)和(d)为使用分割规则的装箱结果。

图9 分割规则对装箱结果的影响图

由图9(a)和(b)可以看出，若不使用该分割规则，后续的矩形在存入容器时会优先在上一矩形所在横排存放。 这就导致该横排上部的空间分割得更加破碎，后续没有矩形能够存入该区域，造成了空间上的浪费。 而由图9(c)和(d)可以看出，采用所提空间分割规则可以对剩余空间有效地规划，在分割时尽可能地保留了更加完整的空间，在存放时有效利用了后续矩形。

使用分割规则和不使用分割规则实验后得到的空间利用率见表2。

由表2 可知，相较于不使用分割规则，使用分割规则对于装箱空间利用率分别提升了约40%和46.5%，并均提升了近1 倍。 因此，剩余空间的有效分割对于最后的装箱结果有着重要作用。

2.4 装箱效果对比

为证明所研方法中对结点数组的优化在矩形纹理装箱过程中的作用，利用Scott 提出的Binary Tree装箱方法[18]与所研方法对比分析。 装箱结果如图10 所示。

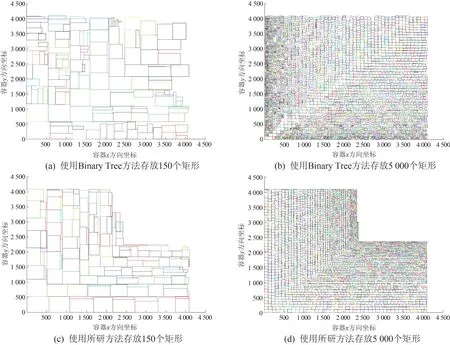
图10 两种装箱方法的装箱结果图

图10(a)和(b)是Binary Tree 方法的装箱结果，可以看出，面积更大的矩形更优先存放在容器对角线的位置上，而这会导致剩余空间的破碎化，不利于后续矩形的存放。 图10(c)和(d)为所研方法对剩余部分结点数组优化后的装箱结果，可以看出，矩形在存放的时候更优先存放于容器的边上，可以更加有效地利用容器的空间。 两组实验结果说明，针对于少量矩形和大量矩形，所研方法的装箱效果均优于Binary Tree 方法。 两种装箱方法在不同矩形数量实验中的空间利用率和效率对比表见表3。

表3 两种装箱方法的装箱空间利用率与效率对比表

由表3 可知，相比于Binary Tree 方法的空间利用率，所研方法分别提高了11.7%和16.2%，其值可达90%以上。 在效率方面，当模型纹理数量较少时，两种方法在耗时方面相当，但是由于所研方法增加了剩余结点排序的步骤，因此在纹理数量非常大时会造成装箱效率降低。 然而，相比于Binary Tree方法，所研方法主要优化了纹理集边缘空间的利用，因此能够提高装箱的空间利用率，可以使矩形容器存入更多的矩形，相同数量的纹理可以打包成更少的纹理集，进而减少了三维重建纹理映射过程中的读取操作次数，减轻了内存和磁盘负担。

2.5 倾斜影像数据实验效果对比

为了验证所研方法在倾斜影像实际应用中的效果，文章结合实际二维纹理数据实验验证了纹理打包过程。 文章选取长春市长春公园的部分倾斜影像数据，该数据使用大疆精灵4P 无人机搭载5 镜头采集，单幅影像的像幅大小为5 456 pixel×3 632 pixel。 通过Context Capture 软件获取了139 个碎片化纹理文件，分别采用文献[18]方法和所研方法进行纹理打包:(1) 批量读入碎片化纹理，提取纹理的宽高信息，生成矩形纹理数组；(2) 利用所研算法纹理合并，生成矩形纹理左下角点在纹理集中的坐标并存入矩形纹理数组；(3) 利用OpenCV 库将其合并到一张纹理集上并输出。 两种方法生成的纹理集效果图如图11所示。

图11 两种方法生成的纹理集效果图

由图11 可以看出，由于Binary Tree 方法更优先将纹理存入纹理集的对角线位置，因此造成了在纹理集边界位置的空间浪费。 相比于Binary Tree 方法，所研方法会优先选择边界位置的空间，使整个空间利用得更加合理，相同数量的纹理经过打包后节省了约50%的空间。 因此在纹理集文件大小方面，Binary Tree 方法生成的纹理集文件大小为1.16 MB，而所研方法生成的纹理集文件大小仅为0.88 MB，缩小了约35%，节约了磁盘空间。 而在装箱效率方面，Binary Tree 方法和所研方法耗时分别为0.025、0.022 s，表明在矩形纹理数量不多时，两种方法耗时相当。

综上所述，所研方法与Binary Tree 方法相比，在矩形数量合适的情况下两种方法的效率相当，而所研方法在边缘利用方面更具优势，能使矩形容器的边缘空间得到充分的利用，提高了整体的空间利用率，装箱后的纹理集文件大小显著减小，节约了磁盘空间，减轻了后续读写处理的内存压力。

3 结论

针对目前三维建模纹理映射过程中碎片纹理磁盘读写的优化问题，文章以纹理数据处理中的纹理合并为重点，提出了一种基于二叉树结点优化的二维矩形纹理装箱方法。 经研究得到的主要结论如下:

(1) 在碎片化纹理合并之前对其排序预处理可以避免因顺序混乱而导致的插入冲突，其中按照矩形面积排序的方法效果最好，与不排序直接纹理合并相比空间利用率提高了约5%。

(2) 在矩形存入后对剩余空间按照面积差最大的原则分割可以使纹理合并的空间利用率提高约1 倍。

(3) 相较于传统的基于二叉树的纹理合并方法，文章侧重对纹理集的边缘空间利用。 无论对于少量矩形还是大量矩形，通过对二叉树结点数组的优化均能使纹理合并的利用率提高>10%，而合并后的纹理集文件大小也可缩小35%，为后续纹理重映射过程中的磁盘读写和内存减轻了压力。