屈曲约束支撑核芯板在常幅加载下的高阶屈曲演化研究*

解崇白,杨晓东,张世凯

(1.昆明理工大学建筑工程学院 ,云南 昆明 650504; 2.云南省工程抗震技术研究中心,云南 昆明 650504)

0 引言

近年来,减隔震技术中的被动减震装置越来越多地被作为结构减震隔震的第一道防线,被动减震装置在地震输入后进入工作状态,在滞回变形过程中吸收耗散地震输入的能量,从而减轻因结构非线性变形对结构关键部位产生的耗能负担。屈曲约束支撑(BRB)作为被动减震装置的一种,目前已经在日本、美国等地被广泛研究和采用,我国学者也对BRB进行大量研究,并得到了丰富的研究成果[1]。

屈曲约束支撑在往复荷载作用下,发生滞回变形后主要破坏形式为低周疲劳破坏。早在1912年,Kommers[2]通过系列循环弯曲试验,得出循环挠度是低周疲劳研究的一个重要因素。随后Orowan[3]提出了关于循环应变描述疲劳寿命的表达式。在此基础上,Coffin[4]进行了修正和深入研究,提出Manson-Coffin公式。2010年日本学者Tsutomu等[5]对5个BRB试件进行拉压循环加载试验,针对性地提出了预测低周疲劳强度的Manson-Coffin型经验方程。2013年,黄波等[6]对国标Q235钢屈曲约束支撑进行低周疲劳试验,试验得出核芯板多波屈曲是导致屈曲约束支撑的低周疲劳性能小于核芯板低周疲劳性能的主要原因;2014年,陈可鹏等[7]对国产Q235芯材屈曲约束支撑进行疲劳试验分析,常幅加载制度下BRB疲劳寿命可用应变与循环圈数表征的Manson-Coffin理论公式表达,通过雨流计数法提出了随机地震荷载下的累积损伤评估;2017年,陈可鹏等[8]对屈曲约束支撑的低周疲劳性能进行研究,发现等幅加载下屈曲约束支撑疲劳寿命与应变满足Manson-coffin公式。2018年,Hoveidae[9]采用新建立的循环空洞生长模型(CVGM)对核芯板断裂和裂纹萌生进行理论预测。

目前针对BRB类金属阻尼器疲劳寿命问题往往基于试验基础建立预测模型,并通过试验检测评价疲劳寿命指标。然而,当前对于BRB在低周疲劳下的破坏研究较少,尤其是关于屈曲过程中裂缝扩展机理演化的研究,对于核芯钢材应力应变损伤研究是非常重要环节。通过对3组一字形钢管混凝土屈曲约束支撑试件进行不同加载制度下拟静力试验,根据得到的滞回曲线和骨架曲线结合构件不同破坏现象对BRB形变过程中核芯板裂纹萌生、扩展过程进行理论研究。同时通过对BRB核芯板高阶屈曲变形进行理论推导和演化,得到屈曲半波数随芯板厚度增加而逐渐减小的推论,同时根据局部应变集中产生原理,发现间隙与核芯板厚度之比与应变集中呈正相关,为装配式BRB疲劳设计及工程应用提供必要理论支撑。

1 BRB试验概况

1.1 构件参数

BRB试件为一字形钢管混凝土约束屈曲耗能支撑(见图1),核芯板板材为Q235B,过渡段为焊接十字形,总长度均为4 000mm,屈服长度比约0.6。核芯板与约束混凝间隙黏结采用1.5mm或2mm厚SBS改性沥青防水卷材。构件为全尺寸无缩尺模型构件,其与实际应用参数相近。

图1 试验构件模型

试件编号分别为BRB-1,BRB-2,BRB-3,核芯板材料参数如表 1所示。整体设计及力学参数如表2所示。其中,构件屈服长度比为屈服耗能段与屈曲约束支撑总长度比值,可衡量有效耗能长度。

表1 核芯板材料参数

表2 试件设计参数

表3 BRB屈服情况统计

1.2 加载方案

由于核芯板屈曲阶数受到加载幅值影响,且随着加载幅值增大,累积塑性变形逐渐提高,核芯板塑性损伤加剧,影响芯板在屈曲过程中的演化。参考JGJ 297—2013《建筑消能减震技术规程》[10]和DBJ/CT 105—2011《TJ屈曲约束支撑应用技术规程》[11]进行加载,BRB-1在L/300,L/200,L/100逐级加载各3圈后(L为支撑长度),随后保持在L/100幅值下加载直至破坏,以研究大应变下芯板在屈曲过程中的屈曲演化和疲劳寿命。BRB-3采用同样逐级加载,随后在等级加载完后在加载级为L/100情况下分别受拉、压单向循环加载各3圈,接着在L/150幅值下进行疲劳加载60圈,最后以逐级极限式加载至构件破坏,以研究单向拉压对核芯板屈曲演化及疲劳寿命的影响。BRB-2以JG/T 209—2012《建筑消能阻尼器》[12]基本加载等级先后进行2次加载,随后在Δbd幅值下进行疲劳加载60圈、1.2Δbd加载30圈,最后在1.5Δbd幅值下加载直至破坏,以研究同一加载等级序列先后加载的核芯板屈曲变化及疲劳寿命情况。

2 试验结果与分析

2.1 试验现象

试验设备如图2所示。BRB-1破坏现象(见图3a)说明芯板中间截面成为受力过程中演变的集中段,在循环往复加载中发生大变形低周疲劳,最终拉伸断裂。BRB-2芯材整体试验中出现了整体多波屈曲,具有明显波峰和波谷,屈曲起伏位移约为2mm,同时在靠近过渡段约200mm处发生了疲劳断裂破坏,断裂截面附近出现未贯通短裂纹,如图3b所示。而BRB-3断裂截面为斜截面(见图3c),说明芯板仅出现一阶模态屈曲,其在中部截面的一阶屈曲背面出现裂缝后断裂,同样为低周疲劳破坏。

图2 加载装置

图3 试验破坏现象

2.2 骨架曲线

参照等效耗能原理提取试件屈服点,计算结果如表 3所示。3个试件骨架曲线如图4所示。从BRB-1骨架曲线(见图 4a)可以看出,在初始加载段有明显屈服段平台。BRB-2在首次等级加载与第2次等级骨架曲线(见图 4b)拉伸状态下出现重合,而受压状态不重合。BRB-3骨架曲线中(见图 4c)则无明显屈服段平台。

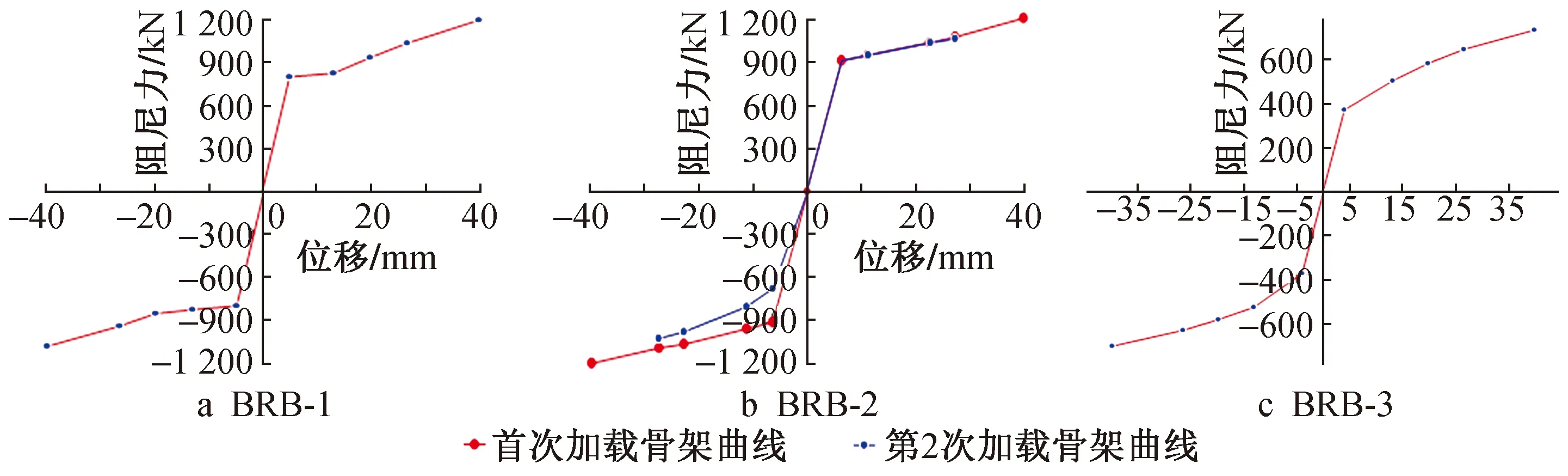
图4 3个试件骨架曲线

2.3 滞回曲线

3个试件滞回曲线如图5所示,图中阻尼力即为构件内力。3个试件滞回曲线由于钢材循环应变硬化,阻尼力有所提高,导致构件失效前滞回曲线均无明显捏拢现象。

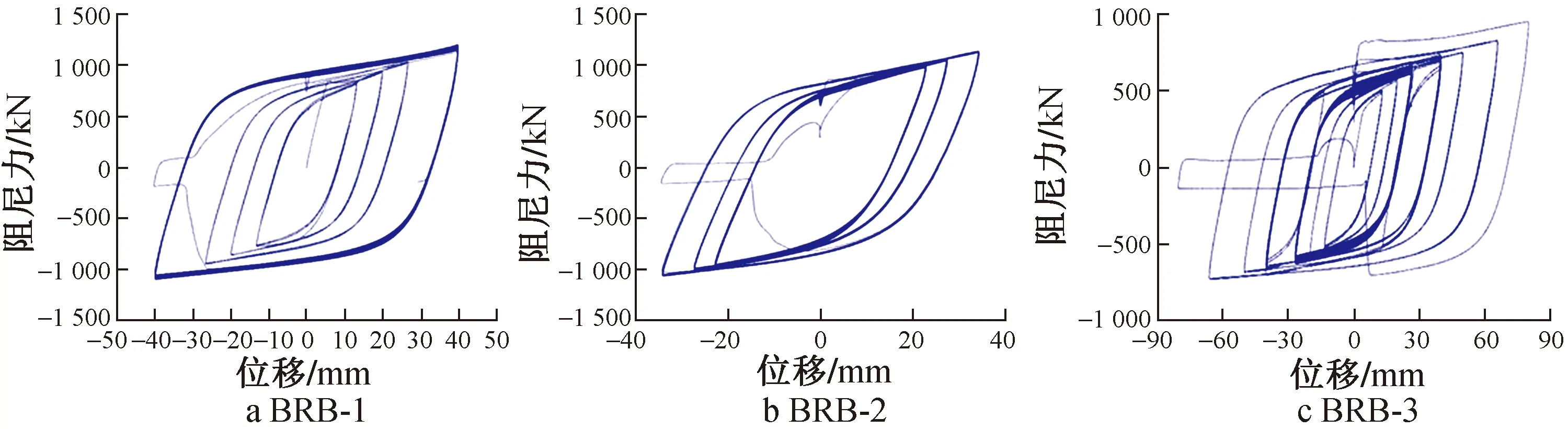
图5 3个试件滞回曲线

3 核芯板对低周疲劳寿命的影响分析

Takeuchi等[13]研究了BRB核芯板高屈曲模态,表明芯板局部屈曲导致核芯板纵向应力应变分布不均导致 BRB累积变形能力下降。

3.1 屈曲约束支撑失稳形态

核芯板失稳形态如图6所示,在设计合理下(见图6a),核芯板则以微波屈曲形态进行往复塑性变形,核芯板所产生的屈曲波弧曲率较小,屈曲弧段不会出现应力集中现象。对于间隙控制过大情形(见图6b),轴向受压时产生较大屈曲变形,与约束单元接触的截面处产生应力集中,易产生疲劳破坏,导致失效。图6c,6d分别属于整体失稳与局部过度失稳情形,设计需规避这类破坏形式。

图6 屈曲约束支撑失稳形态

3.2 核芯板高阶屈曲演化过程

当核芯板在轴向压力达到临界稳定承载力后发生一阶正弦半波形态失稳。随着轴向压力的加大,芯板将依次发生二阶、三阶及多阶变形模态,如图7所示。但当芯板达到一定多阶模态后便趋于稳定,不再继续发生更高阶模态。

图7 高阶屈曲演化

3.3 高阶微幅屈曲元段分析

以一字形核芯板进行理论分析,将端部假设为铰支约束情况,核芯板在受压时,长度变化量Δl由屈曲收缩引起变形长度减小量Δlq和轴向变形长度ls两部分组成。即:

Δl=ls+Δlq

(1)

Δlq=ls-l1=ls+Δl-l0

(2)

式中:l0为耗能段原始长度;l1为压缩后屈曲形态直线长度;ls为压缩后屈曲形态曲线长度。

屈曲半波计算长度为[14]：

(3)

式中:tc为芯板厚度;σcy为芯板屈服应力;Et为钢材料切线模量。

对于屈曲后长度ls可根据几何近似求解得:

(4)

式中:s为核芯板与约束内壁间隙宽度;n为正弦屈曲半波数。

引入屈曲演变系数f,可通过式(5)计算:

(5)

(6)

通过式(6)绘制正弦屈曲半波数与应变幅值、核芯板厚度间关系,如图8所示。由图8可知,屈曲半波数随着加载幅值逐渐增大后趋于恒定值;屈曲半波数随着核芯板厚度增加逐渐减小,反之则增加。

图8 屈曲半波数与应变幅值关系

考虑屈曲内芯挠曲线为正弦波(见图9)可得:

y=ssin(πx/lp)

(7)

根据力分解,可分为水平向及垂直向平面力问题[14](见图10),平衡方程:

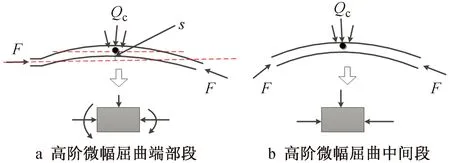
图10 高阶微幅屈曲元段受力示意

Qc=2Fxtanθ

(8)

式中:Fx为F水平分力;Qc为内壁挤压力。

联立式(3), (7),(8),内壁挤压力Qc可计算:

(9)

式中:s为屈曲约束核芯板与约束单元间隙。

通过推导表明,影响失稳的重要参数为间隙值s与上屈曲半波长度lp的比值。当比值较大时,挤压力变大,应力集中也随之变大,疲劳寿命降低。而当间隙较小时,芯板难以发生高阶微幅屈曲变形,导致芯材三向应力挤压,难以耗能。因此,间隙应设置理论合理值,对芯板应力集中和低周疲劳寿命有着重要影响。

3.3 间隙与核芯板厚度之比对局部应变集中的影响

Matsui等[15]提出了BRB芯板应变集中比指标,该指标可表示为:

(10)

(11)

联立式(10),(11)可得应变集中比简化计算式:

(12)

可见αc为s/t函数,Usami等[16]研究指出d/t建议<1.2,因此s与d可近似替换。同时省略高阶量,式(12)为:

(13)

Wang等[17]讨论指出若假设Et=0.025E,则材料低周疲劳寿命可近似反映局部应变范围的BRB低周疲劳寿命。因此,可近似取切线模量为0.025E调整讨论计算。

在核芯板材料一定情况下,对αc进行单一变量分析。假定芯板屈服力与所用材料屈服力相差不大,则屈服力一定;屈服后的塑性滞回圈切线模量取0.025E。其他参数参考合理范围选择,可对s/tc进行变量影响分析,如图11所示。由图11可知,应变集中系数αc与s/tc(间隙与核芯板厚度之比)呈正相关。因此,间隙与核芯板厚度之比是屈曲约束支撑设计的关键参数。

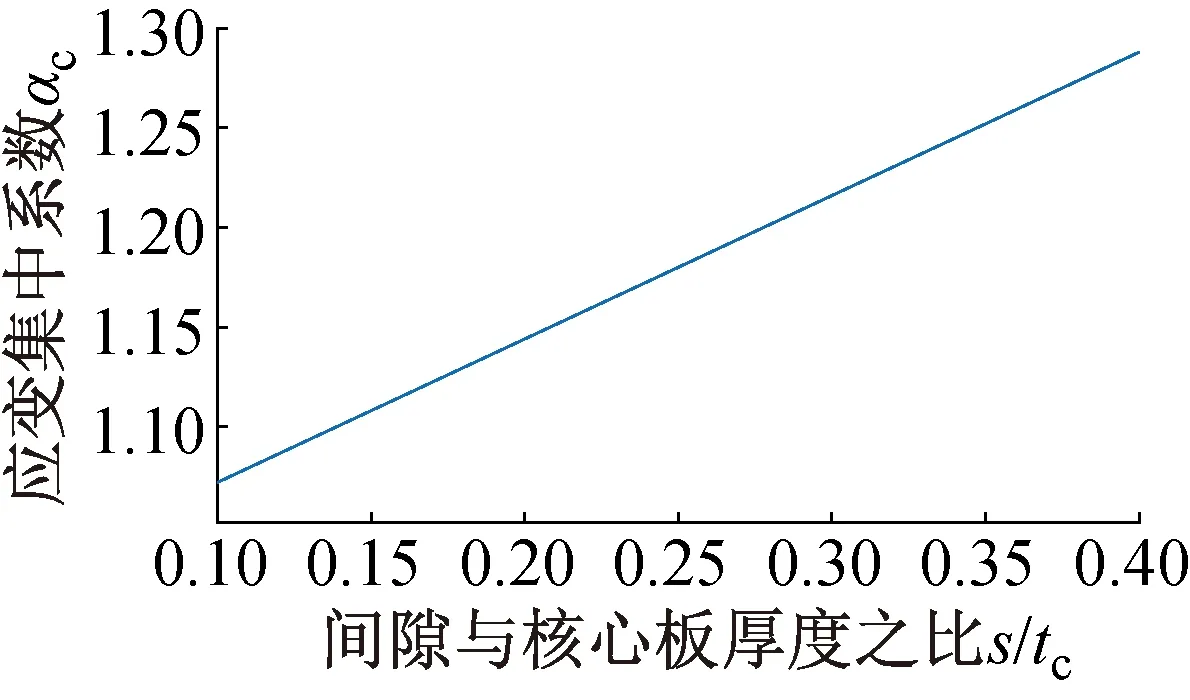
图11 间隙与核芯板厚度之比对应变集中的影响

4 结语

本文对屈曲约束支撑3个全尺寸试件进行拟静力往复加载试验,根据试验所得数据与设计参数进行对比验证。对BRB核芯板高阶屈曲变形演化进行理论推导,以及高阶屈曲变形中间隙与核芯板厚度之比对应变集中的影响进行分析,得到以下结论。

1)该类型BRB滞回曲线饱满,无捏拢效应,疲劳寿命较好。同时极限加载表明,具有极好的延性,完全满足在大震动下层间位移角限值下的最大位移需求。

2)BRB屈曲半波数随着加载幅值逐渐增大后趋于恒定值且屈曲半波数随着核芯板厚度增加逐渐减小。

3)核芯板和约束构件间隙与核芯板厚度之比与核芯板局部应变集中呈正相关,在设计中应考虑间隙与核芯板厚度之比取值。