新型延性装配式防屈曲钢支撑的滞回性能分析

陈 浩， 孙国华， 杨伟兴

（1.苏州科技大学 土木工程学院，江苏 苏州215011； 2.中衡设计集团股份有限公司，江苏 苏州215123）

普通钢支撑在强烈地震下往往因受压屈曲导致轴向承载力、变形及耗能能力急剧降低，致使结构破坏。目前，工程界通常会采用防屈曲支撑提高其变形及延性行为。防屈曲钢支撑（Buckling-Resistant Brace，BRB）由核心单元和外围约束单元构成，核心单元承受轴向拉、压力，外围约束单元可抑制核心单元屈曲，确保其在轴力作用下仅发生屈服[1-2]。 在正常使用阶段及多遇地震作用下，BRB 支撑同普通钢支撑一样，提供足够的抗侧刚度和水平承载力。 在罕遇地震作用下，BRB 支撑通过充分发展塑性，有效耗散地震输入能量，避免主体结构遭受严重损伤。

近年来，BRB 支撑成为了结构抗震研究领域的热点，各国学者提出了许多形式新颖、性能优良的构造设计与截面组成方式，并对其滞回性能[3-5]、疲劳性能[6-7]和稳定性能[8-9]进行了大量研究。 已有的研究主要侧重于BRB 支撑整体的稳定性能和滞回性能等方面，就其破坏模式来看，其塑性区域一般都集中在核心单元的某个集中位置，致使变形能力偏低。 周云等提出了定点屈服BRB 支撑[10-11]，贾良玖等提出的具有鱼骨式核心单元的BRB 支撑均旨在改善变形能力[12]，但国内外学者对提高BRB 支撑延性行为的研究仍涉及较少。 特别是近年来ChiChi 地震（1999 年）[13]、汶川地震（2008 年）[14]、日本Tohoku-Oki 地震（2011 年）[15]都在震后出现了持续时间较长的强余震，这有可能导致BRB 支撑核心单元发生失稳或断裂，对于BRB 支撑的延性提出了更高要求。

本文提出了一种逐级屈服的新型延性装配式防屈曲钢支撑 （Ductile Assembled Buckling Resistant Brace，DA-BRB），所提出新型DA-BRB 支撑的设计理念是通过设置限位高强螺栓确保芯板逐级屈服，沿长度方向充分发展塑性，提高支撑变形能力。

在试验验证正确的基础上，采用ABAQUS 软件建立了新型DA-BRB 支撑的精细化有限元试件，考虑芯板楔率、芯板高厚比等参数对其滞回性能、变形能力的影响，明确了新型DA-BRB 支撑在低周往复水平荷载作用下的受力机理及破坏模式。

1 新型DA-BRB 支撑设计

1.1 支撑构造

图1 给出了新型DA-BRB 支撑的具体构造。该支撑由多级区段的楔形芯板、限位高强螺栓、约束矩形钢管、加劲肋构成。约束矩形钢管与核心单元之间设置一定间隙，确保核心单元拉伸、压缩时运行顺畅。为降低芯板与约束矩形钢管之间的摩擦，在芯板两侧设置无粘结材料，通过喷涂弹性玻璃胶实现。 加劲肋与芯板、端板焊接，约束芯板在端部的面外变形，避免芯板在两端屈曲。 楔形芯板为每隔一段距离设置凸起的挡板，通过高强螺栓与挡板的相互作用控制芯板逐级屈服，以达到芯板由中间最小截面区段逐级向两端较大截面区段过渡，期望每个区段充分发展变形，从而能够提高DA-BRB 支撑的变形及耗能能力，达到控制芯板损伤的目的。

1.2 试件设计

图2 为BRB-1 试件的几何尺寸。 为确保新型DA-BRB 支撑滞回性能数值模拟的准确性，采用ABAQUS软件对课题组所完成的BRB-1 试件进行了验证分析。 BRB-1 试件采用1:3 缩尺，其几何长度为1 800 mm。芯板宽度为70 mm，厚度为10 mm，芯板楔率为0.21。芯板两侧采用的约束矩形钢管截面为120 mm×60 mm×4 mm。采用30 颗12.9 级M12 高强螺栓将两个约束矩形钢管可靠连接。 两个约束矩形钢管之间设置垫片确保两者之间留有1 mm 缝隙。芯板两端焊接端板，端板几何尺寸为230 mm×180 mm，厚度为20 mm。 加劲肋为270 mm×55 mm，厚度为10 mm。 试件BRB-1 所采用的钢材均为Q235B 级。

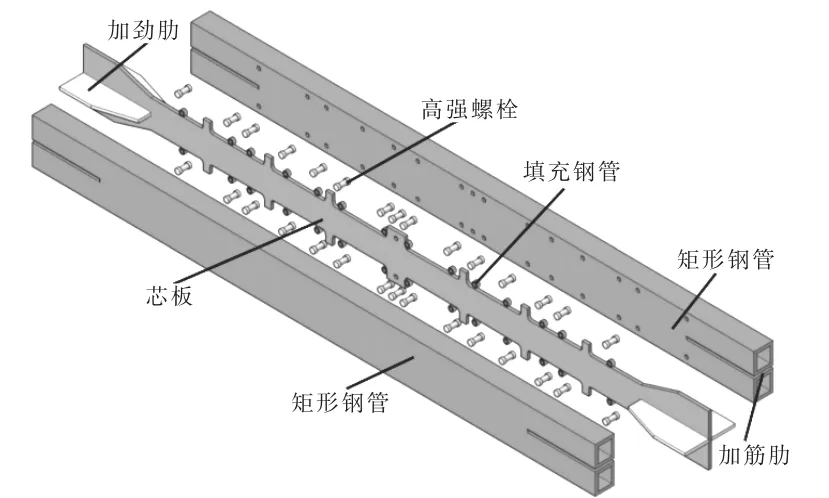
图1 新型DA-BRB 支撑的构造

图2 试件BRB-1 的几何尺寸

2 有限元验证与分析

2.1 试件BRB-1 的有限元模型及网格划分

试件BRB-1 的所有部件均采用C3D8R 减缩实体单元，螺栓与螺栓孔处均采用相同的网格划分。为精确反映芯板的力学特征，对其网格进行了加密，其他部件采用粗网格。 试件的芯板与约束钢管之间采用“面-面”接触，其他部件之间的相互作用采用通用接触，由于实际试件的芯板与约束钢管之间填充无粘结弹性玻璃胶材料，因此切向接触属性定义为无摩擦，法向定义为硬接触。为简化，高强螺栓与约束钢管采用Tie 绑定约束，高强螺栓与挡板之间采用硬接触[16]。为合理模拟芯板的初始缺陷，对支撑的芯板进行了屈曲分析，引入第1 阶屈曲模态，缺陷幅值取1‰。 试件BRB-1 的其中一端采用固定约束，另外一端施加轴向位移。 试件BRB-1 的有限元模型见图3。

图3 试件BRB-1 的有限元模型

2.2 材料性能

试件BRB-1 的核心单元采用Q235B 钢材， 矩形钢管等约束单元采用Q345B 钢材， 其应力-应变曲线采用双线性模型，并采用随动模型模拟钢材的包辛格效应。由于约束部件未进入弹塑性，表1 仅给出试件BRB-1 芯板的钢材力学性能。

表1 钢材的力学性能

2.3 加载制度

试验全程采用位移加载，沿支撑的轴向施加位移。 加载制度参考美国SAC（1997）规范[17]。 考虑到有限元模型单元数量大，计算成本高，为提高计算效率，每级荷载循环1 次，加载制度见图4。 图4 中，Δ/L 为支撑的平均轴向应变；N 为加载步。

图4 加载制度

2.4 试验验证

图5给出了试件BRB-1 的有限元模拟与试验结果的对比。由图5 可知，正向加载时，有限元模拟得到的曲线比试验稍低，主要原因是当芯板受压屈曲时，芯板与外围约束钢管之间的摩擦力会逐渐增大。 负向加载时芯板受拉，芯板与外围约束钢管之间的摩擦力减小，其有限元模拟曲线与试件基本重合。 通过在芯板上设置挡板可有效地使应力从内而外依次发散，从而控制芯板其他区段的屈服顺序，试验及有限元模拟结果均证实这种现象。 但当芯板楔率较大时，最终仍在截面最小区段形成薄弱环节，并在往复荷载作用下拉断，试件BRB-1 的有限元模拟结果也捕捉到了这种破坏模式。 总体上，有限元模拟的滞回曲线同试验结果吻合良好，破坏模式一致。 精细化有限元模型能有效评估新型DA-BRB 支撑的受力特征，进一步验证了有限元模拟方法的科学性和准确性。

图5 试件BRB-1 的有限元模拟和试验结果的对比

3 影响参数分析

3.1 试件设计

为消除尺寸效应，在进行参数有限元分析时，BASE 试件采用足尺试件，构造参图2。 BASE 试件的设计长度L=5 000 mm，芯板被划分为8 个区段，楔率为0.042。 芯板宽度为200 mm，厚度为20 mm。 采用30 颗M27 高强螺栓限位， 约束钢管的几何尺寸为350 mm×175 mm×20 mm。 芯板钢材采用Q235B 级， 弹性模量2.06×105MPa，屈服强度为235 MPa，抗拉强度为415 MPa，泊松比0.3。 约束钢管采用Q345B 级，屈服强度为345 MPa，抗拉强度为550 MPa，其他参数同Q235B 级钢材。

本文考虑了芯板类型、芯板楔率、芯板段数、芯板宽厚比4 个主要设计参数，分析了上述参数对新型DA-BRB 支撑滞回性能的影响规律。 共设计了4 组8 个试件，分析结果见下文。

3.2 芯板类型的影响

为研究芯板类型（Core Plate Type，CPT）对DA-BRB 支撑滞回性能的影响，设计了CPT 系列试件。 通过取消芯板的限位挡板，设计了普通防屈曲钢支撑试件，试件编号为BRB-CPT。

（1）CPT 系列试件的Mises 应力云图。 图6 给出了CPT 系列试件加载至平均轴向应变3.2%时芯板的Mises 应力云图。 由图6 可知，BRB-CPT 试件芯板的应力主要集中在加劲板连接端部及中间区段，BASE 试件芯板的应力从内向外依次扩展，每个区段均充分发展塑性，成功实现了新型DA-BRB 支撑的设计理念。传统防屈曲支撑已全截面屈服，必然导致在某个截面形成塑性铰断裂，由于有限元模型未能模拟芯板的颈缩破坏，导致力学行为相似。

（2）滞回曲线。图7 给出了CPT 系列试件的滞回曲线。由图7 可知， BRB-CPT 与BASE 试件的滞回曲线均稳定饱满，滞回曲线形状一致，耗能能力良好。 采用多级区段芯板对其滞回性能几乎无影响。

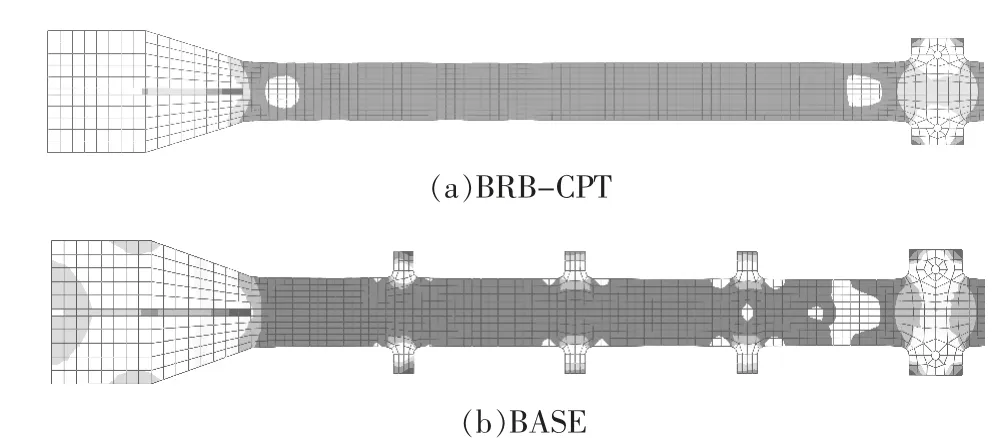
图6 CPT 系列试件的Mises 应力云图

图7 CPT 系列试件的滞回曲线

（3）骨架曲线。图8 给出了CPT 系列试件的骨架曲线。由图8 可知，随着芯板轴向位移的增加，BRB-CPT与BASE 试件的轴向承载力稳定增加，均已充分发展弹塑性，且呈理想双线性。 两个试件的骨架曲线基本重合，通过在芯板上增设挡板对此类BRB 支撑的轴向承载力影响很小。

（4）轴向刚度。轴向刚度退化曲线可真实地反映支撑在加载过程中的损伤历程，采用“点对点”刚度评价，按下式计算

式中，K 为支撑的“点对点”轴向刚度；P+、P-为同一滞回环正、负向峰值荷载Δ+、Δ-为同一滞回环正、负向峰值轴向位移。

图9 给出了CPT 系列的轴向刚度退化曲线。由图9 可知，随着平均应变的增加，BRB-CPT 与BASE 均逐渐由弹性过渡到弹塑性阶段，抗侧刚度逐渐降低，最后趋于平缓。 BRB-CPT 与BASE 轴向刚度基本相同。

（5）耗能能力。 耗能能力是评价结构或构件抗震性能的重要指标，通常采用无量纲的等效黏滞阻尼比（ξeq）指标衡量，见图10。 即

图11 给出了CPT 系列的ξeq。 由此可知， 随着轴向位移的增大，BRB-CPT 与BASE 的等效黏滞阻尼比略呈降低趋势。 BRB-CPT 与BASE 的最大等效黏滞阻尼比较大，为0.53，充分说明试件具有良好的耗能能力。 芯板上设置挡板对支撑的耗能能力几乎无影响。

3.3 芯板楔率的影响

为研究芯板楔率（Tapering Ratio of Core plate，简称TRC）对新型DA-BRB 支撑力学性能的影响， 设计了TRC 系列试件， 试件编号为TRC-1、TRC-2。 其中，试件TRC-1 的芯板楔率为0.25，试件TRC-2 的芯板楔率为0.43，其他参数同BASE 试件。

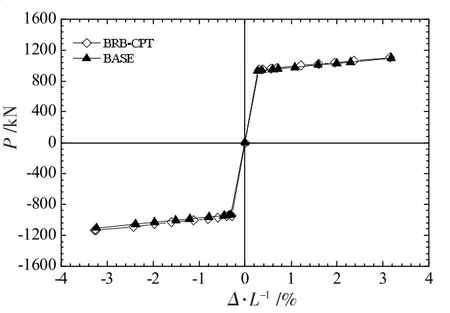
图8 CPT 系列试件的骨架曲线

图9 CPT 系列试件的轴向刚度退化曲线

图10 等效黏滞阻尼比

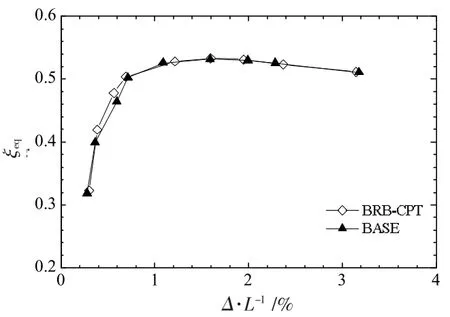
图11 CPT 系列试件的等效黏滞阻尼比

（1）TRC 系列试件的Mises 应力云图。 图12 给出了TRC 系列试件破坏时的Mises 应力云图。 由图12 可知，随着芯板楔率的增加，新型DA-BRB 支撑的破坏模式发生明显变化。当芯板楔率较小时，BASE 试件中芯板的最外侧区段破坏，其他区段可充分发展塑性变形。 当芯板楔率较大时，TRC-2 试件的破坏位置发生在内侧截面最小区段，其他区段未能充分变形。 上述分析结果充分说明通过优化芯板楔率可实现芯板区段逐级屈服。

（2）TRC 系列的滞回曲线。图13 给出了TRC 系列试件的滞回曲线。由图13 可知，芯板楔率对TRC 系列试件的滞回曲线形状影响较小，滞回曲线均呈饱满的梭形。 但随着芯板楔率的增加，由于塑性区域集中在芯板最小截面，导致滞回曲线拐点处出现圆弧形状。

图12 TRC 系列试件的Mises 应力云图

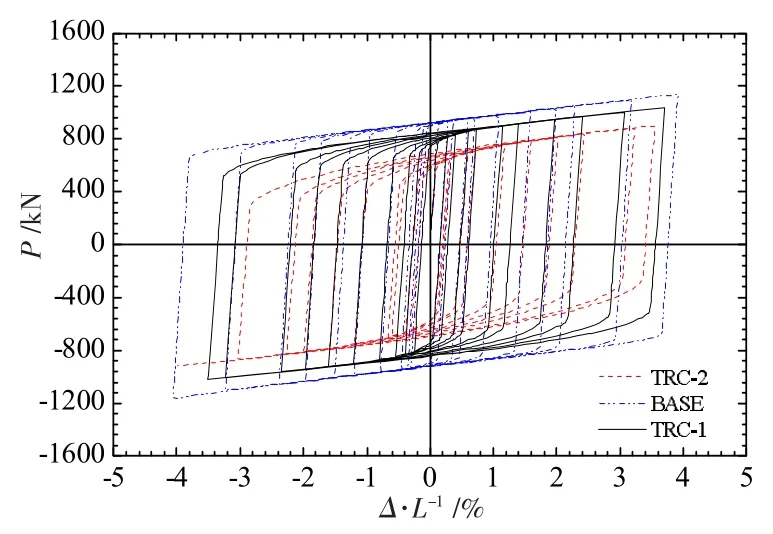
图13 TRC 系列试件的滞回曲线

（3）TRC 系列的骨架曲线。 图14 给出了TRC 系列试件的骨架曲线。 由图14 可知，改变芯板楔率变化对新型DA-BRB 支撑的轴向承载力影响较大。 随着芯板楔率的增加，新型DA-BRB 支撑的轴向承载力呈显著的降低趋势。 主要原因是随着芯板斜率的增加，在保持芯板区段数目不变的前提下，由于每个区段的横截面减小，致使轴向承载力逐渐降低。

（4）TRC 系列的轴向刚度。 图15 给出了TRC 系列的轴向刚度退化曲线。 由图15 可知，BASE、TRC-1 和TRC-2 试件的刚度退化规律较为一致。 加载初期，试件的轴向刚度退化迅速；加载后期，支撑芯板充分发展塑性， 试件的轴向刚度退化缓慢、 均匀。 BASE、TRC-1 和TRC-2 的初始轴向刚度分别为83.98、81.39 和57.07 kN/mm。 当芯板楔率从0.042 增加到0.43，支撑的初始轴向刚度降低31.22%。 随着支撑芯板楔率的增加，新型DA-BRB 支撑的轴向刚度呈降低趋势。

（5）TRC 系列的耗能能力。 图16 给出了TRC 系列试件的等效黏滞阻尼比。 由图16 可知，随着轴向位移的增加，新型DA-BRB 支撑逐渐进入弹塑性状态，其等效黏滞阻尼比呈先增加后缓慢降低的趋势。 BASE、TRC-1 试件的最大等效黏滞阻尼比均超过0.5，说明其滞回曲线均很饱满。TRC-2 试件的最大等效黏滞阻尼比降为0.47，说明随着芯板楔率的增加，新型DA-BRB 支撑的耗能能力轻微降低。

图14 TRC 系列的骨架曲线

图15 TRC 系列的轴向刚度退化曲线

图16 TRC 系列的等效黏滞阻尼比

3.4 芯板区段数的影响

为研究芯板区段数目（Number of Yield Segment，简称NYS）对新型DA-BRB 支撑力学性能的影响，设计了NYS 系列试件，试件编号为NYS-1、NYS-2；其中，试件NYS-1 的芯板区段数为6，试件NYS-2 的芯板区段数为4，其他参数同BASE 试件。

（1）NYS 系列试件的Mises 应力云图。 图17 给出了NYS 系列试件最终破坏的Mises 应力云图。 由图17可知，在芯板楔率较小的情况下，随着芯板区段数的增加，并未改变其破坏模式，NYS-1 及NYS-2 试件的破坏位置及最大应力处均发生在芯板最外侧区段，芯板挡板与高强螺栓接触，确保其他区段可充分发展变形。但芯板区段如划分过少，会导致后期变形集中在某一区段，整个芯板变形能力无法充分发挥。

（2）NYS 系列试件的滞回曲线。 图18 给出了NYS 系列试件的滞回曲线。 由图18 可知，随着芯板区段数的改变，NYS-1、NYS-2 试件与BASE 试件的滞回曲线基本重合，说明芯板区段数对新型DA-BRB 支撑滞回性能影响很小。

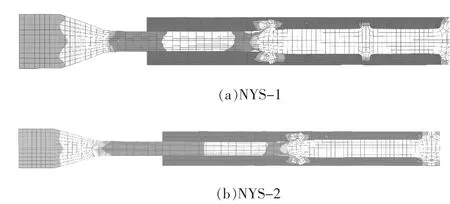
图17 NYS 系列试件的Mises 应力云图

图18 NYS 系列试件的滞回曲线

（3）NYS 系列试件的骨架曲线。 图19 给出了NYS 系列试件的骨架曲线。 由图19 可知，改变芯板区段数对新型DA-BRB 支撑的承载力影响不大。主要原因是尽管芯板区段数减少，但其芯板楔率保持不变，芯板所提供的轴向承载力基本一致。

（4）NYS 系列试件的轴向刚度。 图20 给出了NYS 系列的轴向刚度退化曲线。 由图20 可知，NYS-1、NYS-2 与BASE 试件的轴向刚度退化曲线基本重合，退化规律一致。 NYS-1、NYS-2 的初始轴向刚度分别为83.05 kN/mm、80.97 kN/mm，两者差异很小。 总体上，芯板区段数对新型DA-BRB 支撑轴向刚度影响很小。

（5）NYS 系列试件的耗能能力。 图21 给出了NYS 系列试件的等效黏滞阻尼比。 由图21 可知，NYS-1、NYS-2 试件与BASE 试件的等效黏滞阻尼比基本重合。由于芯板区段数对新型DA-BRB 支撑的滞回曲线形状影响很小，因此对其耗能能力影响也就不大。

图19 NYS 系列试件的骨架曲线

图20 NYS 系列的轴向刚度退化曲线

图21 NYS 系列的等效黏滞阻尼比

3.5 芯板宽厚比的影响

为研究芯板宽厚比（Width-to-thickness Ratio of Core Plate，WRCP）对新型DA-BRB 支撑力学性能的影响，通过改变芯板厚度，设计了WRCP 系列试件，试件编号为WRCP-1、WRCP-2。 其中，试件WRCP-1 的芯板厚度为15 mm，其宽厚比为13.33；WRCP-2 的芯板厚度为25 mm，其宽厚比为8；其他参数同BASE 试件。

（1）WRCP 系列试件的Mises 应力云图。 图22 给出了WRCP 系列最终破坏的Mises 应力云图。 由图22可知，芯板宽厚比对新型DA-BRB 支撑的Mises 应力分布及破坏模式影响很小，应力最大处及破坏位置均出现在芯板最外侧区段，其他区段可挡板已同螺栓接触，区段芯板充分发展变形。

（2）WRCP 系列试件的滞回曲线。 图23 给出了WRCP 系列试件的滞回曲线。 由图23 可知，随着芯板宽厚比的减少，新型DA-BRB 支撑的滞回曲线的包络面积趋于增加，特别是试件在进入屈服后刚度略呈增大趋势。 但总体上，改变芯板宽厚比对新型DA-BRB 支撑滞回曲线形状影响较小。

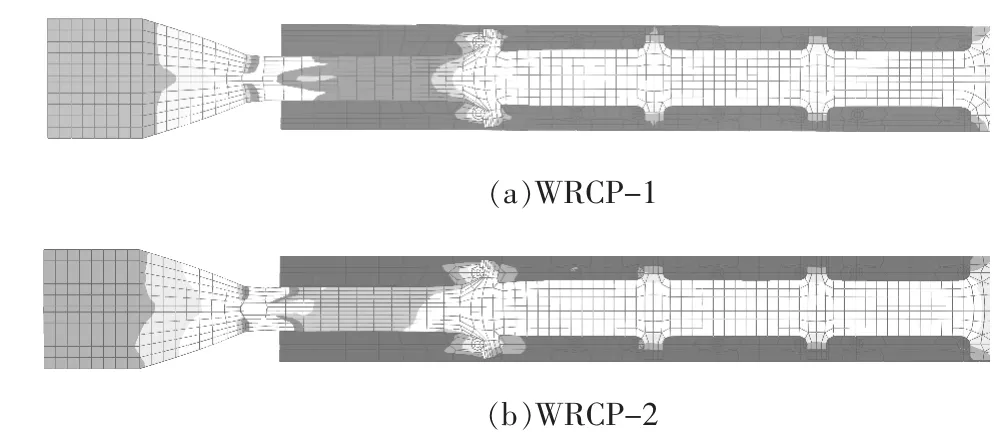
图22 WRCP 系列试件的Mises 应力云图

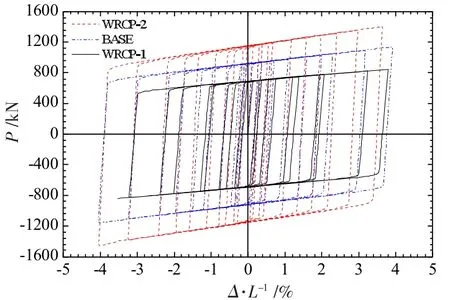
图23 WRCP 系列试件的滞回曲线

（3）WRCP 列试件的骨架曲线。图24 给出了WRCP 系列试件的骨架曲线。随着芯板宽厚比的增加，新型DA-BRB 支撑的轴向承载力呈显著的降低趋势。 在芯板轴向变形达到3.2%时， 芯板宽厚比从8 增加到13.33，试件WRCP-1 的承载力为825.6 kN，WRCP-2 的承载力为1 370.2 kN，支撑的承载力提高了66.6%。

（4）WRCP 系列试件的轴向刚度。 图25 给出了WRCP 系列试件的轴向刚度退化曲线。 改变芯板宽厚比对新型DA-BRB 支撑的初始轴向刚度影响较大，但对后期刚度退化影响较小。 WRCP-1、WRCP-2、BASE 试件的初始轴向刚度分别为63.77、104.28、83.98 kN/mm。 芯板宽厚比从13.33 降到8，支撑的初始轴向刚度提高63.5%。 在加载后期，芯板逐渐进入弹塑性阶段，WRCP 系列试件的轴向刚度均退化均匀、缓慢。

（5）WRCP 系列试件的耗能能力。 图26 给出了WRCP 系列试件的等效黏滞阻尼比。 由图26 可知，改变芯板宽厚比对新型DA-BRB 支撑的等效黏滞阻尼比基本没有影响。其主要原因是芯板宽厚比对支撑的滞回曲线形状影响很小所致。

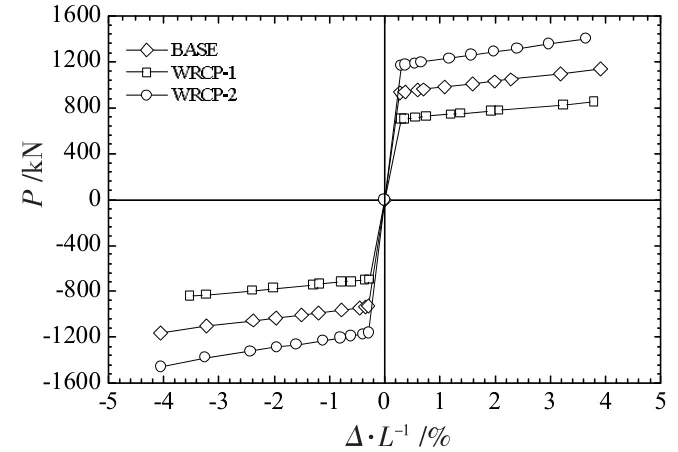
图24 WRCP 系列试件的骨架曲线

4 结论

（1）通过在新型DA-BRB 支撑的芯板上设置挡板实现逐级屈服，在获得较高轴向承载力的同时，芯板可充分发展塑性，变形能力得到提高；

（2）芯板楔率对新型DA-BRB 支撑的轴向承载力、轴向刚度、耗能能力有较大影响。 随着芯板楔率的增加，新型DA-BRB 支撑的轴向承载力、抗侧刚度、耗能能力呈降低趋势。 当芯板楔率较小时，新型DA-BRB支撑的最终破坏位置出现在最外侧区段；当芯板楔率较大时，破坏位置发生在芯板最内侧的区段；

（3）芯板区段数对新型DA-BRB 支撑的轴向承载力、轴向刚度、耗能能力的影响很小，但芯板区段数较大时，会导致芯板的有效屈服段长度降低，整体变形能力降低；

（4）在芯板宽度不变的前提下，改变芯板宽厚比对新型DA-BRB 支撑的滞回性能、耗能能力影响很小，但对轴向承载力及轴向刚度影响较大。随着芯板宽厚比的增加，新型DA-BRB 支撑的轴向承载力、初始轴向刚度呈降低趋势。