基于经验模态分解的汽车销量预测方法研究

谢鑫鑫， 朱从坤

（苏州科技大学 土木工程学院，江苏 苏州215011）

在社会倡导绿色出行，国内公共交通系统不断完善的背景下，基本型乘用汽车销量目前呈现慢增长趋势。 同时，基本型乘用型汽车销售量受宏观经济环境、消费政策、消费者收入水平等因素的影响较大，具有非线性和波动大的特点，这就要求汽车生产企业能较精准地预测未来汽车销量，从而为企业的材料采购、生产和营销策略等的决策提供指导依据[1]。 时间序列是指将某一个统计指标或现象在不同时间上的各个数值，按时间先后顺序排列而形成的序列[2]。 由于国内基本型乘用汽车销量月度数据呈现的明显非线性、非平稳性，其可以看作为以月份为刻度，当月销量为统计值的时间序列。 因此研究汽车销量月度数据形成的时间序列，并且建立时间序列预测模型，可以预测未来基本型乘用型汽车销售量。

预测时间序列的算法模型大体可分为线性回归模型、神经网络模型、支持向量机模型和自回归差分移动平均模型等等[3]。 线性回归模型可以对波动较平稳且有规律的时间序列进行很好的预测，但当时间粒度较小，或者历史数据具有较大波动性时，预测精度会大大降低，因此该模型适用于序列波动情况小，预测时间粒度较大的研究对象；神经网络算法预测精度高，但容易陷入局部最优值，且稳定性差，收敛速度水平较低，网络泛化能力较弱，需要收集大量类型数据来标定输入层和各隐藏层的参数，应用复杂；支持向量机性能受核函数影响大，且参数选取具有一定随意性，建模计算复杂，不利于在生产实际中的运用普及；自回归差分移动平均模型（ARIMA）对于波动性较小的且有规律的时间序列具有较高的预测精度，且应用方法简单，无需大量参数标定，适用于普遍类型的时间序列预测中[4-6]。 汽车销量月度数据呈现明显非线性、非平稳性特点，所以若将该复杂时间序列分解为若干平稳时间序列，而后运用ARIMA 方法预测平稳时间序列，则可使得汽车销量预测方法变得简便易使用。

本研究引入经验模态分解（Empirical Mode Decomposition，EMD），将复杂时间序列分解为若干平稳时间序列。 经验模态分解最早是N. E. Huang 等于1998 年提出的一种处理分析非线性、非平稳复杂信号的方法，即将复杂信号分解为若干平稳序列[7]。 自EMD 提出以来，已广泛应用于故障分析、地球物理学、结构分析等领域[8-9]。 目前也有越来越多的学者将EMD 与其他预测算法结合，将原始的复杂序列平稳化，以适应不同预测对象，提高预测精度。 刘慧婷等将EMD 与多层反馈神经网络相结合，将股票价格波动时间序列平稳化，从而应用于股票预测中的模拟匹配[10]；Xun Zhang 等将EEMD 分别与FNN 和SVM 相结合，预测石油价格复杂变化，预测效果良好[11]；任国成等同样运用EMD 方法将非线性的电力负荷时间序列平稳化，并结合LSTM 算法预测短期电力负荷[12]；李栋和李晓龙则以EMD 法组合其他预测模型，分别预测了地区降水量和航空客流量，预测精度较好[13-14]。 综上所述，可将非线性、非平稳性的时间序列通过经验模态分解后可得到若干较平稳序列，而后结合其他预测算法对平稳序列进行预测，探求预测效果。

因此本文将运用经验模态分解（EMD）法对汽车月度销量时间序列进行平稳化分解。 首先通过对销量月度历史时间序列进行经验模态分解，得到若干平稳本征模函数IMFn和一个残差趋势项R；其次将各分量重组为高、低频序列和趋势项序列，分别运用ARIMA 预测；而后将各分量预测结果汇总为最终预测数据，并与实际值对比。

1 经验模态分解（EMD）

经验模态分解（EMD）是对数据时间序列或信号序列的平稳化处理，仅仅依据数据自身的时间尺度特征进行原始信号的分解，把复杂信号分解成若干个本征模态函数IMF 以及一个残差趋势项R。 各分解出的本征模函数较原始信号变得相对平稳，且包含了原信号不同的尺度特征；残差趋势项平缓，表达了原信号的总体变化趋势。 EMD 分解基本方法如下：

步骤（1）设原始信号序列为x（t），找出序列中所有极大值点和极小值点，并用三次样条插值法分别拟合成原序列的上包络线μ+（t）和下包络线μ-（t），并取两者均值为m1（t），公式如下

步骤（2）将均值m1（t）从原始序列x（t）中减去，得到新的序列f1（t），公式如下

若f1（t）不满足本征模函数的确认要求，则将f1（t）作为新的原始序列x1（t），重复上述步骤（1）和（2），直至得到的某个fk（t）满足预设的本征模函数要求。 满足本征模函数要求的两个条件为：该函数fk（t）的极值点数目和过零点数目至多相差1；由局部极大值点和局部极小值点构成的两条包络线平均值趋近于零。

步骤（3）令得到的第一个满足本征模函数要求的fk（t）记为IMF1，将IMF1从原始序列x（t）中扣除得到新的序列r1（t），作为新的信号序列，重复步骤（1）和（2），直至得到的某个rn（t）为单调函数或简单的趋势曲线，将其作为残差趋势序列R。 最终，原始序列可以表达为若干个IMF 分量和一个残差趋势序列rn（t），即

2 基于EMD 的汽车销量预测

2.1 数据描述

本文涉及的国内基本型乘用汽车（轿车）的当期销售量月度数据来源于中经网统计数据库。2000 年1 月至2019 年12 月，共240 个月当期销量为研究样本，如图1 中原始序列所示。 其中以2000 年1 月至2019 年6 月共234 个月的月度销量数据为训练样本，以2019 年7 月至2019 年12 月共6 个月的月度销量数据为测试样本，用于评价本文预测方法的准确性。

图1 销量原始序列与残差序列曲线

2.2 EMD 分解

利用经验模态分解方法对前234 个汽车销量月度数据进行处理，从而得到原始序列中不同时间尺度上的变化特征。 基于MATLAB 平台，分解原始序列后，得到6 个IMF 分量以及1 个残差趋势项R。 如图1 和图2 所示，各IMF 分量波动频率依次逐渐减小，较原始序列明显平稳，残差趋势项R 表达了原始序列的总体趋势。

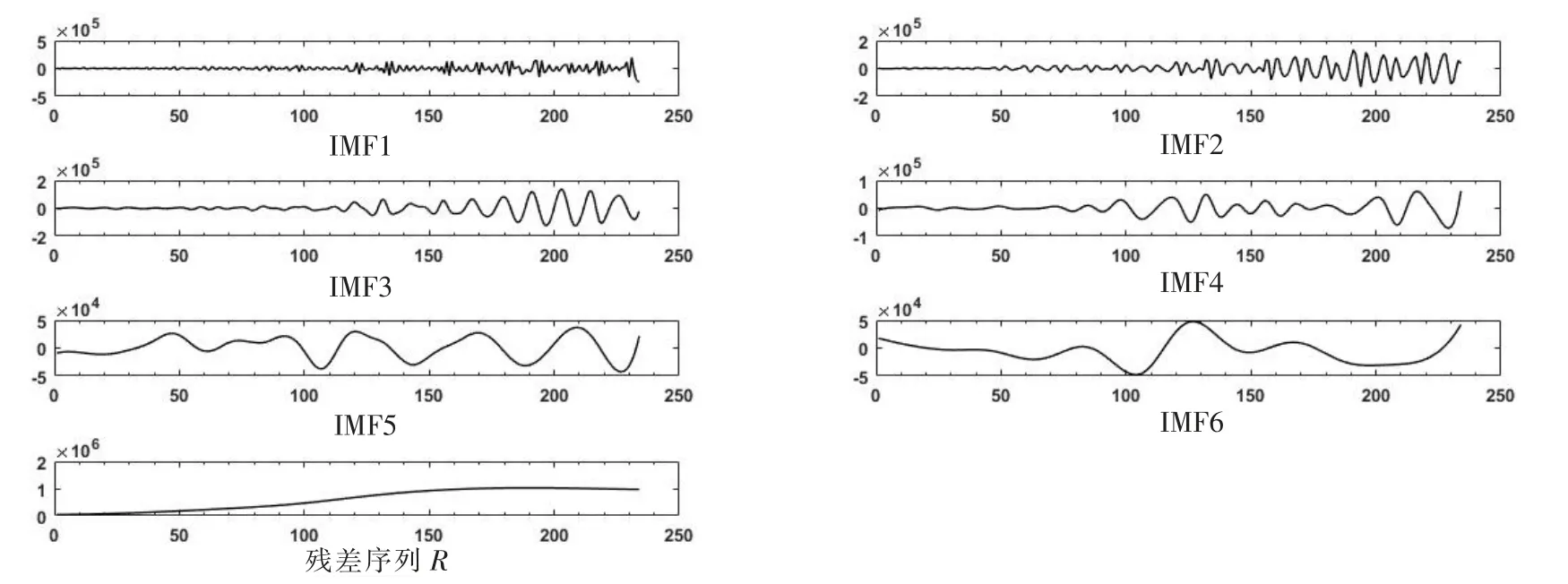
图2 EMD 分解结果

2.3 IMF 分量与残差序列R 相关统计描述

表1 给出了各IMF 分量和残差序列R 与原始序列的皮尔森相关系数、肯德尔和谐系数以及方差。 皮尔森相关系数π 是用来反应两个变量线性相关强弱程度的统计量，π 可由（Xi，Yi） 样本点的标准分数均值估计，其值介于-1 到1 之间，绝对值越大表明相关性越强，计算方法如式（4）所示[16]。 肯达尔和谐系数是计算多个等级变量相关程度的一种方法[17]，肯德尔和谐系数的取值范围在-1 到1 之间，当W 为1 时，表示两个随机变量拥有一致的等级相关性；当W 为-1 时，表示两个随机变量拥有完全相反的等级相关性；当W 为0 时，表示两个随机变量是相互独立的，肯德尔和谐系数W 计算方法如式（5）所示。

式中，NCP（number of concordant pairs）为和谐观察值对，NDCP（number of disconcordant pairs）为非和谐观察值对。 序列X、Y，其元素个数均为n，两个序列取的第i（1≤i≤n）个值分别用Xi、Yi表示，若Xi＞Xj且Yi＞Yj（或Xi＜Xj且Yi＜Yj），则为和谐观察值对，其余情况为非和谐观察值对。

由表1 可知，残差序列R 的皮尔森相关系数和肯德尔和谐系数分别为0.963 和0.796，可见残差序列与原始序列相关性最大，表达了原始序列的主要趋势特征；分量IMF1～IMF3的相关系数总体大于IMF4～IMF6，但都远小于残差序列的相关系数，即各分量表达了原始序列的次要特征。

方差大小反应了序列的波动情况， 即变量偏离期望值的程度， 残差序列方差占比原始序列方差为95.69%，反应了原始序列的总体波动情况；IMF1～IMF6分量的方差贡献率较小，表现为原始序列曲线在残差趋势曲线附近震荡，如图1 所示。 由于在筛选本征模函数IMF 时，应用了三次样条插值法分别拟合原序列的上包络线和下包络线， 因此， 导致筛选出的残差序列R 与IMF1～IMF6的方差占原始序列方差之比的和为101.64%，略大于100%，是经验模态分解结果产生的不可避免的误差。

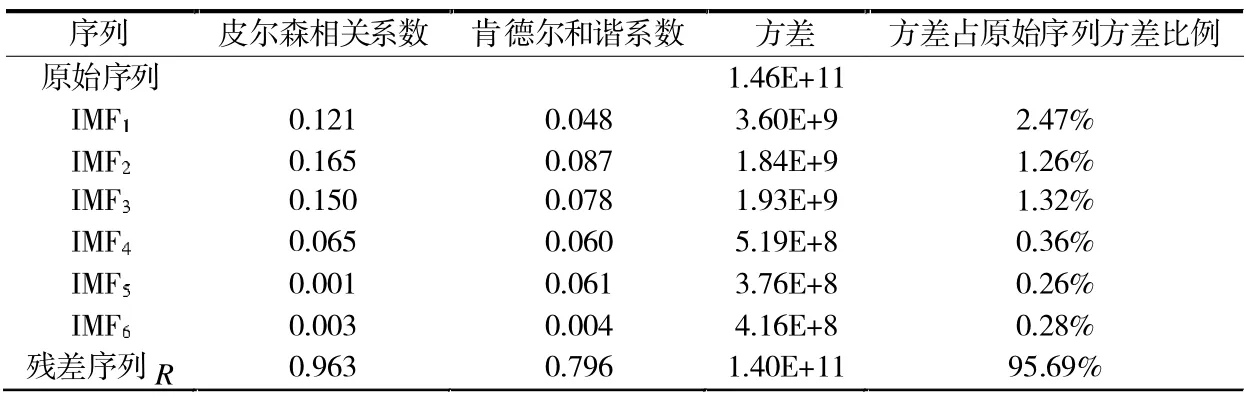
表1 各分量相关统计结果

2.4 IMFn 分组

原始序列通过经验模态分解后，得到6 个本征模函数和1 个残差序列趋势项。 首先，分解出本征模函数时，采用的三次样条插值法和终止条件，会使得重构成的原始序列与实际原始序列之间存在一定分解误差；其次，若每个IMF 分量，运用相关预测模型预测，然后将各分量的预测结果累加为最终预测结果，则会放大误差。 因此应通过对各本征模函数合理分组，形成高频序列、低频序列和趋势序列后，再分别运用相关模型预测，可降低累积误差。

通过对表1 的相关系数和方差占比的分析，以IMF1～IMF3累加得高频序列，IMF4～IMF6累加得低频序列，残差序列R 为趋势序列。 表2 为高、低频序列和趋势项序列的各相关系数以及方差占比情况，可见高频序列在皮尔森相关系数、肯德尔和谐系数比原有各分量明显提高，表明重组后的高频序列较分量IMF1～IMF3与原始序列有更高的相关性。 低频序列的皮尔森相关系数、肯德尔和谐系数较原有各分量无明显提高，表示重组后的低频序列反映了与原始序列较弱的相关性。

表2 高、低频序列及趋势项序列相关统计结果

2.5 预测结果

将原始序列EMD 分解后的本征模函数进行高、低频序列和趋势项序列分组后，基于SPSS 平台，采用差分自回归移动平均模型（ARIMA）预测。 对于高频序列，其偏自相关系数1 阶截尾，自相关系数4 阶截尾，季节性一阶差分序列自相关系1 阶截尾，可以建立ARIMA（1,0,4）（0,1,1）模型；对于低频序列，其三阶差分序列偏自相关系数4 阶截尾， 季节性一阶差分序列偏自相关系数和自相关系数均1 阶截尾， 可以建立ARIMA（4,3,0）（1,1,1）模型；对于残差趋势项R，其四阶差分序列偏自相关系数1 阶截尾，可以建立ARIMA（1,4,0）模型。

预测结果如图3 所示和表3 所列，曲线EMD-ARIMA 为将高、低频序列以及趋势项序列预测结果累加得到最终预测结果； 曲线ARIMA 为原始数据直接运用ARIMA 预测的结果； 曲线EMD-D-ARIMA 为将各IMF 分量与趋势项序列分别运用ARIMA 预测的最终累加预测结果。

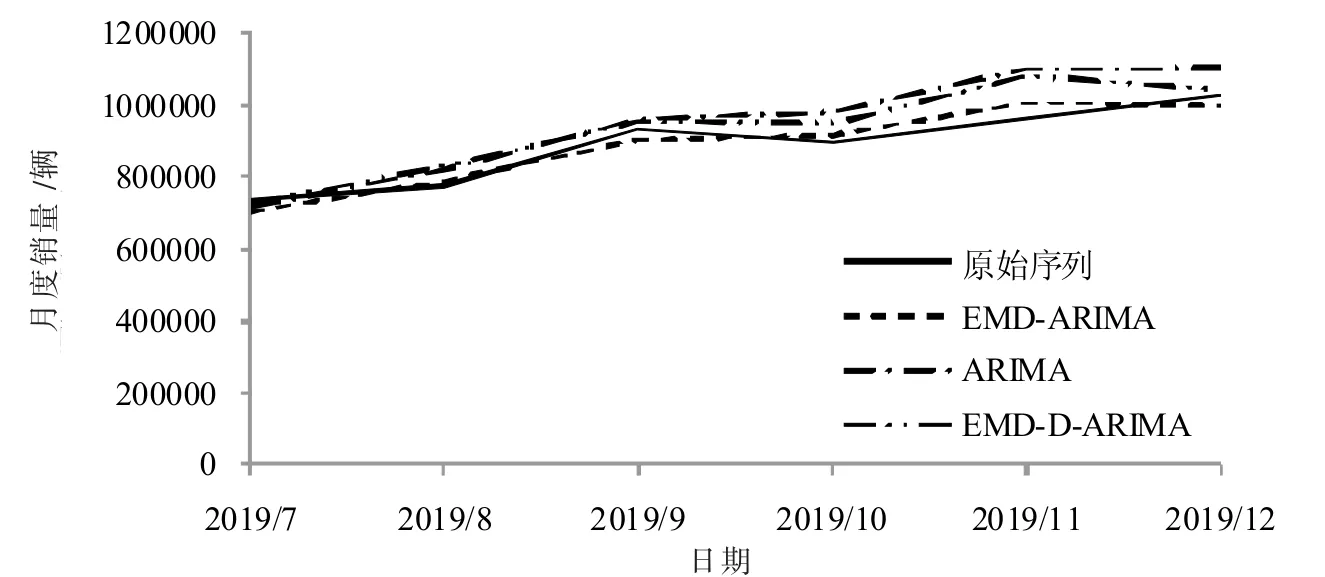
图3 预测结果曲线

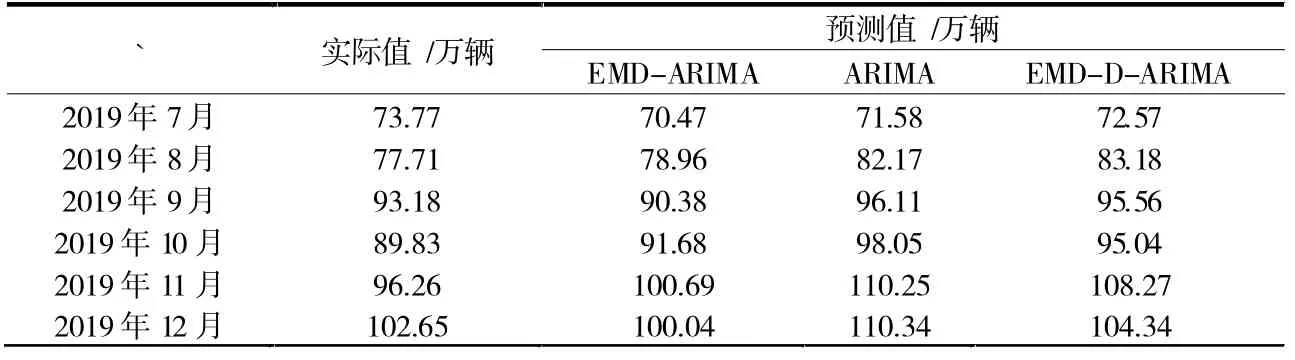
表3 预测结果

3 预测精度

本文利用平均绝对百分比误差（MAPE）、平均绝对误差（MAD）和均方根误差（MSE）评价预测精度，其计算公式分别如下[18]

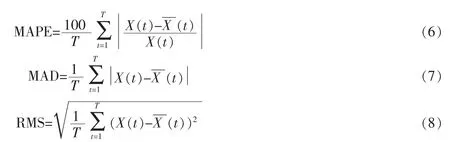
EMD-ARIMA、ARIMA 和EMD-D-ARIMA 三种方法的预测误差见表4。EMD-ARIMA 组合算法，在预测结果误差分析中，其平均绝对百分比误差（MAPE）、平均绝对误差（MAD）和均方误差（MSE）均最小，即相比较于直接运用ARIMA 方法预测和EMD-D-ARIMA，在基本型乘用汽车的月度销量预测中EMD-ARIMA 组合算法预测效果更有优势。

表4 预测误差

由于ARIMA 在预测平稳序列时的精度较好，而原始汽车月度数据呈现非平稳的特点，因此运用经验模态分解原始数据并重组后，原始数据被分解为相对平稳的高、低频序列和残差序列，再运用ARIMA 模型预测效果会更好。 因为EMD 分解本身就不可避免存在误差，若直接将EMD 分解后的IMF 分量和趋势项R 分别运用ARIMA 预测并累加，则会导致预测误差堆积，即EMD-D-ARIMA 预测算法较EMD-ARIMA 预测算法存在更大的误差堆积。

4 结语

本文运用经验模态分解方法，将国内基本型乘用汽车的月度销售量时间序列进行分解，得到6 个本征模函数和1 个残差序列趋势项，而后将各分量重组为高、低频序列和一个趋势项，并通过差分自回归移动平均模型ARIMA 进行2019 年7 月至2019 年12 月的月度销量预测， 相比直接运用ARIMA 和EMD-D-ARIMA预测，EMD-ARIMA 预测效果更好。在今后的研究中，可以考虑针对不同时间序列研究对象的特点，如预测时间粒度和序列平稳性等等，运用其他合适预测算法与经验模态分解EMD 进行组合预测，探究经验模态分解方法在时间序列预测中的合理性和适用性。