三阶屈服屈曲约束支撑耗能机理及设计方法研究

胡宝琳，徐世安，徐 庆，吴仁杰

(上海大学力学与工程科学学院土木工程系，上海 200444)

传统的抗震设计主要致力于提升建筑结构本身的抗震性能来抵御地震作用，即“硬碰硬”硬抗。随着对地震作用研究的深入，研究人员意识到，地震作用于结构而言本质上是一种能量输入的体现。因此，消能减震技术步入大众视野。屈曲约束支撑(BRB)在受拉压荷载作用时都进入全截面屈服，抗震性能优越，且构造简单易加工，在工程中得到大量应用[1−4]，国内外学者也对其进行了广泛的研究[5− 6]。

KIMURA 等[7]将普通支撑放入装有水泥砂浆的钢套筒中，提出了能耗散地震能量但不会屈曲的支撑，并进行试验研究，得到了稳定而饱满的滞回曲线。FUJIMOTO 等[8]以砂浆作为填充料，并改变钢套筒的尺寸，进行了试验研究，得到了核心单元与钢套筒设计关系，提出了钢套筒的设计准则。郭彦林等[9]针对一种四角钢组合约束型防屈曲支撑构件，给出单向受弯时的外围螺栓内力的计算方法。胡宝琳等[10]针对罕遇地震荷载作用下的屈曲约束支撑框架结构，从附加有效阻尼比的角度出发，通过理论分析给出了屈曲约束支撑框架结构体系弹塑性位移的简化求解方法。李国强等[11]根据屈曲约束支撑滞回特征提出了一种滞回模型，并建立了其弹塑性刚度方程，通过试验对比得出该模型能够准确地反映屈曲约束支撑在承受反复荷载时的滞回特点。徐龙河等[12]提出一种新型自复位全钢型防屈曲支撑，对其基本构造和工作原理进行了介绍，建立了能够准确描述支撑滞回特性的恢复力模型。曾聪等[13]提出了一种全钢装配式防屈曲支撑，并通过拟静力试验，研究了其滞回性能、抗震性能及破坏机理。胡宝琳等[14]提出了一种“类十字”双阶屈服屈曲约束支撑，并结合理论和模拟对支撑的工作原理和力学性能进行了研究。LI 等[15]提出了一种由传统BRB 和金属剪切阻尼器复合的新型二阶屈服支撑，建立了其力学模型，并通过试验验证了该支撑的可行性。BARBAGALLO 等[16]提出将双阶屈曲约束支撑运用于钢框架结构，并给出了双阶屈曲约束支撑钢框架的设计方法。

传统屈曲约束支撑在较小地震作用下保持弹性，仅在较大地震时屈服耗能，且支撑屈服点单一仅能在对应的地震条件下发挥作用，无法满足不同强度地震作用的使用需求。因此，本文提出一种能够三阶屈服的屈曲约束支撑(Triple yield buckling restrained brace, 简称TYBRB)，其在小震下可以实现第一阶、第二阶屈服，在大震下进入第三阶屈服，能够满足不同强度地震作用的使用需求，耗能性能更加优越。首先对其构造组成及工作机理进行研究，在力学分析的基础上，建立了TYBRB 支撑的刚度方程、各阶屈服力和屈服位移的计算方法。并通过数值模拟研究TYBRB 设计的合理性，对TYBRB 的抗震性能进行综合分析。

1 三阶屈服支撑介绍

1.1 构造设计

三阶屈服屈曲约束支撑由内核单元和外围约束部件等组成，如图1 所示。内核单元可分为五块核心板，包括一块F 芯板、两块R 芯板、两块Y 芯板，如图2 所示。五块核心板通过两端的L1连接段连接为一个整体；三阶屈服屈曲约束支撑R 芯板、Y 芯板及F 芯板仅在两端L1连接段连接，中间屈服段及非屈服段不连接，且Y 芯板与F 芯板采用两种不同屈服点的钢材。五块核心板组成三阶屈曲约束支撑核心单元共同承受荷载，外围约束部件抑制核心单元平面外变形，防止核心单元受压发生屈曲，两者之间设有缝隙和隔离材料以降低相互作用及材料泊松比的影响。

图1 TYBRB 整体示意图Fig.1 Overall diagram of TYBRB

图2 核心单元整体及分解示意图Fig.2 Overall and disassemble diagram of core plate

为使R 芯板、Y 芯板非屈服段不发生屈服，可通过增大非屈服段的截面尺寸或焊加劲肋来增大非屈服段受力面积，使其与屈服段的面积比大于钢材的强屈比，从而达到屈服段屈服时非屈服段仍处于弹性阶段的目的。

1.2 工作原理

当屈曲约束支撑套筒具有足够大的刚度，足以约束内核单元不发生屈曲，此时可建立三阶屈曲约束支撑的简化力学模型(如图3 所示)。

图3 TYBRB 核心单元力学模型Fig.3 Mechanical model of core plate of TYBRB

如图3 所示，三阶屈曲约束支撑是通过控制R 芯板(L3段)、Y 芯板(L5段)和F 芯板(L6段)的刚度比，进而达到控制各屈服段的应力大小，并结合芯板采用不同屈服点钢材，即R 芯板、Y 芯板采用同种屈服点的钢材，F 芯板采用相对较大屈服点钢材，来实现支撑三阶屈服耗能。

对于R 芯板与Y 芯板非连接段，在两个芯板非连接段的非屈服段和屈服段截面积相同的情况下，即A2=A4，A3=A5，当非屈服段长度L2>L4，则KRe>KYe，又因F=K∆ 、∆Rf=∆Yf(f 表示芯板非连接段)，所以FR>FY，即 σ3>σ5。因此，R 芯板与Y 芯板能先后进入屈服。对于Y 芯板与F 芯板非连接段，根据两者变形协调关系，在受轴向荷载情况下，Y 芯板和F 芯板非连接段具有同等变形，即 ∆Yf=∆Ff，且两者长度相同，根据ε=∆/L可 知，εYf=εFf。对于Y 芯板非连接段，其非屈服段截面积大于屈服段截面积，即A4>A5，根据 ∆=FL/EA、ε=∆/L可推出 ε=F/EA，所以ε5>εRf>ε4；对于F 芯板非连接段，其截面近似保持不变，所以 ε6=εFf。因此，ε5>ε6，又由胡克定律公式 σ=Eε ，所以 σ5>σ6，即能实现了Y 和F 两个芯板先后进入屈服。因此，本构造可实现三阶屈服效果，在轴向荷载的作用下R 芯板、Y 芯板、F 芯板能够依次进入屈服。

图4 是R 芯板、Y 芯板和F 芯板与TYBRB的力与位移关系曲线。可见TYBRB 的力与位移曲线等效于三种芯板相互叠加的结果，当位移分别达到R 芯板、Y 芯板、F 芯板的屈服位移时，TYBRB 也实现了相应的屈服，即实现了三阶屈服效果。叠加后的结果不仅能使支撑实现三阶段屈服，而且承载能力大幅提升。

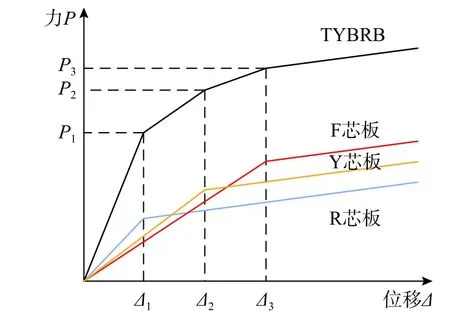
图4 TYBRB 力与位移曲线Fig.4 Force and displacement curve of TYBRB

在小震作用下，R 芯板和Y 芯板在较小变形下就实现屈服，为结构提供耗能；而F 芯板仍处于弹性状态，为结构提供侧向刚度。较大震作用下，R 芯板、Y 芯板、F 芯板均进入屈服状态，共同为结构耗能。因此，TYBRB 在较小震作用情况下可以达到承载与耗能双功能的效果，较大震作用时可以提供更多的阻尼为结构耗散能量，不仅克服了传统屈曲约束支撑小震无法耗能的缺点，且达到了不同强度地震作用分阶段屈服耗能的目的。

2 理论分析

根据第1 节中工作原理分析，定性说明了三阶屈曲约束支撑可以实现核心单元的R 芯板、Y 芯板、F 芯板依次屈服，即实现三阶屈服。本节定量分析三阶屈曲约束支撑的性能指标，具体对其各阶段刚度、屈服力以及屈服位移进行分析，并给出三阶屈曲约束支撑的简化设计方法。

2.1 刚度分析

三阶屈曲约束支撑的刚度发展分为4 个阶段：第1 阶段，R 芯板、Y 芯板和F 芯板屈服段均保持弹性；第2 阶段，R 芯板屈服段进入屈服，而Y 芯板、F 芯板屈服段仍保持弹性；第3 阶段，R 芯板、Y 芯板屈服段进入屈服，而F 芯板屈服段仍保持弹性；第4 阶段，R 芯板、Y 芯板和F 芯板屈服段均进入屈服。

根据三阶屈曲约束支撑核心单元工作原理可得到其刚度计算模型，如图5 所示。首先计算出各芯板连接段和非连接段在不同阶段的刚度，再通过叠加原理，即可得到不同阶段TYBRB 的轴向刚度。

图5 TYBRB 刚度计算模型Fig.5 Stiffness calculation model of TYBRB

1) 第1 阶段。三阶屈曲约束支撑的轴向刚度等效于非连接段并联，再与两端连接段串联。根据刚度叠加原理得三阶屈曲约束支撑的轴向刚度KS：

2) 第2 阶段。R 芯板屈服时，此阶段三阶屈曲约束支撑轴向刚度KP1：

3) 第3 阶段。Y 芯板屈服时，此阶段三阶屈曲约束支撑轴向刚度KP2：

式中，KYp为Y 芯板非连接段(L4段和L5段)屈服后刚度，

4) 第4 阶段。F 芯板屈服时，同理，此阶段三阶屈曲约束支撑轴向刚度KP3：

式中，KFp为F 芯板非连接段(L6段)屈服后刚度，KFp=αEA6/L6。

2.2 屈服承载力和位移分析

三阶屈曲约束支撑的屈服承载力和屈服位移按3 个阶段分析，分别对应于TYBRB 中R 芯板、Y 芯板、F 芯板屈服时的阶段。

1) 第1 阶段。当R 芯板进入屈服，此时Y 芯板和F 芯板尚未进入屈服仍保持为弹性，支撑的承载力为各芯板轴向力的叠加，则三阶屈曲约束支撑一阶屈服力P1为：

式中：FR1为R 芯板轴向受力，FR1=f1yA3；FY1为Y 芯板轴向受力，FY1=FR1·KYe/KRe；FF1为F芯板轴向受力，FF1=FR1·KFe/KRe；其中f1y为R 芯板屈服段屈服强度。

结合材料力学[17]公式 ∆=FL/EA，可推导出一阶屈服位移计算公式：

2) 第2 阶段。Y 芯板屈服时，三阶屈服支撑二阶屈服力P2为：

式中：FR2为R 芯板轴向受力，此阶段R 芯板进入塑性，在第1 阶段～第2 阶段过程中，dF=Kd∆，且d∆R2=d∆Y2，积 分 可 得FR2=(FY2−FY1)·KRp/KYe+FR1；FY2为Y 芯 板 轴 向 受 力，FY2=f1yA5；FF2为F 芯板轴向受力，FF2=FY2·KFe/KYe。

与 ∆1计算方法类似，可推导出二阶屈服位移：

3) 第3 阶段。则F 芯板屈服时，三阶屈服支撑三阶屈服力为：

式中：FF3为F 芯板轴向受力，FF3=f2yA6；FR3为R 芯板轴向受力，与FR2求法类似，FR3=(FF3−FF1)·KRp/KFe+FR1；FY3为Y 芯板轴向受力，FY3=(FF3−FF2)·KYp/KFe+FY2；其 中f2y为F 芯 板屈服段屈服强度。

同理，可推导出三阶屈服位移：

通过2.1 节和2.2 节对三阶支撑刚度、屈服位移和屈服力的分析，绘制三阶支撑在荷载作用下的骨架曲线(如图6 所示)。由图6 可知，TYBRB弹性阶段与卸载阶段支撑的刚度相同，期间不同芯板屈服后刚度都发生了变化，使三阶支撑在不同的阶段表现出不同的刚度特征。

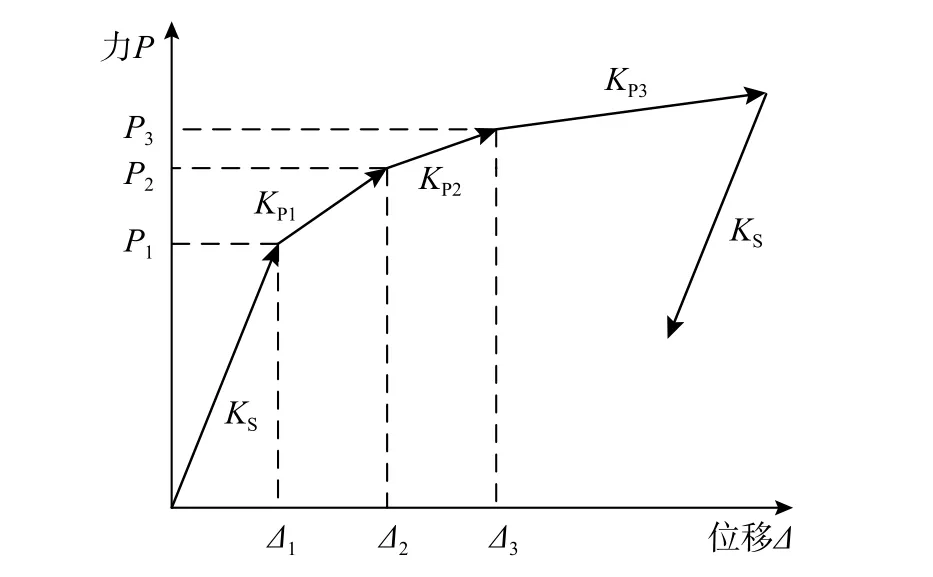
图6 TYBRB 力与位移骨架曲线Fig.6 Force and displacement skeleton curve of TYBRB

2.3 简化设计方法

TYBRB 三阶屈服性能主要受R 芯板、Y 芯板和F 芯板非连接段控制，因此不考虑两端连接段L1的影响，取非连接段单独分析，并建立TYBRB简化力学模型，如图7 所示。

图7 TYBRB 简化力学模型Fig.7 Simplified mechanical model of TYBRB

将2.2 节中的式(6)、式(8)、式(10)进行简化，可得简化的三阶位移公式：

由式(11)～式(13)可知，一阶、二阶屈服位移主要由芯板非屈服段和屈服段的长度与面积决定；三阶屈服位移主要由F 芯板材料的屈服应变、屈服段长度决定。且由1.2 节工作原理分析可知三阶屈服承载力主要由芯板的屈服段面积决定。

采用第1 节和第2 节设计方法对三阶屈服屈曲约束支撑进行设计，R 芯板、Y 芯板分别选取合适的非屈服段与屈服段长度及截面积，且Y 芯板和F 芯板采用不同屈服点钢材，可控制支撑在小变形下实现一阶、二阶屈服及合理的屈服点；合理选取R 芯板、Y 芯板、F 芯板截面积，可得到合理的各阶屈服承载力。根据支撑承载力需求合理选取以上设计参数，即可设计出满足需求的三阶屈服屈曲约束支撑。

3 有限元建模及验证

为了证明本文提出的三阶屈服屈曲约束支撑的可行性以及上述理论结果的准确性，根据理论结果设计支撑参数，利用ABAQUS 软件建立TYBRB分析模型，研究支撑的各项力学性能。

3.1 建模过程

采用ABAQUS 软件建立TYBRB 分析模型，单元类型为C3D8R 实体单元。模型有限元网格划分情况如图8 所示，TYBRB 核心单元网格大小取20 mm，约束套筒网格大小取50 mm，为了提升分析结果精度，对厚度方向网格数量进行加密。钢材的本构关系采用双折线模型，弹性模量E取值为206 GPa，强化阶段斜率取0.02E，泊松比取0.3。

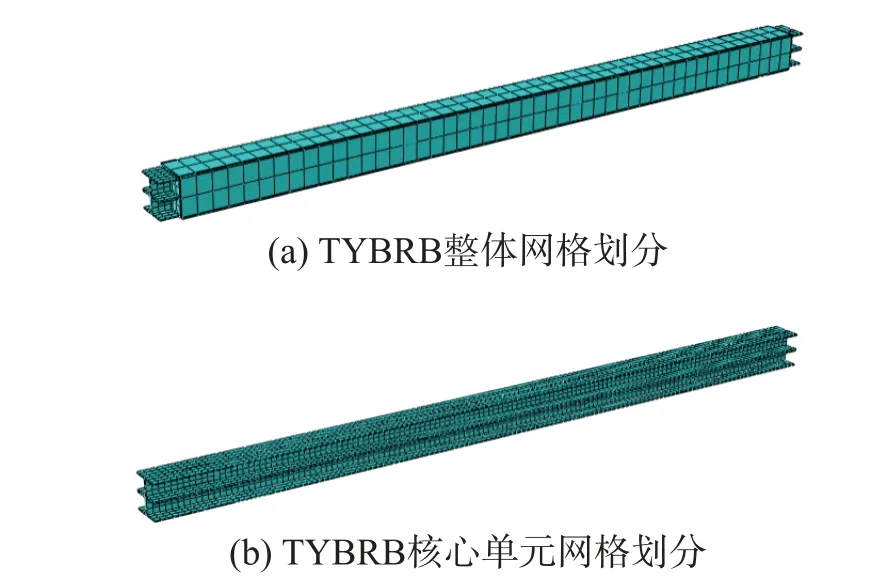
图8 TYBRB 网格划分Fig.8 Mesh schemes of TYBRB

考虑核心单元与约束套筒之间的接触，接触面法向作用采用“硬”接触；切向作用与接触压力成正比，比例系数取0.01。

为防止加载区域出现应力集中现象对结果造成影响，对加载区域进行点面耦合，并施加位移荷载。支撑两端边界条件采用铰接，在初始分析步中，约束核心单元两端3 个方向的平动自由度，进入加载分析步，将加载端的轴向自由度释放，并采用轴向位移控制进行加载；外套筒约束一端的3 个平动自由度和3 个转动自由度，不允许其沿轴向方向移动，使其仅起到抑制核心单元平面外变形的作用。加载方式采用位移加载，为了更好体现TYBRB 多阶屈服的效果，前3 级加载幅值为 ∆1y(一阶屈服位移)、∆2y(二阶屈服位移)和∆3y(三阶屈服位移)，第4 级、第5 级加载幅值为支撑长度L的1/600 和1/400，每个幅值分别循环3 次。

3.2 模型验证

为了验证本文建模方法的准确性，进行试验与模拟结果对比验证，采用文献[18]中的支撑试验数据来校验本文的建模方法。该试验件全长4176 mm，芯板长度2800 mm，A 芯板焊接段截面尺寸100 mm×32 mm，屈服段截面尺寸100 mm×16 mm，屈服段长度800 mm，B 芯板焊接段截面尺寸200 mm×32 mm，屈服段截面尺寸200 mm×16 mm，屈服段长度2000 mm，外套筒长度3360 mm，截面尺寸400 mm×300 mm×8 mm，材料均为Q235。采用位移加载，第1 循环、第2 循环加载幅值为∆1y(一阶屈服位移)、∆2y(二阶屈服位移)，第3 循环～第6 循环加载幅值采用支撑长度L的1/300、1/200、1/150、1/100，每个幅值分别循环3 次。采用本文建模方法对该试件进行建模，其有限元结果与试验结果比较如图9 所示。

图9 有限元结果与试验结果对比Fig.9 Comparison between test and finite element results

由图9 可见，模拟与试验结果较为接近，说明上述建模方法较为准确，可进一步用于TYBRB力学性能的模拟分析。

4 有限元分析

4.1 模型设计

设计四组模型试件，其编号如表1 所示，TYBRB-1 为 对 照 组，TYBRB-2、TYBRB-3 和TYBRB-4 三组试件为对比组。TYBRB-2 在对照组TYBRB-1 的基础上改变R 芯板屈服段(L3段)长度，TYBRB-3 在对照组TYBRB-1 的基础上改变R 芯板非屈服段(L2段)截面积，TYBRB-4 与对照组TYBRB-1 的尺寸相同但R 芯板的屈服段(L3段)采用的钢材屈服点不同。模型中套筒、芯板连接段、芯板非屈服段及F 芯板钢材均采用Q235；TYBRB-1、TYBRB-2 和TYBRB-3 模型R 芯板、Y 芯板屈服段采用LY160；TYBRB-4 的R 芯板屈服段采用LY100，Y 芯板屈服段采用LY160。各模型试件其余具体参数如表1 所示。

表1 模型设计参数Table 1 Design parameters of specimens

对所设计的四组试件进行模拟分析，主要从TYBRB 的各项抗震性能指标对试件进行对比分析，全面评价TYBRB 的抗震性能。

4.2 滞回曲线

滞回曲线结果如图10 所示，从图10 中可看出各试件的滞回曲线都呈饱满的“梭形”，拉压基本对称，随着位移幅值增大没有出现承载能力下降及刚度退化等情况，滞回耗能能力稳定。各组TYBRB 试件滞回曲线形状基本接近，表明三阶屈服屈曲约束支撑可通过改变R 芯板屈服段长度、非屈服段面积及更换不同屈服点材料来设计目标支撑，且具备较好的耗能能力。

图10 TYBRB 滞回曲线Fig.10 Hysteretic curve of TYBRB

4.3 骨架曲线

图11(a)、图11(b)和图11(c)分别为对比组TYBRB-2、TYBRB-3 以 及TYBRB-4 与 对 照 组TYBRB-1 的骨架曲线对比图。由图11 可知，各组TYBRB 的骨架曲线均表现出明显的四折线特征，表明各组试件均实现了三阶屈服耗能。通过对骨架曲线进行分析可得，TYBRB-1、TYBRB-2、TYBRB-3 及 TYBRB-4 的 初 始 刚 度 分 别 为526.7 kN/mm、573.02 kN/mm、552.28 kN/mm 和526.61 kN/mm。相对于对照组TYBRB-1，对比组TYBRB-2、TYBRB-3 及TYBRB-4 的初始刚度分别增加了8.80%、4.86%和−0.02%。由分析可知，TYBRB 核心单元的R 芯板屈服段长度减小、非屈服段截面积增加时，TYBRB 的初始刚度增加；R 芯板屈服段采用不同屈服点钢材时，TYBRB 的初始刚度基本不变。

图11 TYBRB 骨架曲线Fig.11 Skeleton curve of TYBRB

4.4 延性系数

屈曲约束支撑作为一种金属阻尼器，不仅要有良好的滞回性能，还需具有较好的延性性质。构件的延性可以采用延性系数µ表示[19]，根据屈服位移和极限位移(本文取L/100)关系，计算得各试件的延性系数，如表2 所示。

表2 试件的延性系数Table 2 Ductility coefficient of specimens

由表2 可知，四组TYBRB 试件的延性系数均较大，表明TYBRB 屈服后仍具有较好的塑性变形能力。相较于对照组TYBRB-1，TYBRB-2、TYBRB-3和TYBRB-4 的延性系数分别增加了21.7%、10.3%、60%。由分析可知，减小R 芯板屈服段长度、增加R 芯板非屈服段的横截面面积及降低R 芯板屈服段所使用钢材的屈服点可使TYBRB 的延性系数增加，有利于增强其耗能效果。

4.5 塑性耗能能力

试件滞回曲线所包围的面积表示了试件耗能的大小，计算得到各组试件耗散能量的结果如图12 所示。

图12 试件耗散地震能量Fig.12 Seismic energy dissipation of specimens

从图12 可看出，当试件加载幅值在 ∆1y之前，TYBRB 消散地震能量值很小；当达到 ∆2y时，TYBRB-1、TYBRB-2、TYBRB-3、TYBRB-4 耗散地震能量分别为0.9 kJ、1.3 kJ、1.6 kJ 及1.5 kJ。由于 ∆2y小于多遇地震层间位移角对应的支撑位移L/1100，TYBRB 实现了小震耗能。

根据《建筑抗震试验规程》[19]规定，构件的能量耗散能力可通过能量耗散系数He进行表达，根据He的计算方法，得到各试件的能量耗散系数结果如表3 所示。

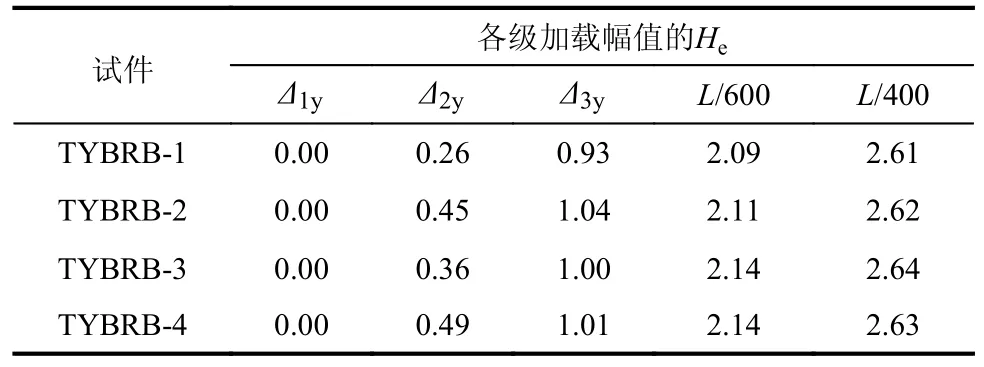
表3 试件能量耗散系数Table 3 Energy dissipation coefficients of specimens

由表3 可知，在实现一阶屈服后，TYBRB-2、TYBRB-3 和TYBRB-4 的能量耗散系数均大于对照组，说明了R 芯板屈服段长度的减小、非屈服段横截面面积的增加及屈服段钢材屈服点的降低，使TYBRB 的能量耗散系数增加，塑性耗能能力增强。

当加载幅值为 ∆2y时，改变R 芯板屈服段长度、非屈服段横截面面积以及屈服段钢材，能量耗散系数增加幅度最大。在加载幅值达到 ∆2y之后，随着加载幅值的增加，TYBRB-2、TYBRB-3以及TYBRB-4 相对对照组TYBRB-1 的能量耗散系数增加幅度逐渐减小。通过分析可知，改变各参数对TYBRB 多遇地震耗能性能增强更加明显。

4.6 等效黏性阻尼比

等效黏性阻尼比 ζ是反映结构或构件耗能性能的一个关键参数。确定等效黏性阻尼比是基于能量耗散相等的原则[20]，基于此，根据有限元结果计算得各试件的等效黏性阻尼比，如图13 所示。

图13 试件等效黏性阻尼比Fig.13 Equivalent damping ratio of specimens

当混凝土框架结构楼层位移达到弹性位移角限值θe时，近似对应支撑变形为支撑长度L的1/1100。根据图13 可知，各支撑位移加载达到其长度L的1/1100 时，四组试件均已实现第一阶、第二阶屈服，其等效黏性阻尼比都基本能够达到0.1 左右，表明试件处于塑性屈服耗能工作阶段，在结构中能增加结构的整体耗能能力，也说明了四组TYBRB 均能实现小震耗能。

图13(a)、图13(b)和图13(c)分别为对比组TYBRB-2、TYBRB-3 以 及TYBRB-4 与 对 照 组TYBRB-1 的等效黏性阻尼比对比图。由图13 可知，在不同位移幅值下，非屈服段横截面面积增加以及屈服段钢材屈服点降低，使TYBRB 的等效黏性阻尼比增大，耗能性能增强。

根据图13 中各支撑的等效黏性阻尼比结果，当支撑加载位移达到 ∆2y时，对比组与对照组结果相差最大，表明改变各对比组参数对小震下TYBRB耗能性能影响较大；此时，TYBRB-1、TYBRB-2、TYBRB-3 以 及TYBRB-4 的 ζ值 为0.041、0.072、0.057、0.078，相较于对照组，对比组TYBRB-2、TYBRB-3 以 及TYBRB-4 的 ζ值 增 加 了75.6%、39.5%、91.2%。随着加载幅值逐渐增大，对比组与对照组结果越来越接近；当支撑加载位移达到L/400 时，TYBRB-1、TYBRB-2、TYBRB-3 以及TYBRB-4 的 ζ值 为0.415、0.416、0.421、0.418，相较于对照组，对比组TYBRB-2、TYBRB-3 以及TYBRB-4 的 ζ值增加了0.2%、1.3%、0.7%。通过分析可知，R 芯板屈服段长度、非屈服段截面积及屈服段钢材屈服点的变化对支撑在小变形工况下的等效黏性阻尼比影响较大，但对位移大于L/400 工况下的等效黏性阻尼比影响很小。

5 结论

针对所提新型三阶支撑(TYBRB)，分析了其构造组成、工作机理及理论设计方法，并通过有限元模拟研究其抗震性能。主要结论如下：

(1)三阶屈服屈曲约束支撑通过R 芯板、Y 芯板、F 芯板组合实现了分阶段屈服机制，其可以在较小变形情况实现一阶、二阶屈服进行耗能，具备三阶屈服能力，在不同强度地震下可实现分阶段屈服耗能。

(2)根据三阶屈服屈曲约束支撑理论推导和数值模拟的分析结果，表明本文所提TYBRB 可以达到设计需求，且具有较好的耗能效果，说明其构造组成设计合理。

(3)三阶屈服屈曲约束支撑的延性系数相较于普通屈曲约束支撑更大，表明其塑性变形能力更强，抗震性能优越。

(4)三阶屈服屈曲约束支撑的骨架曲线呈明显的四折线特征，达到了三阶屈服的效果。三阶支撑核心单元R 芯板屈服段长度减小、非屈服段截面积增加时，其初始刚度增大；R 芯板屈服段采用不同屈服点的钢材对三阶支撑初始刚度基本无影响。

(5)数值分析表明：三阶屈服屈曲约束支撑R 芯板屈服段长度减小、非屈服段横截面面积增加以及屈服段钢材屈服点降低，使TYBRB 的能量耗散系数、等效黏性阻尼比增大，支撑耗能能力增强。TYBRB 核心单元R 芯板长度、截面积及钢材屈服点的变化对支撑在小震时的能量耗散系数、等效黏性阻尼比影响较大，但在较大地震作用时对其影响很小。