纤维拉伸曲线上屈服点的求取
孔繁荣,甘粤发,陈莉娜
(河南工程学院 纺织工程学院,河南 郑州 450007)
随着生活水平的提高,人们对纺织制品服用性能的要求也越来越高,其中拉伸性能又是影响纺织制品耐用性和服用性的重要因素。纤维受到外力拉伸至断裂时的性能通常可以用两类指标来衡量,即与拉伸曲线有关的指标和与断裂点有关的指标。与断裂点有关的指标有断裂强力、断裂强度与断裂伸长率等,均反映纤维一次拉伸至断裂时的性质,而在纺织加工和纺织品使用过程中,遇到更多的则是远小于断裂强力和断裂伸长率的拉伸。为此,有必要研究它们在拉伸过程中的应力和应变情况,这就引出与拉伸曲线有关的其他指标[1]。
与拉伸曲线有关的指标有初始模量、屈服应力、屈服伸长率、断裂功和断裂比功等,其中屈服应力和屈服伸长率为纤维在拉伸中屈服点所对应的力与变形。屈服点是在拉伸曲线上伸长变形突然变得较为容易时的转折点,一般屈服点高的纤维不易产生塑性变形,所以弹性和尺寸稳定性较好[2]。纺织材料学课程各版本教材中一般给出3种求屈服点的方法,分别为曼列狄斯法(Meredith)、考泼伦法(Coplan)和角平分线法,但均未给出纤维具体屈服点的数据。于伟东[3]曾以羊毛为例对典型拉伸曲线上力学性能指标的算法进行了归纳,但并未给出最后的计算数据,所以也无法比较不同纤维屈服点的高低,进而从屈服变化角度来比较纤维的弹性与尺寸稳定性。基于此,本研究尝试用MATLAB软件对纤维的屈服点进行求取,比较几种方法在求取屈服点时的适应性,为更好地使用屈服区域对纤维性能进行解释提供一定参考。
1 纤维拉伸过程中屈服点的求取

图1 涤纶纤维的实际拉伸曲线Fig.1 Actual tensile curve of polyester fiber
在纤维的典型拉伸曲线坡度从大变小的过程中,纤维对于变形的抵抗能力逐渐变弱,此转折点即为屈服点。常见的屈服点求取方法有曼列狄斯法、考泼伦法、角平分线法,还可以根据拉伸曲线的坡度转变用曲线方程的三阶导数来求取转变点,即三阶导数法[4]。图1为纤维在拉伸实验中所得的应力-应变曲线,使用的实验仪器为XQ-2型纤维强伸度仪,实验材料为涤纶纤维。从图1可以看出,当纤维被拉伸至断裂点后有急速下降的部分,而本研究在求取屈服点时需要连接曲线的起始位置,所以在处理实验数据时只截取断裂点之前的拉伸数据。
1.1 屈服点的求取
1.1.1曼列狄斯法
曼列狄斯法求取屈服点是在拉伸曲线上连接起始点与断裂点作一条直线,再作一条与此线平行且与拉伸曲线相切的直线,切点即所求的屈服点。将数据导入MATLAB软件,定义拉伸起始点和断裂点,将两点连接绘制一条直线并得到直线的斜率。假设一条同斜率的直线,令该直线与原拉伸曲线相切,即与原曲线有且仅有一个交点,从而得出该点的坐标,即为屈服点。经MATLAB软件运算后,在工作区输出计算结果,所求屈服点位置为(18.60,8.69),屈服应变为18.60%,屈服应力为8.69cN/tex,如图2所示。
1.1.2考泼伦法
考泼伦法是在屈服区域内找到两个近似直线的区域并作两条对应切线,两切线相交于一点,通过此点作平行于坐标系X轴的直线,交拉伸曲线于新的一点,该点即为屈服点。
将数据导入MATLAB软件,采用平均斜率法求取拉伸曲线上屈服点附近两条切线的斜率。为得到拉伸曲线上屈服区域左侧的切线(未至屈服区域),在拉伸曲线1/4处到1/3处随机选取10个点,将第1个点与第6个点、第2个点与第7个点,依次类推,直至第5个点与第10个点连接起来,得到5条直线及各自的斜率。再计算出5条直线斜率的平均值,将其作为曲线屈服区左侧切线的斜率。用此斜率在曲线上绘制出切线,同理可得屈服区域右侧切线,10个点的选择范围为拉伸曲线3/4处到2/3处。通过MATLAB软件计算出两条切线相交的点,作一条经过该点并平行于X轴的直线,交曲线于一点,此点即所求的屈服点,屈服点坐标为(21.30,9.18),即屈服应变为21.30%,屈服应力为9.18cN/tex,如图3所示。
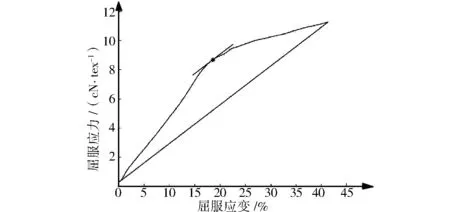
图2 曼列狄斯法求取涤纶纤维的屈服点Fig.2 Calculation of yield point of polyester fiber by Meredith method

图3 考泼伦法求取涤纶纤维的屈服点Fig.3 Calculation of yield point of polyester fiber by Coplan method
在屈服区域左右侧选择10个点时,尝试过取其他的位置如1/2处、1/10处及其他邻近屈服区域的位置,但绘制出来的两条切线或无法相切,或在同侧,导致无法求取相交点。结合纤维材料的典型拉伸曲线形状,最终在1/4处和3/4处作切线并使两条切线相交,从而完成屈服点的求取。
1.1.3角平分线法
角平分线法类似于考泼伦法,但在找到两条与曲线相切的直线后,不是找经过交点平行于X轴的直线,而是找两条直线相交后夹角的角平分线,并与拉伸曲线相交于一点,该点即为屈服点。
两条切线的求取方法与考泼伦法一样,但在求取角平分线时,利用MATLAB软件在两条切线上截取相等长度的两段,并连接形成等腰三角形。该三角形中,AB=AC,如图4所示。根据等腰三角形的中线性质,确定两条相交直线的角平分线,并通过MATLAB软件计算出与曲线相交的点,屈服点坐标为(18.82,8.73),即屈服应变为18.82%,屈服应力为8.73cN/tex,如图5所示。

图4 等腰三角形求取角平分线Fig.4 Obtaining bisector of angle by isosceles triangle

图5 角平分线法求取涤纶纤维的屈服点Fig.5 Calculation of yield point of polyester fiber by angular bisector
1.1.4三阶导数法
三阶导数法是通过屈服点的定义来求取屈服点,对拉伸曲线方程进行3次求导,然后求出与X轴的交点,该点即对应的屈服点。三阶导数需对拉伸曲线方程进行求导,但实验仪器得到的拉伸曲线并没有给出相应的方程,故将拉伸过程的实验数据通过MATLAB软件绘制出拉伸曲线,并进行曲线方程的拟合,再对拟合方程进行求导以得到屈服点。导入数据后,绘制拉伸曲线,选用Fourier方程进行拟合,如图6所示。因为要进行3次求导,所以在次数项处选择4次,即可得到完整的拟合方程,求导后得到与X轴的交点为12.819 2%,查找数据得屈服应变率为12.82%,屈服应力为5.78cN/tex。
1.2 求取方法的适应性
上述4种方法均可求取得到屈服点,但结果之间具有差异,其原因是纤维的拉伸过程中屈服变化为一个区域,并且4种方法的原理也不同。
曼列狄斯法是4种方法中最容易得到屈服点的方法,且对拉伸曲线形状没有要求。通过连接拉伸起始点与断裂点即可求出两点间的斜率,从而作一条斜率相同的直线相切于屈服点。
考泼伦法和角平分线法均比曼列狄斯法要复杂一些,前期确定两条相切直线的方法相同。求取过程中为了确定两条切线斜率,需要分别在曲线的1/4处和3/4处各取10个点,两两连接10个点得到5条直线的斜率,再使用5条直线的平均斜率得到拉伸曲线的切线,1/4处和3/4处为实验中根据典型拉伸曲线的形状和不断实验得到的经验值,同时在每处的周围只随机选取10个点进行计算,所以结果存在一定的误差。在求取过程中,有一些拉伸曲线与典型拉伸曲线形状差异较大,曲线中的应力或应变有突然增加或减少的趋势,或者纤维的拉伸过程较短,从曲线上看不出明显的屈服变化,这会导致两条切线无法相交,从而无法完成后续步骤以求取屈服点,如图7所示。

图6 Fourier拟合拉伸曲线Fig.6 Fitting tensile curve by Fourier
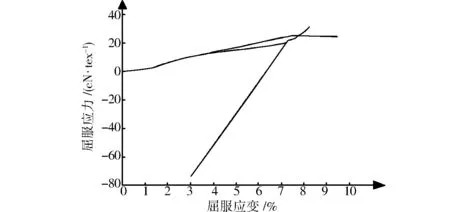
图7 非典型拉伸曲线Fig.7 A typical tensile curve
三阶导数法从原理上应该更接近屈服区域的起始位置,但该方法是基于拉伸曲线的方程式求导得到的,目前从拉伸实验仪中只能得到拉伸的数据,无法直接得到原拉伸曲线的函数关系式,所以方程的拟合就决定了求导的结果,不同的纤维材料拉伸数据差异较大,所以采用此方法时选择什么样的函数进行拟合比较重要,但对原拉伸曲线的形状并无要求。
2 结语
本研究提到的4种方法均可以得到纤维在拉伸过程中的屈服点,不同方法得到的具体值有所不同,并无可比性。曼列狄斯法的适应性较强,任何形状的拉伸曲线均可绘制出切线,并求出屈服点;考泼伦法和角平分线法由于要在屈服区域两侧做切线,在实际求取时如果拉伸曲线的变化和典型拉伸曲线相差较大,或者本身屈服区域不明显,则屈服点的求取较为困难;三阶导数法需要采用纤维的原始拉伸数据进行拉伸曲线的拟合并获取函数关系式,从而求导得到屈服点,拟合函数的选择和拟合程度会直接影响屈服点的求取,但对纤维的拉伸过程并无要求,借助计算机可以快速准确地获得屈服点。

