基于Simscape Multibody的六自由度机器人运动轨迹规划误差分析

黄宏俊 ，姜羽飞

(1.河南工程学院 工程训练中心，河南 郑州 451191；2.郑州理工职业学院 机电工程系，河南 郑州441500)

工业机器人是科技进步与发展的代表性成果，也是多学科、多领域的综合产物。我国工业机器人的需求量约占全球的三分之一[1]。在工业机器人的研究中，最重要的是轨迹研究。早在1983年，Lin等[2]首次研究机器人在三次多项式下的轨迹优化；1991年，Wang等[3]又研究出一种求解机械臂逆运动学问题的组合优化方法；2015年，Gasparetto等[4]对机器人轨迹规划算法给出了概述。

针对运动学轨迹的研究，各个领域都有学者在不断探索。其中，关于工业机器人轨迹的研究一般分为两类，一类是基于关节坐标系来规划工业机器人的轨迹，另一类则是在笛卡尔坐标系下进行工业机器人轨迹的规划。唐越等[5]利用正向运动学对工业机器人进行了关节空间轨迹规划；王沐雨等[6]使用MATLAB Robotic工具箱对ABB IRB1600型工业机器人在关节坐标系下的运动进行了仿真研究；王晓明等[7]从逆向运动学方面对工业机器人进行轨迹规划并利用 MATLAB Robotic工具箱对机器人轨迹进行了仿真；朱志伟等[8]对KUKA R1420型焊接机器人在关节空间中的焊接轨迹进行了规划；郭青阳[9]对KUKA焊接机器人定位误差进行分析并提出了补偿方法。

目前，机器人轨迹研究已成为机器人研究的热点，而类似于KUKA KR6型的六轴工业机器人却在运动中存在轨迹误差。因此，实际应用中的轨迹往往与理论规划的轨迹计算值不符，但利用MATLAB Robotic工具箱无法得到运动输入与输出变化。基于以上问题，本研究利用Simscape Multibody对该类型工业机器人理想规划轨迹进行系统仿真，在可视化环境下检测出仿真实际运动轨迹，对实际检测轨迹与计算输入的目标轨迹之间的误差规律进行总结，并对生产提出了合理建议。

1 机器人运动学建模分析

对KUKA KR6型工业机器人进行三维建模，模型如图1所示。该机器人有6个关节，同时也有6个连杆，由此可以看出该机器人具有六自由度。

在研究过程中，首先利用D-H法对工业机器人关节进行数学建模。根据机器人各关节与各连杆的关系，在笛卡尔空间作出相应的坐标系，以关节轴线为Z轴，指向末端操作器方向为X轴，通过右手定则来判断Y轴，可以得到空间中的坐标系，由下至上分别对应每个关节连杆，其中X0、Y0、Z0坐标系为基准坐标系，如图2 所示。

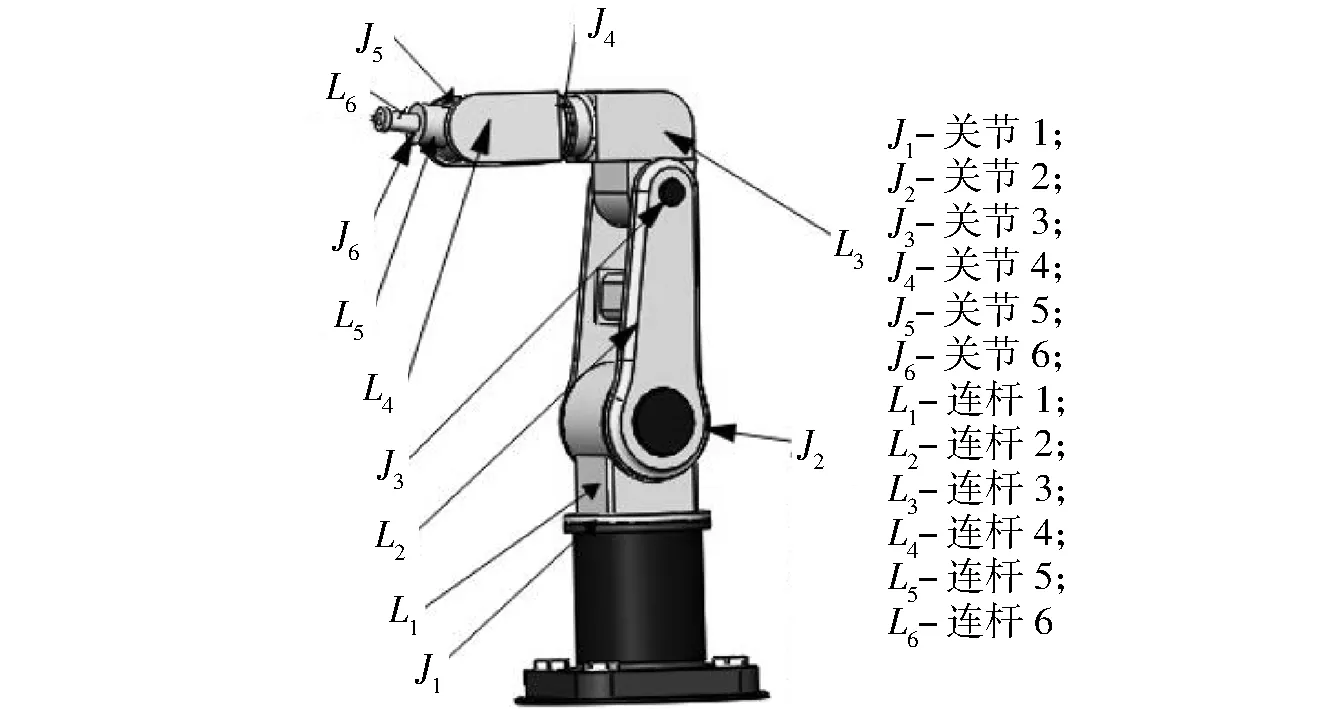
图1 六轴机器人三维模型Fig.1 6-axis robot 3D model

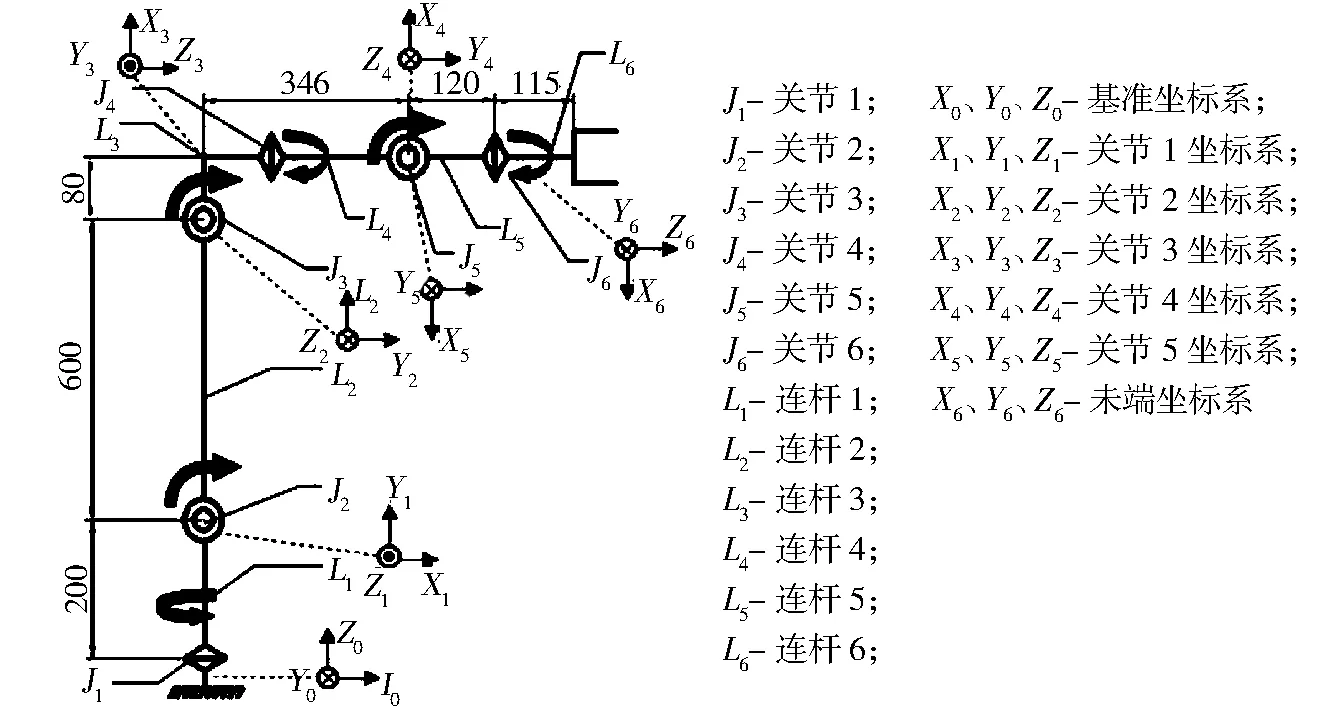
图2 机器人坐标系Fig.2 Robot coordinate system

根据各个连杆关节的相互关系建立D-H参数表，如表1所示。其中，θj表示关节扭角，aj表示连杆长度，αj表示相邻连杆间扭转角，dj表示关节偏距，以顺时针旋转方向为正方向。

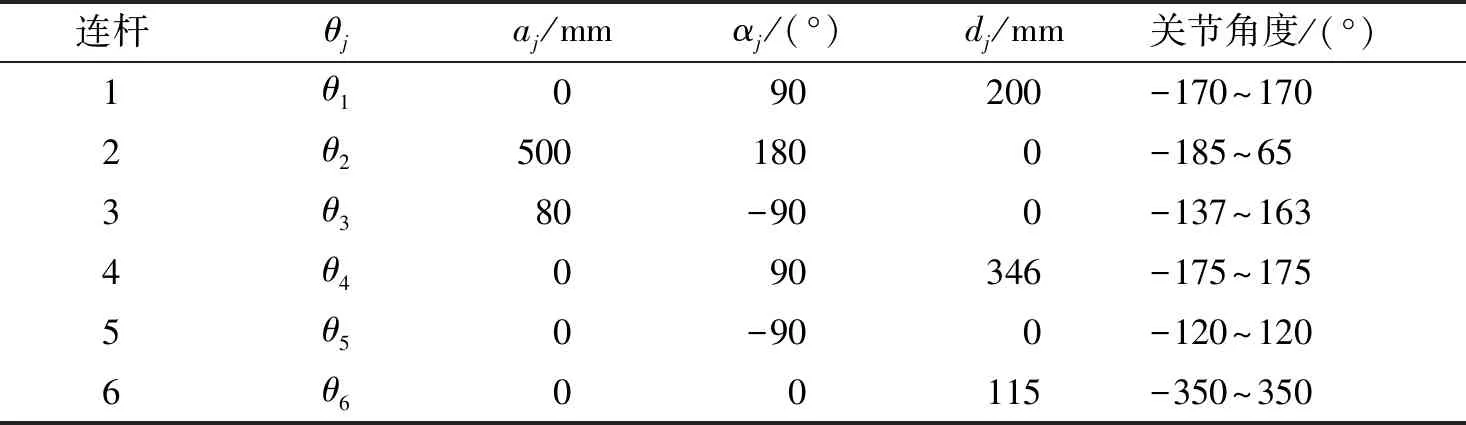
表1 D-H参数Tab.1 D-H parameters

通过D-H法可得到各个关节之间的位置关系，继而可进行正向运动学推导。相邻两连杆之间的齐次变换矩阵为

(1)

式中：c代表余弦函数cos(θ)；s代表正弦函数sin(θ)；R为旋转齐次变换矩阵；T为平移齐次变换矩阵；n-1Tn表示连杆坐标系之间的齐次矩阵。

将D-H参数代入公式(1)中，经过6次迭代可推导出末端操作器位姿。末端操作器位姿矩阵如下：

(2)

在公式(2)中，各个元素可分别对应结果(结果中省略乘号)：

nx=sθ6[cθ4(sθ1-cθ1sθ2)-sθ4(cθ1sθ2sθ3+cθ1cθ2cθ3)+cθ1cθ2sθ3-cθ1cθ3sθ2]-cθ6{sθ5(cθ1cθ2sθ3-

cθ1cθ3sθ2)-cθ5[cθ4(cθ1sθ2sθ3+cθ1cθ2cθ3)+sθ4(sθ1-cθ1sθ2)]}，

ox=sθ6{sθ5(cθ1cθ2sθ3-cθ1cθ3sθ2)-cθ5[cθ4(cθ1sθ2sθ3+cθ1cθ2cθ3)+sθ4(sθ1-cθ1sθ2)]}+

cθ6[cθ4(sθ1-cθ1sθ2)-sθ4(cθ1sθ2sθ3+cθ1cθ2cθ3)+cθ1cθ2sθ3-cθ1cθ3sθ2]，

ax=-sθ5[cθ4(cθ1sθ2sθ3+cθ1cθ2cθ3)+sθ4(sθ1-cθ1sθ2)]-cθ5(cθ1cθ2sθ3-cθ1cθ3sθ2)，

px=500cθ1-115sθ5[cθ4(cθ1sθ2sθ3+cθ1cθ2cθ3)+sθ4(sθ1-cθ1sθ2)]}-

115cθ5(cθ1cθ2sθ3-cθ1cθ3sθ2)-346cθ1cθ2sθ3+346cθ1cθ2sθ3+180cθ1sθ2sθ3+180cθ1cθ2cθ3，

ny=sθ6[cθ4(cθ1+sθ1sθ2)+sθ4(cθ2cθ3sθ1+sθ1scθ2sθ3)-cθ2sθ1sθ3+cθ3sθ2sθ1] -

cθ6{cθ5[sθ4(cθ1+sθ1sθ2)-cθ4(cθ2cθ3sθ1+sθ1scθ2sθ3)]+sθ5(cθ2sθ1sθ3-cθ3sθ1sθ2)}，

oy=sθ6{cθ5[sθ4(cθ1+sθ1sθ2)-cθ4(cθ2cθ3sθ1+sθ1scθ2sθ3)]+sθ5(cθ2sθ1sθ3-cθ3sθ1sθ2)}-

cθ6[cθ4(cθ1+sθ1sθ2)+sθ4(cθ2cθ3sθ1+sθ1sθ2sθ3)-cθ2sθ1sθ3+cθ3sθ1sθ2]，

αy=sθ5[sθ4(cθ1+sθ1sθ2)-cθ4(cθ2cθ3sθ1+sθ1sθ2sθ3)]-cθ5(cθ2sθ1sθ3-cθ3sθ1sθ2)，

py=115sθ5[sθ4(cθ1+sθ1sθ2)-cθ4(cθ2cθ3sθ1+sθ1sθ2sθθ3)]+500cθ2sθ1-

115cθ5(cθ2sθ1sθ3-cθ3sθ1sθ2)+180cθ2cθ3sθ1-346cθ2sθ1sθ3+346cθ3sθ1sθ2+180sθ1sθ2sθ3，

nz=cθ6[sθ5(cθ3sθ2-sθ2sθ3)+cθ4cθ5(cθ3sθ2+sθ2sθ3)]-sθ6[sθ4(cθ3sθ2+sθ2θ3)+cθ3sθ2-sθ2sθ3]，

oz=-sθ6[sθ5(cθ3sθ2-sθ2sθ3)+cθ4cθ5(cθ3sθ2+sθ2sθ3)]-cθ6[sθ4(cθ3sθ2+sθ2sθ3)+cθ3sθ2-sθ2sθ3]，

az=cθ5(cθ3sθ2-sθ2sθ3)-cθ4sθ5(cθ3sθ2+sθ2sθ3)，

pz=500sθ2+526cθ3sθ2-166sθ2sθ3+115cθ5(cθ3sθ2-sθ2sθ3)-115cθ4sθ5(cθ3sθ2+sθ2sθ3)+200。

2 运动轨迹规划

2.1 设定轨迹起始点与轨迹目标点

关节空间轨迹规划的第一步是设定起始点与目标点。轨迹规划过程中关注的往往是末端操作器的运动轨迹，即末端操作器运动状态的改变。如果在关节空间中进行轨迹规划，首先要设定末端操作器的起始点姿态与目标点姿态，利用逆运动学方程解出每个关节的运动角度，从而将末端操作器在笛卡尔空间中的姿态变化问题转化为关节空间中各个关节角度随规定时间变化的问题。基于三角读法表示出末端操作器在初始状态下与目标状态下的位姿，其中参数a、b、c表示以ZXZ方式整合的欧拉角，参数x、y、z表示在笛卡尔坐标系方向的位移，具体如表2所示。

表2 末端操作器初始状态下与目标状态下的位姿Tab.2 End manipulator posture in initial and target states

2.2 轨迹规划方程

对六自由度工业机器人进行数学建模后，要求工业机器人末端操作器由一个初始位置点移动到目标位置点，各关节运动速度要求平滑。

本研究采用五次多项式插值对机器人运动过程中的参数进行设置。在关节空间的运动规划中，已知机器人的初始点末端位姿与目标点末端位姿，计算初始末端位置对应角度θ0与目标末端位置对应角度θf，再设定当时间为0～tf时，应用逆向运动学求得其余关节的角度，规划出关节运动轨迹。同时，为使关节运动轨迹连续光滑，关节变量采用五次多项式进行插值，轨迹规划条件如下：

(3)

式中：θ(t)为关节角度变化函数。

基于初始条件式(3)，对运动初始位姿对应的关节角度与运动目标位置的关节角度轨迹进行插值，设定一个以时间t为变量的五次多项式：

θ(t)=a0+a1t+a2t2+a3t3+a4t4+a5t5。

(4)

基于式(4)，可以继续求导得到关节的速度与加速度方程：

(5)

基于初始条件式(3)，由式(4)和式(5)可推导出五次方程组特定矩阵形式：

(6)

根据式(6)，代入各个关节初始角度值和运动时间内的角度值。设定运动时间为20 s，可得到规划关节方程组：

(7)

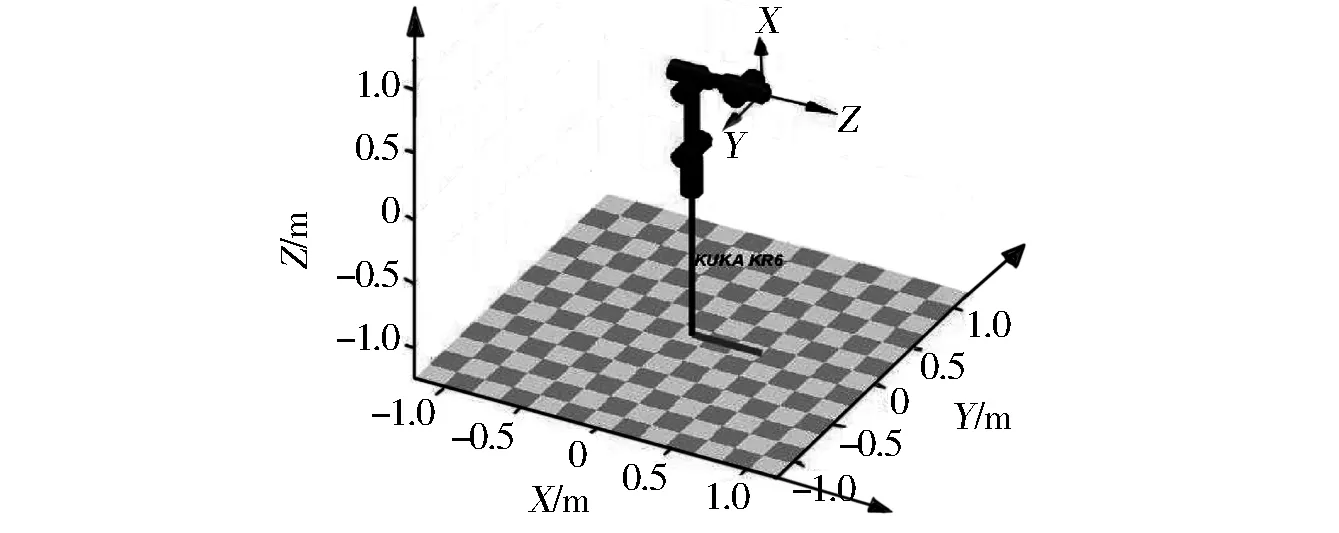
图3 MATLAB中的机器人模型Fig.3 Robot model in MATLAB

2.3 运动轨迹插值及图像

已知运动轨迹起始点、目标点与运动轨迹方程，本研究采用Peter Corke提供的MATLAB Robotic开源工具箱进行数值运算，得到相应的轨迹规划参数。

根据机器人数学模型及D-H参数，可以在机器人工具箱中建立对应的机器人模型，如图3所示。

建立模型后,在关节空间下还需要确定已知初始点与目标点的空间角。根据表2可以得到工业机器人末端位姿,由于欧拉角旋转按照ZXZ序列方式进行，故在Robotic工具箱中使用内置函数A=eul2r(a,b,c)，其中a、b、c为表2中的旋转角度，并将转换后的矩阵赋于变量A中，x、y、z为末端位姿原点坐标。得到末端操作器在初始点与目标点的位姿后，通过机器人逆向运动学可计算出各个关节的不同角度值，利用Robotic工具箱中自带的求逆运动学解函数B=ikine(A)得到一组解且赋于变量B中，在该解中可得到初始关节角度。同理，可得末端关节角度。

由已知条件可得，初始各关节角度分别为θ1=π、θ2=π/2、θ3=-π/4、θ4=π、θ5=-π/2、θ6=0，目标点各个关节角度为θ1=π/3、θ2=π/3、θ3=0、θ4=0、θ5=-π/3、θ6=π/2。

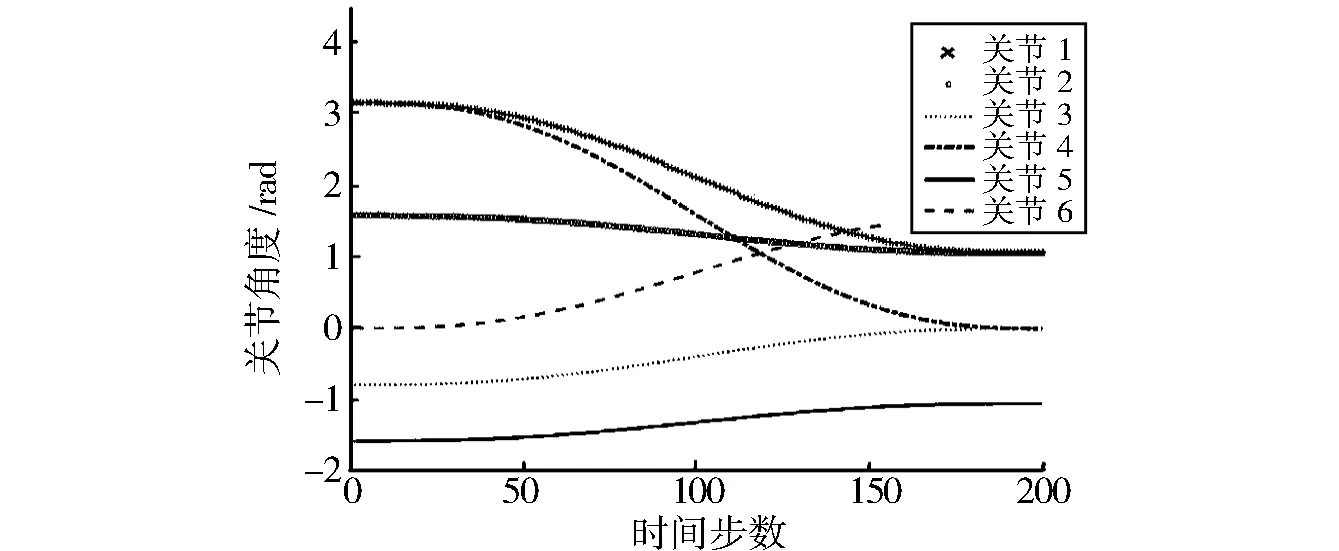
图4 关节运动轨迹曲线Fig.4 Joint trajectory curve

最终在已知初始位置关节角度与末端位置关节角度下，可通过函数[q,qd,qdd]=jtarj(C,D,step)进行计算,其中C、D分别为初始各关节角度与目标位置各关节角度,step表示时间步数，q表示关节角度，qd表示关节角速度，qdd表示关节角加速度。MATLAB在进行轨迹运算时，只能用离散变量来代替连续变量，step越大，表示运算中间点越多、迭代次数越多，同时轨迹方程曲线也就越光滑。

在确定的时间内进行仿真，时间步数选择200，图4为关节运动轨迹曲线，图5为关节角速度在规定时间内的变化曲线，图6为关节角加速度的运动变化曲线。

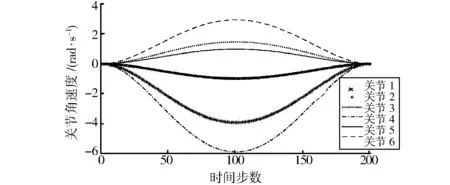
图5 关节角速度曲线Fig.5 Speed image of each join

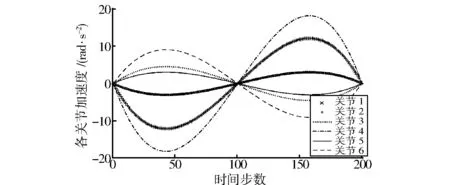
图6 关节加速度曲线Fig.6 Joint acceleration curve

3 运动轨迹仿真与误差分析

3.1 模型可视化仿真

利用SolidWorks软件建立三维模型后，将三维模型导入Simulink软件，在Simulink软件中自动生成Multibody环境，在仿真模型中加入输入/输出模块，具体如图7所示。

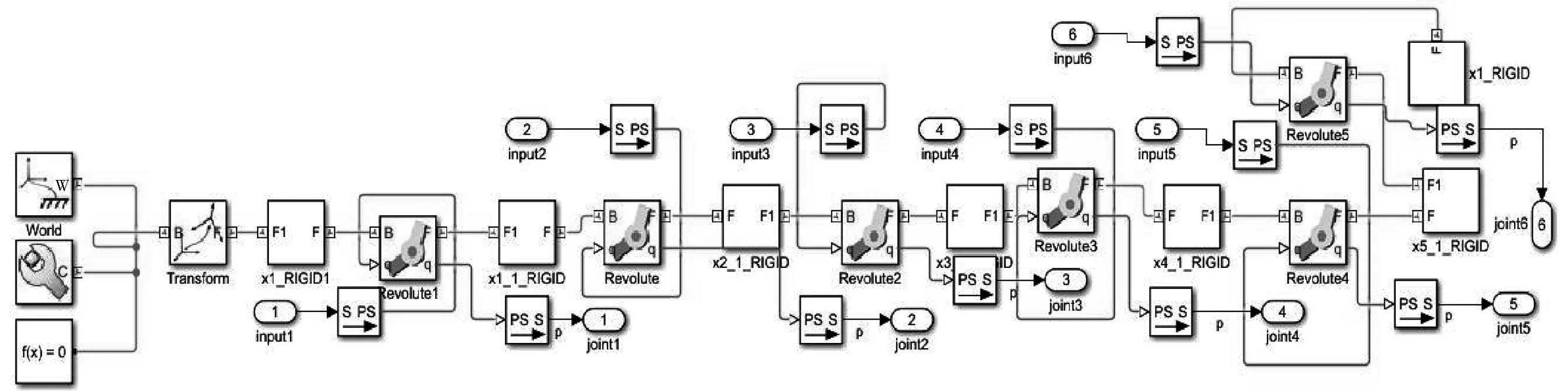
图7 Simscape Multibody环境下的系统仿真模型Fig.7 System simulation model under Simscape Multibody

输入参数为6个关节位置角度随时间变化的运动轨迹方程(7)，运动仿真时间设定为20 s，由于设定运动步数为200，可推导出每隔0.1 s对运动曲线进行中间点插值，将已规划好的5次方轨迹最终导入模型中，可经过Simulink仿真观测三维模型的运动轨迹。

图8为由MTALAB Robotic工具箱计算的末端操作器在笛卡尔空间内的运动轨迹，该轨迹在笛卡尔空间内表示为一条直线。图9为目标位置下的Simscape Multibody模型窗口。经Simscape Multibody可视化仿真后，模型基本符合运动轨迹。

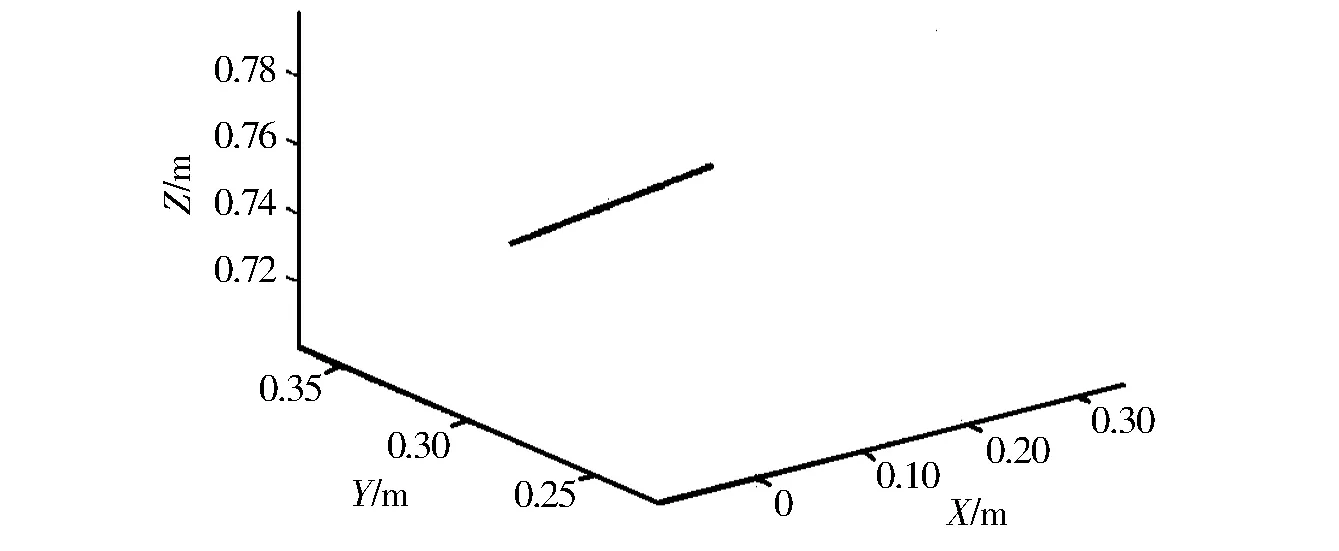
图8 笛卡尔空间仿真运动轨迹Fig.8 Cartesian space trajectory

图9 Simscape Multibody模型窗口Fig.9 Simscape Multibody model window

3.2 运动轨迹误差分析

图10为规划轨迹与仿真轨迹的误差带，关节曲线代表理论计算规划的轨迹与利用Simscape Multibody模块仿真出的轨迹。

图11为轨迹误差的变化曲线。由图11可知，轨迹误差随时间的变化呈抛物线，每个轨迹从起始位置到目标位置附近时，轨迹运动的误差非常小，说明关节扰动量很小，在5～15 s扰动量最大，而在起始与终止的时间段，误差逐渐减少。这个过程中的关节运动误差见表3。

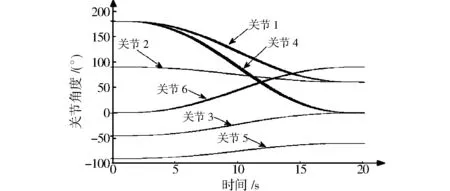
图10 规划轨迹与仿真轨迹的误差带Fig.10 Error graph of planned and simulated trajectory

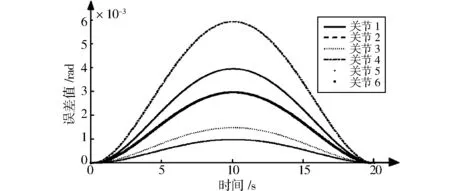
图11 轨迹误差变化曲线Fig.11 Histogram of trajectory errors

表3 关节运动误差Tab.3 Joint motion errors

3.3 实测误差分析

仿真模型为理想状态下机器人的运动轨迹，而实际工作环境下机器人的运动轨迹与仿真模型的运动轨迹存在误差，基于KUKA工作台对机器人运动时的轨迹点进行取样，利用示教器进行编程，使得实际工作环境下的机器人在关节空间下进行PTP运动。

图12是各个关节实际误差的4次方拟合曲线。经过实测可得出，机器人在关节空间下运动时始终存在误差。在机器人进行PTP运动时，由于机器人在标定过程中关注于末端点位置，于是产生一定的标定误差，又因为运动轨迹中的误差先增加后又通过自带算法补偿，故使得后半段运动过程中的误差减少。误差值与仿真误差不同，但误差规律基本相同。

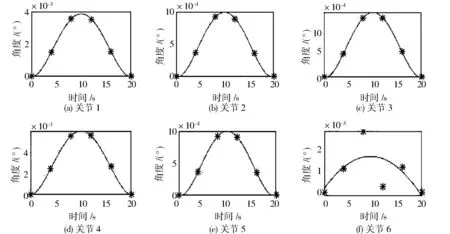
图12 各关节实际误差的4次方拟合曲线Fig.12 The quadruplicate fitting curve of the actual error of each joint

4 结语

本研究以KUKA KR6机器人为原型，对机器人进行关节轨迹规划，利用MATLAB Robotic开源工具箱计算规划数值，最终在Simscape Multibody中进行仿真。在仿真结果中可以实时看到模型在计算轨迹中的动态变化，并可得到实际轨迹与计算输入轨迹的误差，即在运动到中间点附近时轨迹误差值最大，而初始点与末端点附近的误差值最小。在实际运动过程中，误差随时间变化而变化，在运动到中间时间点时，误差值最大。

在实际应用中，机器人在由起始点到终止点的运动过程中，存在标定误差、零点误差、机械公差、减速器误差等一系列误差。为保证机器人运动轨迹精确，对于短距离运动而言，这些轨迹误差很小、可适当忽略，而对于长距离且需要高精度轨迹的情况，有两种方式可减少误差，一种是改善算法、增加标定点以实时追踪运动轨迹，另一种是在编程过程中增加中间点来进行过渡，使运动轨迹更加清晰，这样可以最大限度地减少运动过程中的误差、保证运动轨迹的精确。