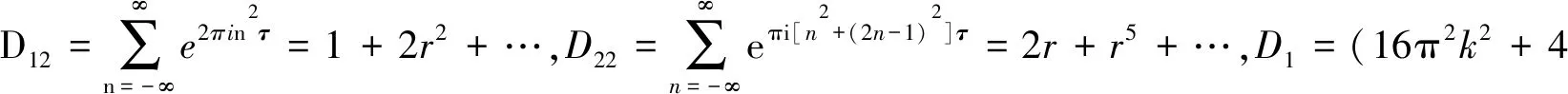(2+1) 维Boussinesq方程的黎曼theta函数周期波解

王 辉，苏 婷

(河南工程学院 理学院, 河南 郑州 451191)

对非线性方程精确解的探讨在整个非线性物理现象的研究中占有重要地位。例如在流体力学、等离子体和弹性介质中观察到的波动现象通常可由钟形sech解和扭结形tanh行波解模拟出来。这些非线性方程的精确解(如果有的话)有助于数值解的验证，并且有助于解的稳定性分析。在过去的几十年中，这些方法取得了显著的进展，如著名的逆散射变换[1-2]、贝克隆变换和达布变换[3-5]、李群方法[6-7]、Hirota双线性方法[8-11]、穿衣方法[12-14]、Painleve分析[15-16]等。

1 问题的提出

著名的Boussinesq方程是描述浅水中色散和非线性的一类波动方程，该方程的色散关系介于浅水中的非色散、非线性长波与Stoke色散波之间，故它在水波运动、早期气体预测、海洋环境保护等领域得到了广泛的应用。Ma等[17]利用第2个Wronskian公式研究了(1+1)维Boussinesq方程，得到了各种解。文献[18]中的Wazwaz研究了六阶(1+1)维Boussinesq方程的多孤子解。Yang等[19]应用Riccati展开法研究了广义(2+1)维Boussinesq方程。

本研究将要介绍一个新的六阶(2+1)维Boussinesq方程：

(1)

方程(1)描述的也是一个浅水波。在第2节中，通过适当变换得到了该方程的双线性形式，借助于扰动法，可以得到该方程的一孤子解。在第3节中，利用黎曼theta函数性质和双线性导数法，进一步得到了该方程的黎曼theta函数周期波解，并且在最后研究了这个周期波解的渐近性质。

2 双线性形式

为了得到方程(1)的双线性形式，首先引入一个变换：

u=2(lnρ)xx。

(2)

将变换(2)代入方程(1)中并且积分两次，则方程(1)就变成如下双线性形式：

(3)

式中：c为积分常数。算子D在文献[9]中定义为

(4)

式(4)中的m、n为非负整数。对于指数函数，D有如下重要结论：

(5)

取c=0，求方程(3)的一孤子解。利用扰动法，设

ρ=1+ερ1+ε2ρ2+ε3ρ3+…,

(6)

式中：ε是一个小参数。

令

ρ1=expθ1，θ1=k1x+p1y+ω1t+θ10，

(7)

(8)

3 黎曼theta函数周期波解及渐近性态

根据方程(1)的双线性导数形式，借助多维黎曼theta函数性质，可以得到方程(1)的黎曼theta函数一周期波解，并且在最后讨论了该解的渐近性态。

3.1 黎曼theta函数周期波解

结合代数几何知识[20]，黎曼theta函数形式如下：

(9)

式中：n=(n1,…，nN)，ζ=(ζ1，…，ζN),τ是一个对称矩阵且有正定的虚部,ζj=kjx+ρjy+ωjt+ζj,j=1,…,N。

接下来求一周期波解，取N=1,则式(9)就简化为

(10)

将式(10)代入式(3)中，有

(11)

事实上，

(12)

(13)

取一些记号：

(14)

则式(12)和(13)就简化为

D11(ω2+2p2)+D12c+D1=0，D21(ω2+2p2)+D22c+D2=0，

(15)

(16)

(17)

因此，得到了黎曼theta函数周期波解

(18)

图 1和图2分别表示上述黎曼theta函数周期波解(18)在某一时刻的三维图像与沿着x轴方向的二维平面曲线(用Mathematica软件绘制)，其中k1=2、p1=4、ω1=6、τ=2i、θ01=0、t=10。

图1 周期波解的三维图像Fig.1 The one-periodic solution in 3

图2 周期波解沿着x轴方向的图像Fig.2 The one-periodic solution along x-axis

3.2 黎曼theta函数周期波解的渐近性态

本节验证前面得到的一孤子解(8)正好是黎曼theta函数周期解(18)的渐近结果。

定理1当Imτ→∞方程(3)的周期波解(9)趋近类似于式(8)形式的单子孤解时，

(19)

(20)

证明记r=eπiτ，则v、vx及vxx可以写成如下形式(Imτ→∞)：

借助于变换(2)，可以得到形式为式(18)的解。下面验证式(19)和式(20)成立。事实上