基于带约束的修正梯形加速度规律规划算法研究

叶增林，陈 华，吴 昊

(马鞍山学院 人工智能创新学院，安徽 马鞍山 243100)

加减速控制算法是机器人控制系统插补器的重要组成部分，也是运动控制领域的关键技术之一。合理的加减速控制算法在实际的机器人运动控制系统中可提高机器人运行效率，减少机器人本体的振动和冲击。目前在机器人运动控制系统中，梯形速度规划算法和S型速度规划算法较为常用。梯形速度的规划方式由于加速度的不连续变化会引起机构的振动和冲击[1-2]。S型速度规划算法因其速度曲线类似字母“S”的形状而得名，其加速度曲线规律为梯形，在机器人和高精度的数控加工系统中被广泛应用[3]。在运动控制系统中一般采用加速度连续变化的位移曲线，而S型速度曲线光滑，加速度曲线连续，能有效减少冲击和振动，非常适用于高速高精的运动控制场合[4-7]。目前国内外学者已经对S型速度曲线进行了详细的研究[8-11]。Jahanpour等[12]研究了一种基于S型速度曲线的规划算法，但是该算法未考虑固定路径约束会对规划的速度参数产生一定影响。段晓斌等[13]提出了一种基于Gutman运动规律的修正梯形速度曲线机器人轨迹规划方法，解决了普通S型速度规划中加加速度不连续的问题，但是该方法计算量较大，增加了控制器的计算负担，并且没有考虑给定最大速度对规划的影响。

本研究根据机器人运动规划对加减速曲线的基本要求，提出了一种具有速度与加速度约束且带有修正系数的梯形加速度规律规划算法，对于给定的速度与加速度约束，基于时间判别法将该段规划划分为对应的加速度规律类型，从而来调整速度与加速度之间的适配关系。将算法编成软件并采用8组给定的约束参数进行仿真实验，验证了本算法的合理性与有效性。

1 修正梯形加速度规律的加减速曲线

1.1 修正梯形加减速曲线构造

在常用的七段式加速度规律的基础上加入修正系数n，加速度规律由加加速段、匀加速段、减加速段、匀速段、加减速段、匀减速段、减减速段构成，图1为加减速全过程中的位移、速度及加速度曲线。

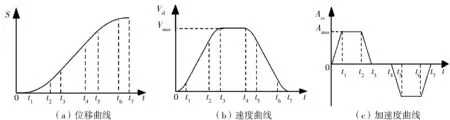
图1 修正梯形加减速曲线Fig.1 Modified trapezoidal acceleration and deceleration curve

图1中，0～t7为整个加减速规划的周期，时间记为T。0～t1表示分段时刻，为加加速阶段，时间记为nT,其中n为梯形加速度的修正系数；t1～t2为匀加速阶段，时间记为T0；t3～t4为匀速阶段，时间记为T1。通过推导可以得到修正梯形加减速全过程的加速度A、速度V及位移S的公式，分别如式(1)、(2)、(3)所示：

(1)

(2)

(3)

式中：T=4nT+2T0+T1；Amax为给定的最大加速度。

1.2 修正梯形加速度规律的特性分析

由图1和式(1)～(3)可知：该七段式加速度规律由加速、匀速和减速3部分组成；加速部分的加加速和减加速的加速度图形是对称分布的，即t1=t3-t2=nT，匀加速部分的时间t2-t1=T0；匀速部分的时间t4-t3=T1;减速部分与加速部分的图形是关于t3和t4的中点对称的，即t5-t4=t7-t6=nT，t6-t5=T0。

从图1中可以看出，该加减速规律中的加速度曲线连续，速度曲线平滑过渡，三阶公式计算量较小，是一种良好的运动控制规划规律，并且该规划规律中引入了修正系数n，在实际的动态规划中可根据给定的位移和规划总时间及时调整规划的加减速段时间，从而减少机构的振动与冲击。但在实际的规划应用中，由于给定的位移、最大速度和最大加速度的不确定性，会导致规划规律中没有图1中的匀加速或匀速段等情况。

接下来将提出一种基于时间判别法的梯形加速度规划算法，该算法可根据给定的参数来划分规划类型并自动适配加速度与速度参数，并可针对小位移、大加速度的约束参数调整修正系数，并对最大速度和最大加速度进行约束，从而达到良好的控制效果。

2 基于时间判别法的梯形加速度规划

首先将给定的位移、最大速度和最大加速度参数代入式(4)，计算对于该段位移的规划总时间T：

(4)

由于后续规划采用等时插补的方式，所以为保证插补的完整性，在此需要对计算出的规划总时间T进行处理后代入式(5)，计算得到新的T：

(5)

式中：Δt为后续等时插补的时间间隔；ceil为向上取整函数。采用该方法处理可保证后续等时插补的完整性，即保证位移的精度。由于对总时间T做出了微小的调整，所以在此将T作为已知参数代入式(6)，计算新的最大加速度参数：

(6)

将新的加速度与时间参数代入式(7)，即可求得匀加速段时间T0和匀速段时间T1：

(7)

以上所有计算都是在假定规划规律为七段式梯形加速度规律的基础上进行的，但由于给定参数的不确定性，如果将所有路径一律按照七段式梯形加速度规律进行规划，那么在某些给定参数的情况下将会导致计算出错而无法进行规划。因此，对上述基于七段式梯形加速度规律计算得到的T0和T1进行分析，根据分析结果将不同的给定参数按照相对的梯形加速度规律进行规划。

图2 六段式加速度规律Fig.2 Six-segment acceleration law

类型一：七段式加速度规律。若T0>0、T1>0，则在给定的距离S范围内可以达到最大加速度Amax和最大速度Vmax，采用七段式加速度规律进行规划，即如图1中所示规律和采用上述公式进行计算。

类型二：六段式加速度规律。若T0>0、T1<0，则表明在给定的距离S范围内以当前的最大加速度Amax无法达到以最大速度Vmax进行匀速运动。在此，令T1=0，采用六段式加速度规律进行规划，加减速曲线规律如图2所示。将给定的Amax代入式(8)中进行计算，得到新的时间T和新的速度Vnew参数：

(8)

类型三：五段式加速度规律。若T0<0、T1>0，则表明在给定的距离S范围内无法达到最大加速度Amax进行匀加速运动，但可达到给定的最大速度Vmax匀速运行。在此令T0=0，采用五段式加速度规律进行规划，加减速曲线规律如图3所示。将给定的Vmax代入式(9)中进行计算，得到新的时间T和加速度Anew参数：

图3 五段式加速度规律Fig.3 Five-segment acceleration law

(9)

分析式(7)可得，不可能出现T0<0和T1<0的情况，所以对于规划的分类主要有以上3种。但对于机器人实际运行情况中给定较小的位移和较大的加速度参数来说，将会出现如下两种情况：(1)由于给定的最大速度参数较小，在给定的较小位移S内能以最大加速度参数加速到最大速度，随后保持最大速度匀速运行一段时间，属于类型三。但由于位移小、加速度较大，会在很短时间内加速到最大速度，导致机构的过冲与振动。(2)由于给定的最大速度参数较大，在给定的较小位移S内无法以最大加速度参数加速到最大速度，但仍以给定的最大加速度参数加速到一个新的最大速度，属于类型二。同样，在较小位移时采用较大的加速度参数会导致机构的过冲。

因此，在针对此种情况进行规划时，若给定的总位移小于加加速段和减加速段产生的位移的2倍，即S<2S1，则采用四段式加速度规律，此时T0=0、T1=0、n=0.25，加减速曲线规律如图4所示。

图4 四段式加速度规律Fig.4 Four-segment acceleration law

将给定的Amax和Vmax代入式(10)中进行计算，根据时间参数调整加速度与速度参数，从而得到新的速度Vmax和加速度Anew：

(10)

图5 时间判别法规划流程Fig.5 Flow chart of time discriminant planning

综上所述，针对给定的位移S、最大速度Vmax和最大加速度Amax约束参数，利用常用的七段式加速度规律规划进行计算，根据计算得到的匀加速段时间T0和匀速段时间T1，判别不同的给定约束参数适用于哪种加速度规律，并对速度和加速度参数进行适配。另外，针对位移较小和加速度较大的情况，利用位移进行判别，若符合类型四的规划规律，则对规划总时间进行调整并对加速度和速度根据时间和位移进行适配，从而获得较好的规划曲线。规划流程如图5所示。

3 规划仿真

采用软件编制程序，对该规划算法进行仿真验证，仿真中采用的参数设定如表1所示，得到的结果如图6所示。将图1和图6对比可知，图1中为普通七段式加速度规律曲线，而在图6的仿真曲线中可以看出，本算法对于给定的位移、速度与加速度参数，可自动判别且选择类型进行规划，并对给定的速度和加速度进行适配处理，构成了良好的运动规律曲线；对于给定的位移较小和加速度较大的情况，该算法可自动选择四段式加速度规律进行规划，并对给定的较大加速度进行约束处理，从而有效避免了机构的冲击振动。例如图6中的(g)和(h)，针对位移较小、加速度大和速度较大的情况，算法自动进行四段式规划，从而适当增加了加减速时间，有效地缓解了加减速冲击。

表1 修正梯形加速度仿真验证参数Tab.1 Modified trapezoidal acceleration simulation verification parameters

图6 速度和加速度约束的修正梯形规律仿真验证Fig.6 Simulation verification diagram of the modified trapezoidal law of velocity and acceleration constraints

4 结论

(1)基于位移、最大速度和最大加速度约束提出了一种带有速度和加速度约束的修正梯形加速度规律规划算法，通过时间判别法对给定的约束参数自动选择规划类型，并对速度和加速度自动适配。针对位移小、加速度大的约束，自动调整修正系数，并对速度和加速度进行约束处理，有效减少了冲击与振动。(2)仿真结果表明该算法能够让给定的最大速度和加速度参数在规划中起到约束作用，并根据不同的给定参数自动选择规划类型并对参数进行调整适配。另外，该算法计算量较小，可提高运动插补器的实时性，具有简单、高效的特点。