转子系统结构参数对碟式分离机动力学特性的影响研究
徐 鹏,赵理志,吴建军,丁 毅,田宇琦,詹 远,侯天柱
(1.海装沈阳局驻大连地区第一军事代表室,辽宁 大连 116000) (2.中交烟台环保疏浚有限公司,山东 烟台 264000) (3.中交(天津)疏浚工程有限公司,天津 300451) (4.中国船舶集团有限公司第七一一研究所,上海 201108)
碟式分离机基于重力沉降槽发展而来,利用离心作用下混合液中具有不同密度,互不相溶的轻、重液相和固体具有不同沉降速度的原理,达到分离分层或使固体颗粒沉降的目的[1],具有结构紧凑、分离效率高、自动化程度高、连续作业能力强的特点,在食品加工、医药工业、化学工业、石油工业等行业被广泛地应用[2-3]。
为实现大的分离因数,碟式分离机常设计较高的工作转速。当工作转速高于转子系统的一阶临界转速时,转子系统为柔性转子,其动力学特性对系统能否安全稳定地工作至关重要[4-6]。现有研究表明:当工作转速接近临界转速时,系统容易产生共振,严重时可能引起系统结构的破坏。改变转子系统的支承条件,可直接影响系统的临界转速,同时也会对系统的不平衡响应产生影响[7-10]。
碟式分离机的动力学特性与转子系统的结构参数直接相关,本文利用DyRoBeS软件建立某型碟式分离机的转子系统模型,在此基础上探究不同的结构参数对碟式分离机动力学特性的影响,为碟式分离机的设计提供依据和参考。
1 计算模型
1.1 物理模型
简化后的某型碟式分离机的高速转子系统基本结构尺寸如图1所示。整体采用悬浮支承结构,上端由深沟球轴承支承,下端由双列调心滚子轴承支承。深沟球轴承周围均布有4个复合弹簧,即沿x向、y向在轴承两端各布置一个复合弹簧,在工作过程中,复合弹簧与深沟球轴承之间始终有预压力,不会脱离。调心滚子轴承上方有恒力作用,作用方向为x向或y向。转鼓体内充满液体,视为一个整体,不考虑内部液体的影响。主轴及转鼓体材料均为双相不锈钢,牌号为00Cr22Ni5Mo3N。
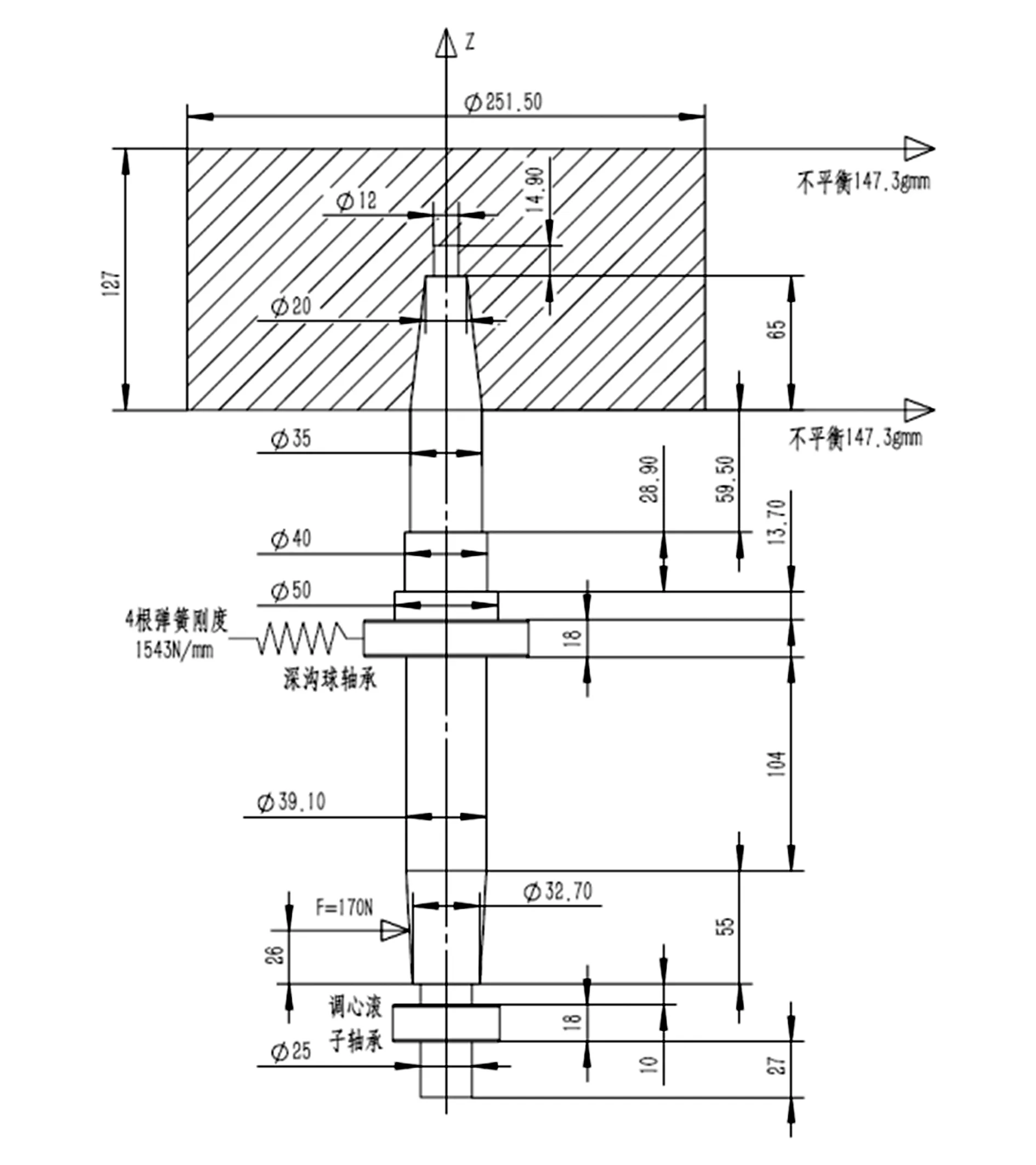
图1 碟式分离机转子系统结构简化图
1.2 DyRoBeS模型
在DyRoBeS中根据其建模规则,建立某型碟式分离机的高速转子系统基础模型,如图2所示。上端深沟球轴承位于节点9处,下端调心滚子轴承位于节点3处,根据轴承的具体型号计算对应轴承刚度,在一定的受力范围内,非线性的滚动轴承刚度变化不大,可简化轴承的刚度为定值。复合弹簧一端与节点9连接,另一端固定,设置复合弹簧刚度值。恒力作用于节点6处,不平衡力作用于节点13与节点15处。z向设置有重力加速度g。
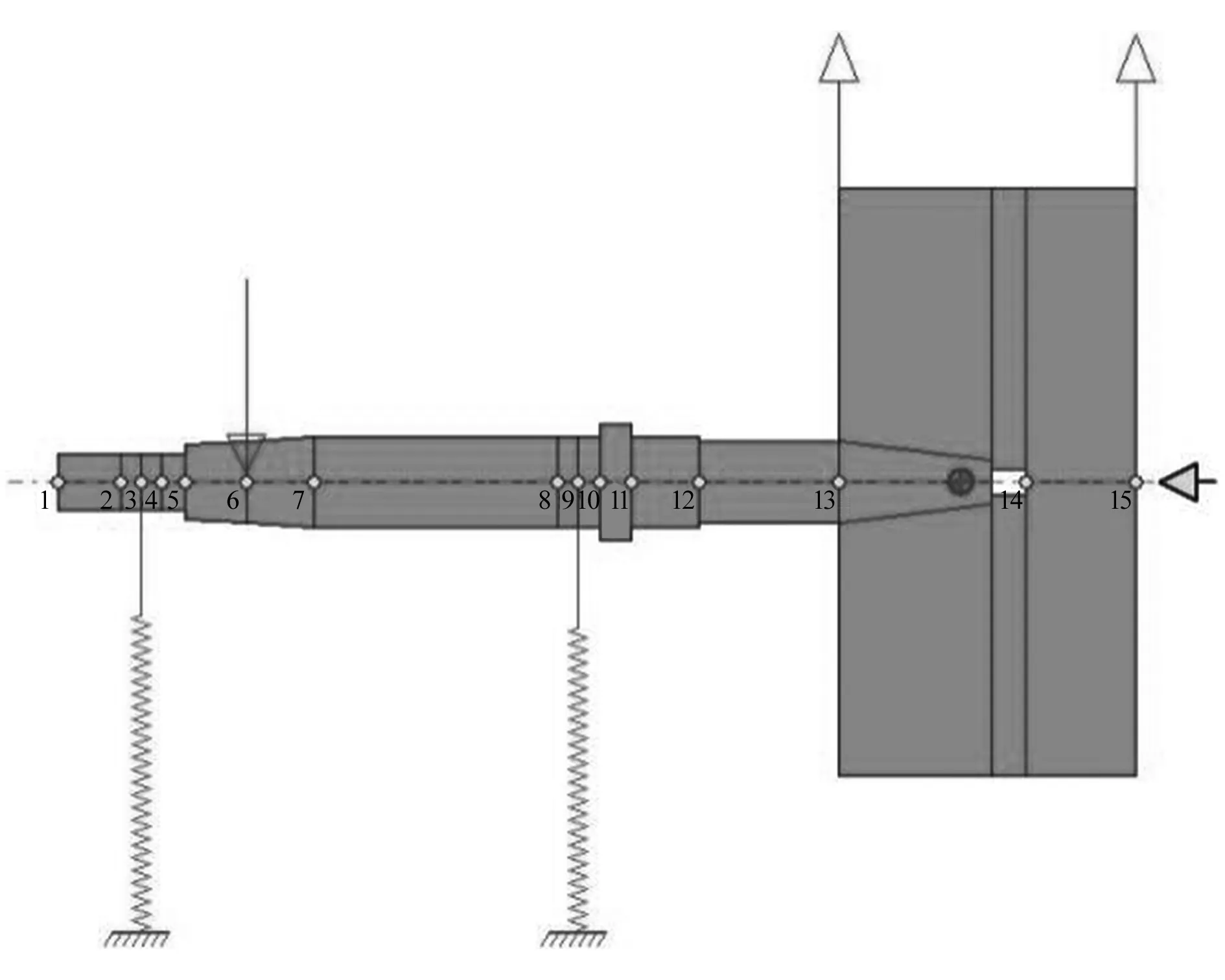
图2 碟式分离机转子系统DyRoBeS模型
2 工况设置
本文着重研究碟式分离机动力学特性随支承刚度、支承跨距、悬臂长度的变化规律,针对每一个结构参数均设置有5个工况点,通过对计算结果的对比分析,了解相应参数变化时动力学特性的变化趋势。各工况设置的参数见表1。

表1 参数设置表
3 结果分析
本文探究的碟式分离机动力学特性主要包括3个方面,分别为轴系临界转速、轴系不平衡响应以及轴系应力。
转鼓处的振幅大小直接关系到碟式分离机的性能,故选取转鼓质心处节点作为参考点,考察各参数变化对轴系不平衡响应的影响。
根据DyRoBeS的仿真结果,碟式分离机轴系的主要模态弯曲应力集中在上支承对应节点处,而模态剪切应力集中在下支承对应节点处,选取对应节点作为参考点,考察各参数变化对轴系应力的影响。
3.1 支承刚度对动力学特性的影响
改变支承刚度,即改变复合弹簧的刚度,保持其余结构参数不变,进行碟式分离机轴系临界转速、不平衡响应及应力的计算。
3.1.1支承刚度对轴系临界转速的影响
碟式分离机的上支承采用4个复合弹簧的挠性支承结构,降低了系统的结构刚度,不同支承刚度下,DyRoBeS模型计算的对应一阶临界转速如图3所示。可以看出,碟式分离机轴系的一阶临界转速随支承刚度的增加而增大。当复合弹簧刚度由3 086 000 N/m增加到5 000 000 N/m时,临界转速由1 244 r/min上升至1 540 r/min,上升幅度明显。
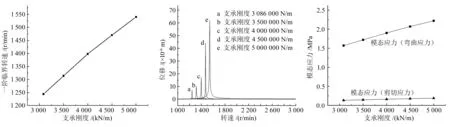
图3 支承刚度对临界转速的影响曲线 图4 支承刚度对不平衡响应的影响曲线 图5 支承刚度对应力的影响曲线
3.1.2支承刚度对轴系不平衡响应的影响
不同支承刚度下,DyRoBeS模型计算的参考点处不平衡响应结果如图4所示。可以看出,不同支承刚度对应的响应曲线均有一个明显的峰值,其对应转速即为临界转速,图4反映出的支承刚度对轴系一阶临界转速的影响规律与前文一致。同时,随着支承刚度的增加,轴系不平衡响应的峰值也逐渐增大。
3.1.3支承刚度对轴系应力的影响
不同支承刚度下,DyRoBeS模型计算的轴系应力结果如图5所示。可以看出,轴系的弯曲与剪切应力均随支承刚度的增加而增大,应力总体水平较低,主要受到弯曲应力的影响。
3.2 支承跨距对动力学特性的影响
改变两支承间的距离,保持其余结构参数不变,进行碟式分离机轴系临界转速、不平衡响应及应力的计算。
3.2.1支承跨距对轴系临界转速的影响
不同支承跨距下,DyRoBeS模型计算的对应一阶临界转速如图6所示。可以看出,随着支承跨距的增加,一阶临界转速增大。碟式分离机转子系统为悬臂结构,增加支承跨距,缩短了悬臂长度,轴系整体的刚度增加,引起临界转速的上升。
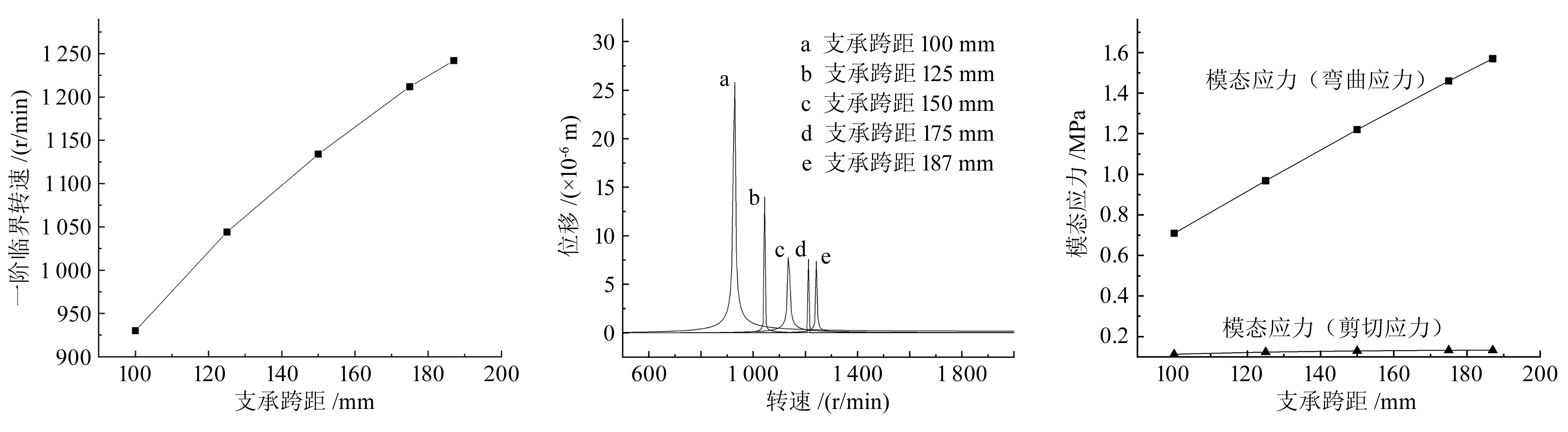
图6 支承跨距对临界转速的影响曲线 图7 支承跨距对不平衡响应的影响曲线 图8 支承跨距对应力的影响曲线
3.2.2支承跨距对轴系不平衡响应的影响
不同支承跨距下,DyRoBeS模型计算的参考点处不平衡响应结果如图7所示。可以看出,增加支承跨距,对应不平衡响应曲线的峰值向右移动,峰值也随之降低,这是增加支承跨距使轴系整体刚度增大的结果。
3.2.3支承跨距对轴系应力的影响
不同支承跨距下,DyRoBeS模型计算的轴系应力结果如图8所示。可以看出,轴系应力随支承跨距的增加而增大,主要受弯曲应力的影响,应力总体水平较低。
3.3 悬臂长度对动力学特性的影响
改变转子系统转鼓体的悬臂长度,保持其余结构参数不变,进行碟式分离机轴系临界转速、不平衡响应及应力的计算。
3.3.1悬臂长度对轴系临界转速的影响
不同悬臂长度下,DyRoBeS模型计算的对应一阶临界转速如图9所示。可以看出,随着悬臂长度的增加,一阶临界转速降低。分析可知,悬臂长度增加使轴系整体刚度减弱,导致一阶临界转速降低[11]。
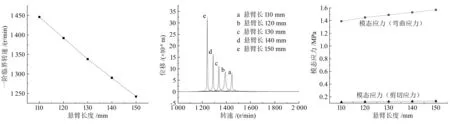
图9 悬臂长度对临界转速的影响曲线 图10 悬臂长度对不平衡响应的影响曲线 图11 悬臂长度对应力的影响曲线
3.3.2悬臂长度对轴系不平衡响应的影响
不同悬臂长度下,DyRoBeS模型计算的参考点处不平衡响应结果如图10所示。可以看出,随着悬臂长度的增加,轴系的不平衡响应峰值向左移动,峰值也随之增大,这与增加悬臂长度使轴系整体刚度降低造成的影响相吻合。
3.3.3悬臂长度对轴系应力的影响
不同悬臂长度下,DyRoBeS模型计算的轴系应力结果如图11所示。可以看出,轴系的应力分布随着悬臂长度的增加而增大,轴系的应力主要为弯曲应力,总体的应力较小。
4 结论
本文以某型碟式分离机为对象,基于DyRoBeS建立其高速转子系统分析模型,用控制变量法研究支承刚度、支承跨距、悬臂长度等结构参数对碟式分离机动力学特性的影响,结论如下:
1)碟式分离机的一阶临界转速随支承刚度、支承跨距的增加而增大,随悬臂长度的增加而减小。
2)碟式分离机的不平衡响应峰值随支承刚度、悬臂长度的增加而增大,随支承跨距的增加而减小;峰值对应转速随支承刚度、支承跨距的增加而升高,随悬臂长度的增加而降低。
3)碟式分离机的轴系应力随支承刚度、支承跨距及悬臂长度的增加均呈现出增大的趋势,但轴系整体的应力水平较低。
在进行碟式分离机转子系统设计时,可通过调整支承刚度、支承跨距及悬臂长度等参数,得到合理的轴系临界转速、不平衡响应和应力。

