某自动步枪击发机构参数化分析与优化设计

贾陆阳,景春温,刘万川,吴胜光,李东昊

(重庆建设工业(集团)有限责任公司,重庆 400054)

自动步枪在射击时,通过击锤打击击针,击针打击底火,引起底火变形,将能量传递给击发药,击发药受到挤压引燃发射药[1]。某型自动步枪采用击锤回转式击发机构,击锤在复进簧的作用下作回转运动打击击针,完成击发。击发机构的工作状况不仅影响武器工作的可靠性,还对精度产生一定的影响。因此研究击发机构参数对击发能量、底火变形量的影响,对提高武器工作的可靠性有重要意义。

在对机械式击发机构的研究中,高岩[2]对转管武器击发机构的机构可靠性与结构可靠性进行了仿真分析。葛藤等[3]对第二发弹的击发机理和击发底火的力学过程进行了仿真研究。杨九州等[4]对枪弹的击发过程进行了仿真分析。蔺月敬[5]利用有限元法,建立火炮击发机构的刚柔耦合模型,并结合理论分析找到了击发机构的薄弱部位。王红梅等[6]采用理论与有限元仿真相结合的方法,对击发机构撞击过程中的击锤与击针进行能量分析,计算了击锤与击针撞击时的能量损失,在工程应用方面打下了基础,对击发机构能量损失的研究有一定的参考价值。

1 击发机构运动建模

1.1 基本假设

为了研究击发机构击发过程,基于击发工作原理,做出如下假设:

1)击发机构运动可简化为6个自由度的刚体运动,即随质心的3个平动和绕质心的3个转动;

2)击发机构仿真过程中,将弹壳、机头体设置固定不动;

3)击锤与击针的碰撞为弹性碰撞。

1.2 结构描述

本文研究对象为某步枪的击发机构,如图1所示,由击锤、击锤簧、击针、机头和弹丸等组成,击锤在击锤簧的作用下作回转运动以打击击针,完成击发。击发机构在工作中,击针撞击底火瞬间必须具有足够的动能E,才能可靠地点燃底火。

图1 击发机构工作示意图

根据击发机构的工作情况,得到击发机构的拓扑关系,如图2所示。

图2 击发机构拓扑关系

1.3 击发机构运动分析

在击发机构仿真中,建立不同零件的相对坐标系,通过坐标系描述不同零件之间的相对运动关系[7]。在击发机构中存在多个碰撞接触,包括击锤击针之间的碰撞接触、击针与底火之间的碰撞接触等。为了保证击发机构在建模过程中的准确性,需要对击发机构中产生的碰撞接触进行分析。

在击锤簧的作用下,击锤簧带动击锤做回转运动,击锤与击针碰撞,随着击针位移的增大,底火的变形不断增大,击针的能量转化为底火的变形能。在射击过程中,击针与底火的撞击速度太大,击发机构会出现漏烟、击针断裂等故障;撞击速度太小,击发机构会出现不发火故障,因此,需要合理设计击发机构的各个结构参数。

1.4 接触碰撞力模型

1)法向接触力模型。

击发机构在碰撞过程中,两个零件之间的碰撞速度、材料参数、零件尺寸等因素,对碰撞有很大影响。本文选择Lankarani-Nikravesh接触力模型[8]描述法向接触力:

(1)

阻尼系数C可表示为:

(2)

2)摩擦力模型。

击发机构工作过程中,两个零件之间发生接触碰撞,应考虑两个零件之间相对运动时产生的摩擦力,零件之间的摩擦力对击锤、击针速度有很大影响。仿真过程中,考虑摩擦力的影响,一般采用修正的Coulomb摩擦模型[9-10],可以将两个零件之间产生的摩擦力准确地描述出来。切向摩擦力Ft可以表示为:

(3)

式中:cf为滑动摩擦系数,cd为动态修正系数,vt为相对切向速度。

动态修正系数cd可以表示为:

(4)

式中:v0和v1为计算动态校正系数而指定的速度值。

1.5 击发能量分析

1)击锤簧的能量转化。

该步枪击发机构为击锤回转式打击击针,击锤簧的弹性势能转化为击锤的动能,能量转化过程为:

(5)

式中:J0为击锤回转轴O的转动惯量,mc为击锤质量,r0为击锤回转半径,r为击锤回转轴O至击锤质量替换点的距离。

击锤运动方程为:

(6)

式中:T2为扭簧的工作扭矩,T′为扭转刚度,β为击锤某瞬时角加速度,ω为击锤某瞬时角速度,Φ为击锤转动角度,t为时间。

对击锤参数进行求解:

(7)

式中:Φi为i时刻的击锤转动角度,ωi为i时刻的击锤角速度,h为步长。

2) 击锤的能量转化。

击针撞击底火壳能量有以下两种情况:

①击针与底火壳撞击,击锤与击针碰撞后分离,击针的动能转化为底火壳的变形能,击发能量计算公式为:

(8)

击针打底火时的能量E1的计算公式为:

(9)

②击锤与击针撞击后结合,击发能量E2的计算公式为:

(10)

由武器撞击动力学可知,碰撞后分离计算的底火壳能量小于碰撞后结合的底火壳能量。将两种情况下计算得到的底火壳能量与实际射击进行对比,可知碰撞后结合比碰撞后分离更符合实际情况。

将击针撞击底火的能量转化为底火的变形能,即击发机构的击发能量,计算公式为:

Ej=aE0

(11)

式中:Ej为击发机构的变形能,即击发能量;a为比例系数;E0为击锤的初始动能。

2 击发机构优化设计

2.1 击发机构设计参数

击发机构在击发过程中,击针与机头的碰撞、击锤与击针的碰撞、击针与弹壳的碰撞,会影响击针能量的变化,从而影响底火是否能够100%击发。因此,为了提高击发机构正常击发的可靠性,应调整击发机构参数,在保证底火能够100%击发的条件下,底火变形能最小。

击发机构在实际工作中,由于工作环境不同,会导致击发机构零件之间存在差异性,因此每次击发时,击发机构的初始条件都存在差异。考虑随机因素对其的影响,将设计变量X分为非随机变化的Xd与随机变化的设计变量Xp[11]。

根据击发机构动力学的相关理论,影响击发机构的主要结构参数有击锤质量m1、击针质量m2、击锤簧刚度系数K、击锤簧预压力F、击锤簧阻尼ξ、击针凸出量L。其他结构参数,如机头与击针的定位接触面等,由于本身的取值变化并不大,因此可直接确定。

将需要优化的参数记为设计变量X,设计变量表示成向量的形式为:

X=[m1,m2,K,F,ξ,L]T

(12)

非随机变化的设计变量Xd包括K、L,表示成向量的形式为:

Xd=[K,L]T

(13)

Xp包括m1、m2、F、ξ,表示成向量的形式为:

Xp=[m1,m2,F,ξ]T

(14)

2.2 击发机构优化模型

优化目标为底火壳变形能,即目标参数为能够保证底火100%击发时底火壳能的最小值,并以此为目标函数。击发机构模型以击针撞击弹壳,击针速度为0时为结束信号。

考虑参数随机性的击发机构优化问题可以表示为:

Xd,μxp

(15)

Xd,min≤Xd≤Xd,max

Xp,min+hσxp≤μxp≤Xp,max-hσxp

2.3 优化算法及优化流程

击发机构优化的基本思想如下:确定击发机构的设计变量,并确定其设计变量范围,根据优化算法,依据设计变量范围与分布,对其进行采样,选取一组数据作为样本数据,然后调用模型,分别代入所采集的样本点数据进行计算。应用上述的采样方法,在设计变量范围内循环取样,进行下一组计算[12-13]。

击发机构进行优化分析时,将优化流程分为全局优化与梯度优化[14]。击发机构优化过程中,根据数据参数产生随机样本量,分析其规律。优化过程中产生随机值的组合,并得到对应的目标值,选取最优值所对应的随机点组合,即为最优解。本文采用拉丁超立方试验设计的方法[15-16],提高计算效率,优化流程如图3所示。

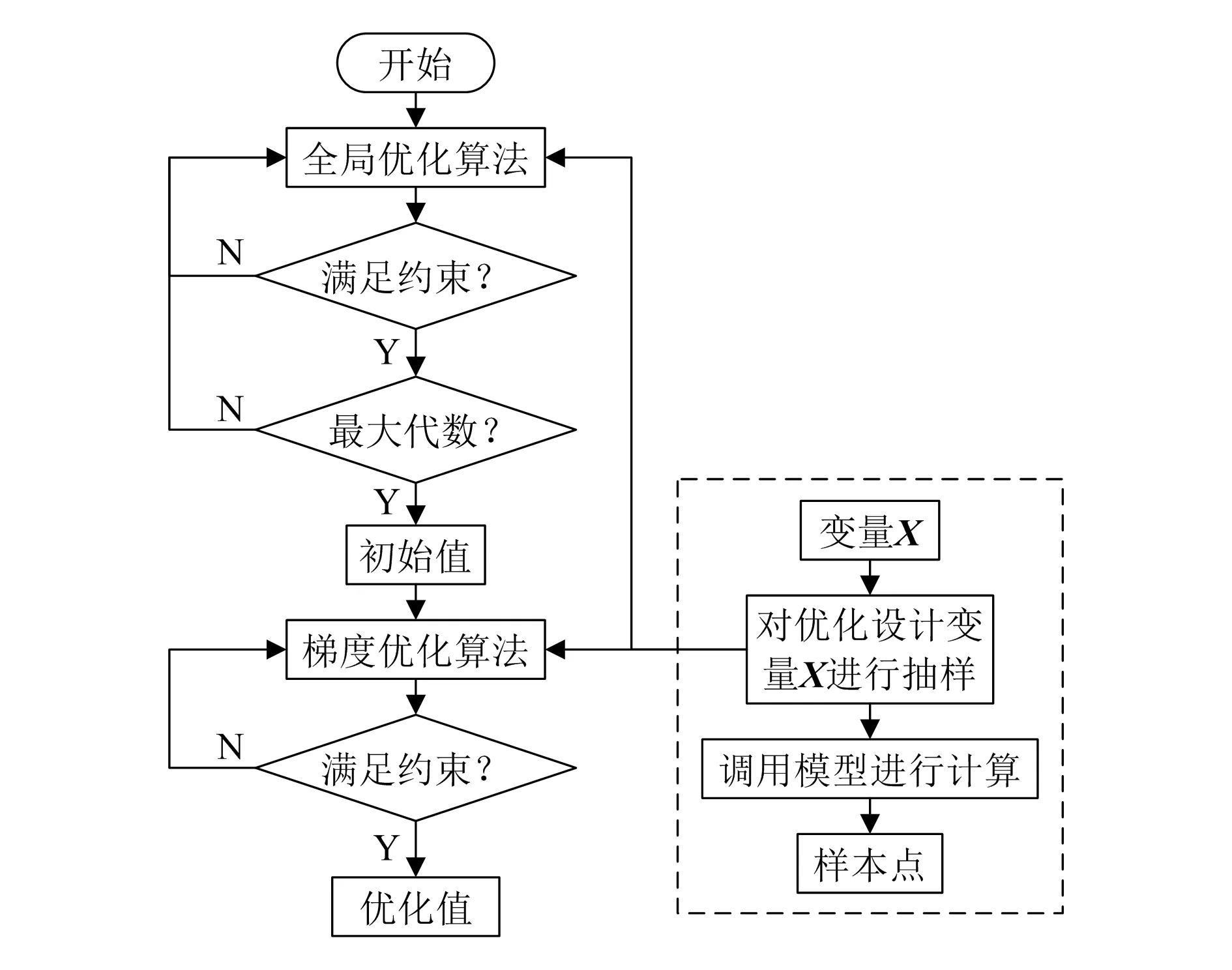
图3 击发机构优化流程图

3 算例分析

基于上述分析和假设,在ADAMS[17]中建立某步枪击发机构动力学模型。表1所示为击发机构不确定性输入参数,这些参数均服从正态分布。

表1 击发机构不确定性输入参数

将表1中的初始参数值(表中的名义值)代入击发机构动力学模型中进行仿真分析,得到击锤角速度、击锤动能的变化情况,击针动能的变化情况。由图4、图5可以看出,击锤在击锤簧的作用下,击锤的角速度与能量在逐渐增加,当击锤打击击针后,击锤与击针一起运动,最后击针作用在底火上,将击针的动能转化为底火的变形能。击锤打击击针后,击针动能变化如图6所示。由于不确定参数的存在,击发机构击针的能量也变为不确定参数。因此,需合理设计输入参数,优化击发机构底火的变形能。

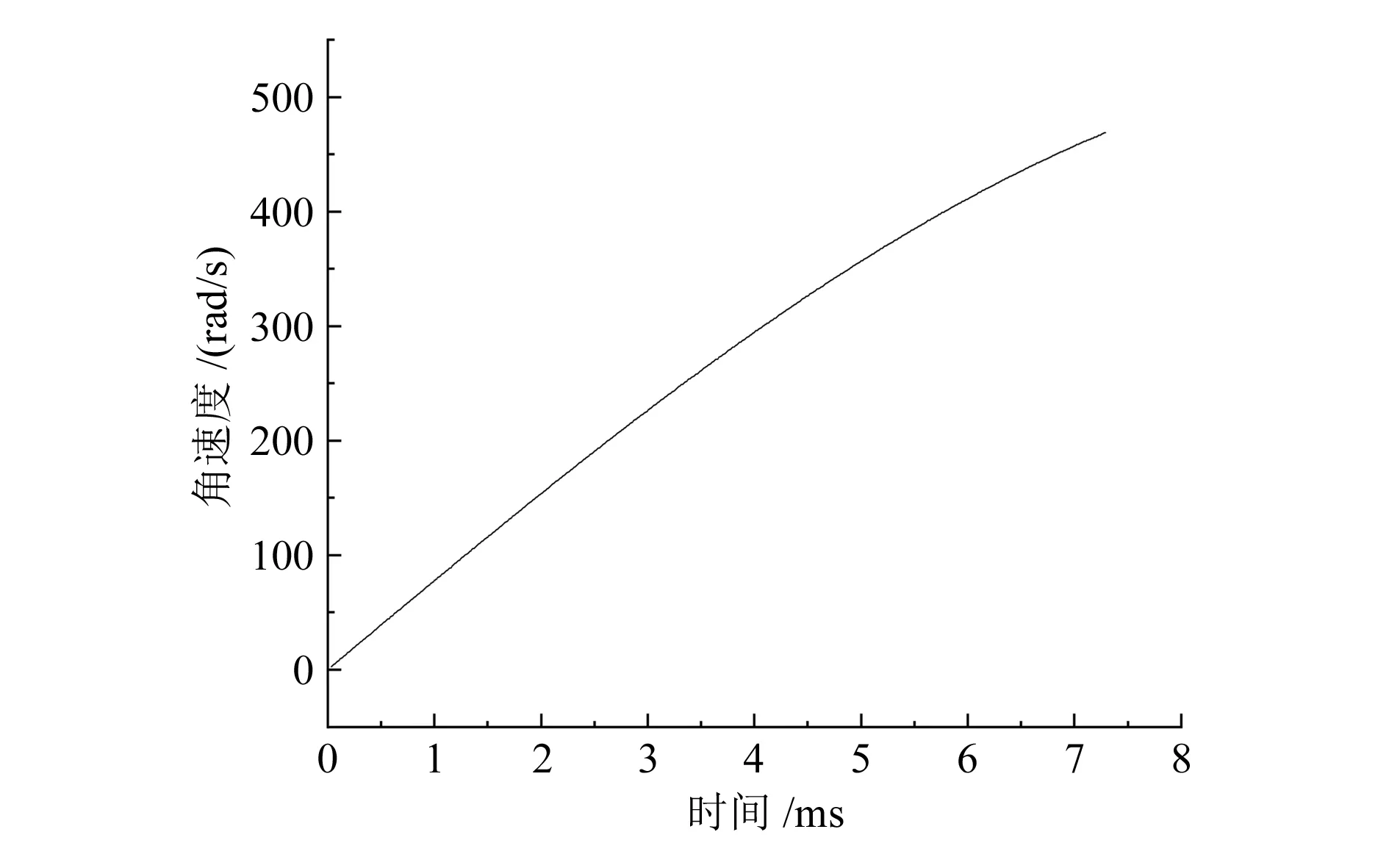
图4 击锤角速度变化曲线

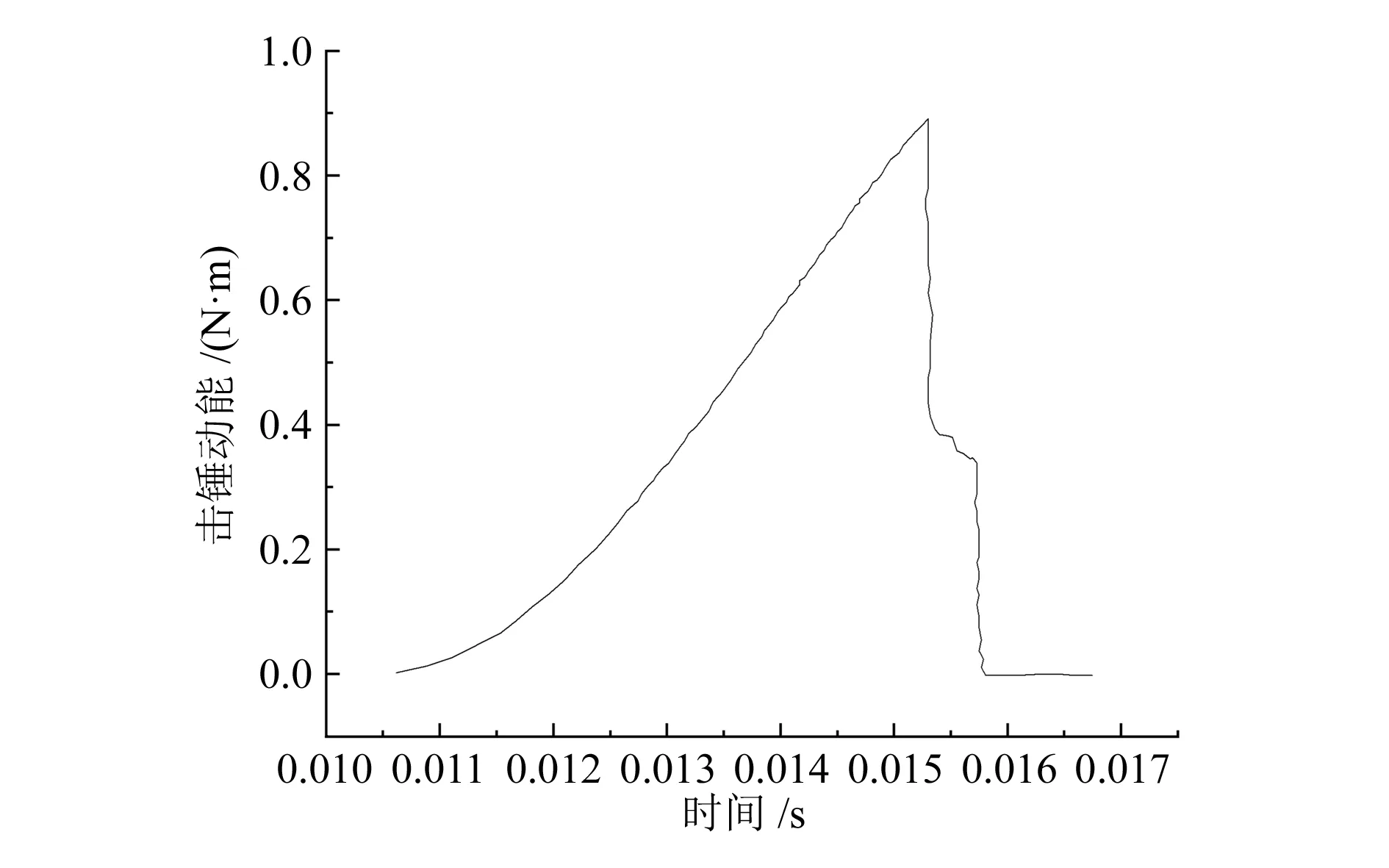
图5 击锤动能变化曲线

图6 击针动能变化曲线

在表1中的误差区间内,对不确定输入参数进行采样,选取300组数据作为采样点进行击发机构仿真计算。通过优化分析,得到章节2.2中的目标函数在优化迭代中的变化,如图7所示。从图7可知,仿真采用不同的优化方法,目标函数收敛的速度不同,全局优化阶段目标函数收敛比较慢,梯度优化阶段收敛比较快。

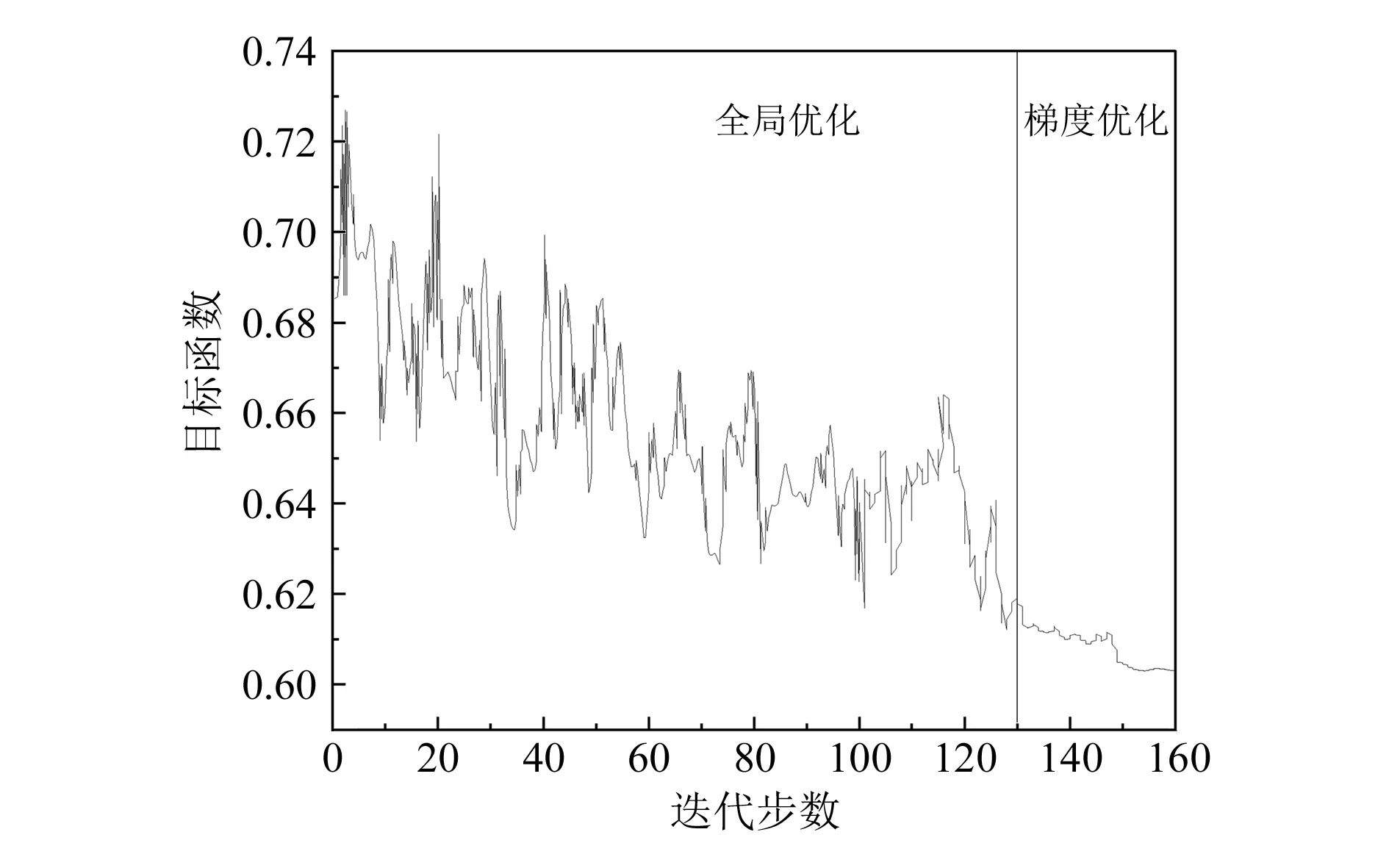
图7 目标函数随优化迭代步数变化

该击发机构为击锤回转式击发机构。击发过程的实质是击锤撞击击针,击针撞击底火,底火壳发生变形。

本文提出用底火壳的变形能计算击发能量,分析仿真计算结果可知,击发机构的底火能在优化后减小,优化后的底火能比优化前降低了17%,并且能够保证击发机构100%击发,图8所示为底火能优化前后的变形能曲线对比,说明击发机构的结构优化对击发性能的提高有明显效果。

图8 优化前后变形能曲线

4 结论

本文阐述了击发机构的工作原理,将击发机构中的变量分为非随机变化与随机变化的设计变量,在此基础上,建立了某自动步枪击发机构动力学模型与优化模型。采用全局与梯度优化组合算法对击发机构进行优化。得到如下主要结论:1)将底火变形能作为优化目标函数,优化设计更符合实际情况;2)所提的优化方法能有效用于发射机构的优化设计,为击发机构的设计提供了一种可靠方法。