基于滑模内模控制的珩磨恒速进给系统控制研究

王 双,龚 俊,李奇军

(1.兰州理工大学数字制造技术与应用省部共建教育局重点实验室,甘肃 兰州 730050) (2.兰州理工大学机电工程学院,甘肃 兰州 730050)

随着工业自动化水平的逐步提高,永磁同步电机也越来越多地被应用于珩磨机床[1-2]。在珩磨油石进给系统中,传统的PI控制策略下的系统存在参数波动大、尺寸精度差等问题[3-5],因此应使用一些先进的控制策略来满足进给系统的高性能要求。Han等[6]提出了一种滑模观测器,并采用自适应方法解决对电机参数变化敏感的问题;刘巍等[7]基于内模控制原理设计重复控制器,有效减小了速度的波动,提高了系统的抗干扰能力;田乐乐等[8]设计了模糊滑模速度控制器和内模PI电流控制器,不仅抑制了滑模抖振,还提高了系统的调节速度。为了解决传统PI控制策略下珩磨系统存在的不足[9],本文在恒速进给系统中提出滑模内模控制方案,设计滑模控制器和内模控制器,搭建模型参考自适应的进给系统仿真模型,并对仿真结果和实验结果进行对比分析,结果表明,基于滑模内模的控制方法比基于传统PI控制方法的响应时间更短,稳定性更好,工作效率更高,更能满足油石恒速进给的条件。

1 控制方案与控制器设计

为了使系统具有更快的响应速度和更高的尺寸精度,设计基于滑模内模控制模型参考自适应控制方案,将设计的滑模速度控制器加至控制系统的转速环中,内模控制器加至转速环和电流环的信号反馈系统中。基于滑模内模控制的模型参考自适应控制系统框图如图1所示。

图1 基于滑模内模控制的模型参考自适应控制系统框图

1.1 滑模速度控制器设计

在电机驱动珩磨恒速进给系统中,为了提高系统动态响应速度,减小系统中存在的抖振和误差,需要根据滑模速度控制原理,对滑模速度控制器进行设计。

定义PMSM(永磁同步电机)系统的状态变量:

(1)

式中:x1、x2为PMSM系统的状态变量;wref为电机的参考转速,通常为常量;wm为电机的实际转速。

根据电机数学模型和系统状态变量可得:

(2)

(3)

定义滑模面函数:

s=cx1+x2

(4)

式中:s为滑模面;c>0,为待设计参数。

对式(4)求导,可得:

(5)

为了使电机驱动系统具有较好的动态品质,采用指数趋近律方法,可得:

(6)

(7)

式中:ε为系统的运动点趋近滑模面s=0时的速率,ε>0;ks为指数趋近项,且k>0。

1.2 内模控制器设计

为了对电流环 PI 控制器进行参数整定,实现对交叉耦合电动势的完全解耦,需要在内模控制算法的基础上,对内模控制器进行设计。

采用常规的PI调节器并结合前馈解耦控制策略,可得d-q轴的电压为:

(8)

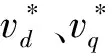
为了使系统完全解耦,在此基础上设计内模控制器,如图2所示。

图2 内模控制结构图

(9)

式中:I为单位矩阵,C(s)为内模控制器。

(10)

将式(10)代入式(9)可得:

(11)

式中:R为定子电阻。

通过分析,可得PI的整定值为:

Kpd=αLd,Kid=αR,Kpq=αLq,Kiq=αR

(12)

2 仿真建模

本文通过分析珩磨进给系统结构,将对油石的恒速进给控制转换为对电机的恒转速控制,利用MATLAB/Simulink软件建立基于滑模内模控制策略的系统仿真模型,如图3所示,系统仿真参数见表1。已知齿轮传递效率[10]为η1=0.976,将表中参数代入公式η2=Ph/(Ph+0.02dh)中,计算可得滚珠丝杠传动效率η2=0.992 6。

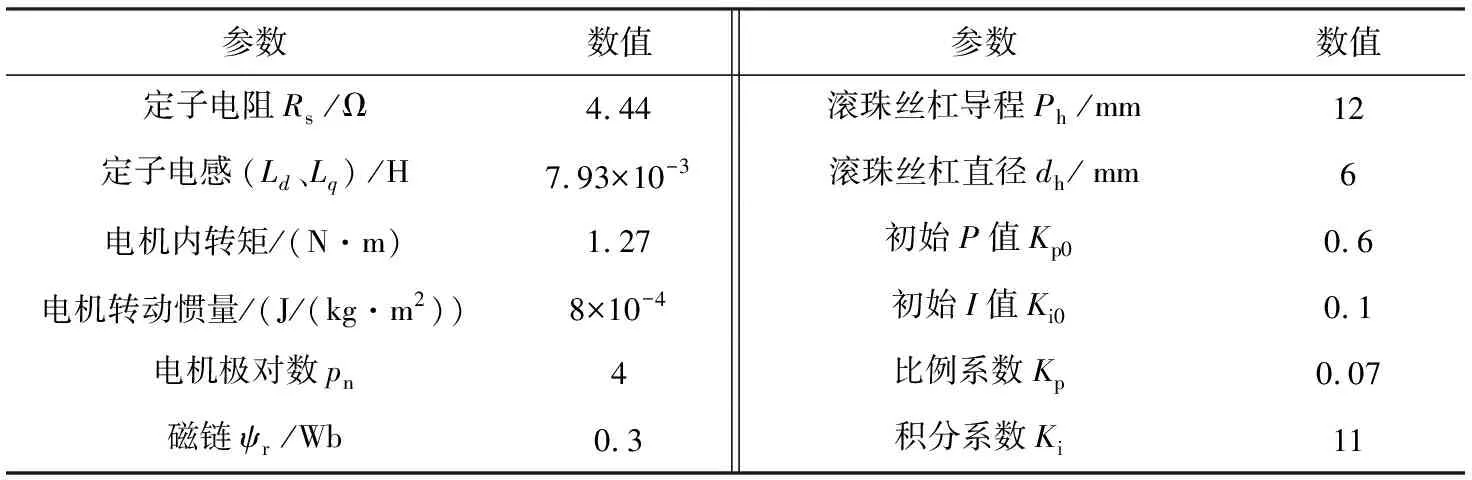
表1 系统仿真参数

图3 基于滑模内模控制的系统仿真模型

3 实验验证与对比分析

3.1 实验平台搭建

实验平台所选用的永磁同步电机型号为80ST-M01330,其参数值见表1。平台包括永磁同步电机、三相电机驱动板、数字信号处理器(DSP)、DSP仿真器、隔离变压器、控制开关、电源和笔记本电脑等器材。实验平台实物如图4所示。

图4 实验平台实物

3.2 仿真结果和实验结果对比分析

由仿真模型及实验平台可以得到不同控制策略下系统的仿真结果和实验结果,对其进行对比分析,以验证仿真模型的可行性和仿真结果的正确性。

1)不同控制策略下负载正向时仿真和实验结果对比分析。

设定电机转速为1 000 r/min,运行时间0.7 s,0—0.2 s为空载,在0.2 s和0.5 s时负载力矩为300 N ·m和700 N·m,基于滑模内模控制方法与传统PI控制方法的仿真和实验结果对比如图5和表2所示。

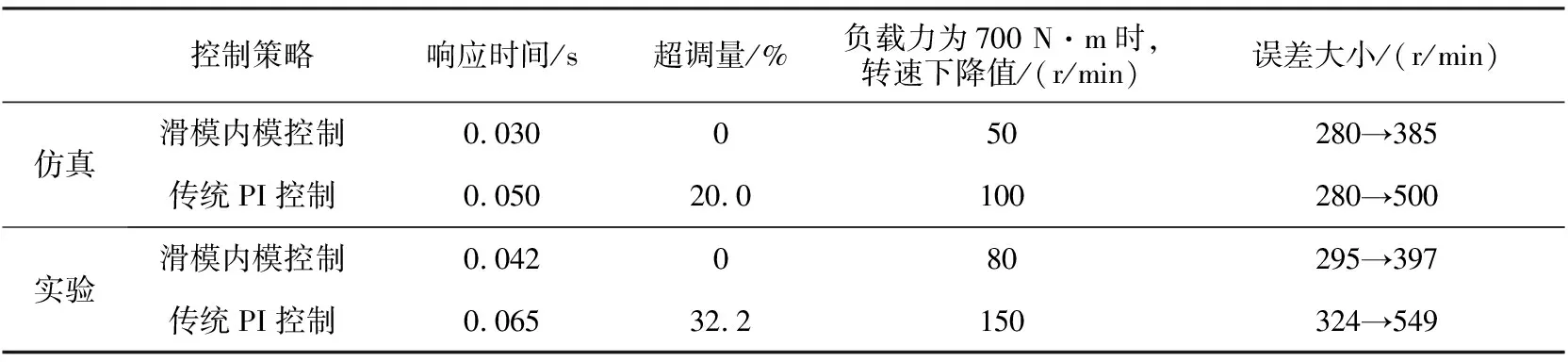
表2 不同控制策略下负载正向时仿真和实验结果对比

由图5和表2可知,当负载正向时,无论是仿真还是实验,速度和误差响应曲线趋势是一致的,只有微小的误差,波动幅值均随着负载的增大而增大,但基于滑模内模控制策略下的系统比基于传统PI控制策略下的系统响应速度快,且没有超调量,转速波动较小,转速误差也较小。在实验过程中,因各种不确定因素的干扰,各参数值偏大。故在珩磨进给系统中,选用滑模内模控制更能获得较好的工件表面质量和更高的尺寸精度。

2)不同控制策略下负载反向时仿真和实验结果对比分析。

设定电机转速为1 000 r/min,运行时间0.7 s,0—0.2 s为空载,在0.2 s和0.5 s时负载力矩为-300 N·m和-700 N·m。基于滑模内模控制方法与传统PI控制方法的仿真和实验结果对比如图6和表3所示。

表3 不同控制策略下负载反向时仿真和实验结果对比

图6 不同控制策略下负载反向时仿真和实验结果对比

由图6和表3可知,当负载反向时,仿真和实验中基于滑模内模控制策略下的系统比基于传统PI控制策略下的系统响应速度快,且没有超调量,速度和误差响应趋势较稳定且波动较小,误差也较小。实验过程中,由于各类因素的影响,系统中各参数值均有所增大,但无论是仿真还是实验,响应趋势曲线是一致的,只有微小的误差,且负载越大,波动幅值均越小。而传统PI控制策略下的转速和误差响应随着反向负载的增大变得不稳定,需要较长的时间才能恢复,因此在珩磨进给系统中选用滑模内模控制更容易得到满足工程应用要求的加工工件。

4 结束语

本文通过简化珩磨进给系统结构,将对珩磨恒速进给控制转换为对电机的恒定转速控制,设计了滑模控制器和内模控制器,减小转矩波动和转速误差,提高了珩磨加工质量和工件尺寸精度。通过对比分析不同负载方向的两种控制策略下的仿真结果和实验数据,表明基于滑模内模控制策略下的控制系统具有比传统PI控制策略下的系统响应速度快、波动小、误差小和鲁棒性强等优点,同时也验证了仿真结果的真实性和可靠性。但由于实验中不可控因素的影响,实验结果与仿真结果有微小误差。