基于轴承回转精度预测的轴承元件选配优化

杜同成,邱 俊,毛范海

(大连理工大学机械工程学院, 辽宁 大连 116024)

轴承合套是轴承装配中的一道重要工序,套圈及滚动体的选配对轴承装配精度和回转精度有着决定性影响。关于轴承回转精度的研究,章一强[1]结合瞬态热网络方法构建轴承热力耦合动力学模型,并从轴承结构设计角度分析了轴承工况条件和结构参数对轴承旋转精度的影响规律;Okamoto等[2]通过数值计算和实验方法,研究了轴承外圈形状误差和滚动体直径误差及数量与轴心轨迹的关系,并给出了影响规律;Noguchi等[3]建立了两自由度力学模型,研究了波纹度和滚动体直径误差对轴承径向跳动的影响规律;余永健等[4]提出了考虑内圈滚道、外圈滚道和滚动体表面几何误差的圆柱滚子轴承旋转精度数值模型;李传顺、吴柏华等[5-6]根据深沟球轴承元件运动几何关系建立数学模型,分析了深沟球轴承内外圈滚道圆度误差、滚动体直径误差及排布方式对轴承跳动的影响规律。关于轴承选配的研究,柳枫[7]通过选配合适的径向游隙,对深沟球轴承和角接触球轴承装配工艺进行改进,实现了轴承的分组互换或全互换合套;张娟[8]分析了影响径向游隙的因素,提出了合理有效的方法改进深沟球轴承的径向游隙以提高合套质量;陈国金等[9]提出一种新的迭代算法,对分档匹配完成后的内外圈进行二次匹配,得到具有最佳初始游隙的合套轴承。

关于轴承回转精度的研究已经取得了丰硕的成果,而在轴承选配方面,主要还是通过分组选配和以最佳游隙为目标进行选配,一定程度上忽略了轴承回转精度。针对以上现存问题,本文提出了可以进行轴承回转精度预测的轴承元件选配优化方法,利用现有的轴承内圈、外圈和滚动体进行分组优化匹配,以提高轴承的合套率以及回转精度。

1 轴承回转精度数值模型

1.1 模型假设

建立轴承外圈固定、内圈低速旋转状态下考虑轴承元件几何误差的深沟球轴承回转精度数值模型。模型建立过程中作以下假设:1)针对小尺寸轴承,忽略内圈的偏摆;2)采用刚性套圈,滚动体只作纯滚动;3)滚动体仅存在直径尺寸误差,同一轴承的所有滚动体大小一致;4)不考虑保持架、套圈挡边的影响;5)不考虑弹流润滑条件。

1.2 初始模型

如图1所示,以轴承外圈沟底最小二乘圆圆心为原点建立固定坐标系O-XYZ,以轴承内圈沟底最小二乘圆圆心为原点建立运动坐标系O-XrYrZr,在初始状态下,两坐标系重合,取轴承轴向截面建立坐标系O-Xer,简化为平面坐标系。其中φ为滚动体位置角,r为滚道曲率半径,ΔRi,j为内圈滚道在第j个滚动体处的轮廓幅值,ΔRo,j为外圈滚道在第j个滚动体处的轮廓幅值,Dr为滚动体理论直径,Dw,j为滚动体j实际直径,Oi为内圈沟曲率中心,Ob为滚动体中心,Oo为外圈沟曲率中心。

初始状态下,内、外圈沟曲率中心距第j个滚动体中心的距离Li,j和Lo,j分别为:

(1)

式中:ri、ro分别为内、外滚道曲率半径,gi,j和go,j分别为第j个滚动体处内、外圈滚道与滚动体的实际间隙。其计算公式如下:

(2)

式中:ur为实际径向游隙。

滚道截面轮廓用一条周期性变化的封闭曲线来描述,可由傅里叶级数展开,则圆度误差函数如下:

(3)

式中:akq、bkq(q=i,o,i表示内圈,o表示外圈)为套圈圆度误差函数傅里叶展开式的系数;φj为第j个滚动体的位置角;θ为内圈转过的角度,θ=ωit,t为内圈转动时间,ωi为内圈旋转角速度;m、n分别为两个函数的收敛级数。

当内圈转过的角度为θ,则在固定坐标系XOY象限中,滚动体的位置角φj为:

(4)

式中:φ0为第一个滚动体位置的初始角度;Di为理论内圈滚道直径;j=1,2,…,N,N为滚动体个数。

初始状态下,滚动体j处内、外圈沟道曲率中心在固定坐标系下的坐标(xq,j,yq,j,zq,j)为:

(5)

式中:dm为轴承平均直径。式中“±”,内圈取正,外圈取负。

过坐标系O-Xer中的坐标轴er和固定坐标系中的Z轴建立坐标系O-Zer,则滚动体j处内、外圈沟道曲率中心在er-z平面内的坐标为:

(6)

1.3 受载模型

受载状态下,内圈出现偏移时,运动坐标系相对于固定坐标系在X、Y、Z方向分别产生Δx、Δy、Δz的位移,如图2所示。由于内圈的偏移,滚动体将沿外圈滚道向内圈轴向位移方向移动,因此接触角αj发生改变,如图3所示。

图2 运动坐标系相对固定坐标系偏移

图3 内外圈相对位置

(7)

在er-z平面内的坐标为:

(8)

第j个滚动体处的接触角αj的正、余弦函数分别为:

(9)

其中内圈与外圈沟道曲率中心的距离Δj为:

(10)

1.4 力学模型

在内圈上施加一个很小的稳定轴向力Fz,则每个滚动体与滚道的法向接触载荷Qj为:

(11)

式中:δj为滚动体j处的弹性变形量,Kn为滚动体与内外圈之间总的负荷-变形常数。Kn与Ki、Ko的关系如下:

(12)

式中:Ki、Ko为滚动体与内、外圈之间的负荷-变形常数。滚动体受载后产生变形,轴承内外圈滚道与滚动体接触点的弹性变形关系如图4所示。

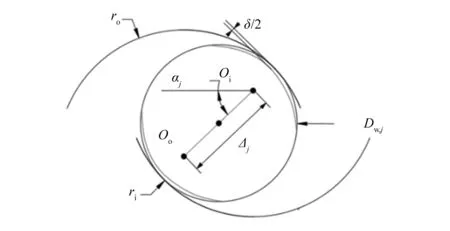
图4 接触点处弹性变形

根据图4所示变形几何关系,第j个滚动体与滚道接触后产生的弹性变形δj为:

δj=Dwj-(ri+ro-Δj)

(13)

若δj> 0,则该位置处滚动体与滚道发生弹性变形,Qj> 0;否则不受载,Qj= 0。则受力平衡方程为:

(14)

式中:Fx、Fy分别为内圈所受径向力在X和Y方向的分力,Fa为内圈所受的轴向力。

利用Newton-Raphson迭代求解数值模型,得到内圈旋转一周时不同角度的位移,则轴承内圈的径向跳动量Δr和轴向跳动量Δa为:

(15)

式中:Δx、Δy、Δz分别为轴承内圈在x、y、z方向的位移。

2 轴承元件匹配优化

在一批轴承零件中随机选取10个外圈,编号为k,10个内圈,编号为i,按照滚动体实际直径与理想值的偏差,将在一定偏差范围内的滚动体分到一组内,共分为10组,编号为j,其中i,j,k= 1,2,…,10,以此为基础进行轴承零件的分选并进行轴承合套,每匹配成功一次,重新补进一个内圈和外圈。

文中根据不同的约束条件建立两种分选方案,第一种以满足游隙及精度要求为条件进行分选;第二种以满足游隙要求且跳动量最小为约束条件进行分选。图5为轴承元件选配方案流程图。

图5 轴承元件选配方案流程图

分别选择一个内圈、外圈及滚动体进行组合,代入零件结构尺寸,按照式(16)求解轴承径向游隙ur:

ur=do,k-di,i-2Dw,j,i,j,k=1,2,…,10

(16)

式中:do,k为外圈沟道真实直径,di,i为内圈沟道真实直径。

当前组合满足游隙要求时,即μrmin≤μr≤μrmax,其中μrmax、μrmin分别为标准精度等级要求的最大、最小轴承径向游隙,将零件尺寸等数据代入回转精度数值模型计算得到轴承内圈径向跳动和轴向跳动,然后根据式(17)求解轴承综合跳动量Δ。

(17)

3 算例分析

选取某公司提供的型号6312深沟球轴承,取50个外圈与50个内圈,并按照标准GB 308—2002,以1 μm的公差将滚动体分为10组。为了对比分析,方案1为随机匹配各轴承元件,不作任何条件约束;方案2为针对文中提出的选配方案,根据标准GB/T 307.1—2017,以精度为P5等级轴承的跳动量公差(径向跳动为5 μm,轴向跳动为8 μm)设置约束条件,具体见表1。

表1 约束条件 单位:μm

输入表2中的参数和轴承零件编号(根据零件编号代入对应尺寸参数数据)进行分选。

表2 输入参数

分别按照本文提出的两种轴承元件选配方案以及传统轴承元件装配方法进行轴承装配,得到40组成套轴承的径向跳动量和轴向跳动量以及径向游隙,不合格数量及跳动量均值见表3。

表3 轴承不合格数量及跳动量均值

按照传统方法进行轴承元件装配,得到轴承的径向跳动量和轴向跳动量如图6所示。参与计算的所有轴承的平均径向跳动量为1.19 μm,平均轴向跳动量为4.64 μm,其中有22.5%的轴承轴向跳动量超过了8 μm,不符合回转精度要求。

图6 轴承元件随机匹配的跳动量

按照方案1(满足游隙及精度要求)进行轴承元件装配,得到轴承的径向跳动量和轴向跳动量如图7所示。参与计算的所有轴承的平均径向跳动量为1.06 μm,平均轴向跳动量为3.14 μm,其轴承轴向跳动量和径向跳动量均在要求范围内,表明对轴承元件进行合理选配可以提高轴承的回转精度及合套率。

图7 满足游隙及精度要求匹配的跳动量

按照方案2(满足游隙要求且精度最优)进行轴承元件装配,得到轴承的径向跳动量和轴向跳动量如图8所示,参与计算的所有轴承的平均径向跳动量为1.01 μm,平均轴向跳动量为2.42 μm,且轴承轴向跳动量和径向跳动量均在要求范围内。相比前两种选配方案,该方案得到的轴承精度更高。

图8 满足游隙且精度最优匹配的跳动量

图9所示为按照三种轴承装配方案进行轴承装配得到的轴承径向游隙。结果显示,按照传统方法装配,有27.5%的轴承的径向游隙超过了43 μm,而按照本文方案,轴承的游隙均在要求范围内,说明本文方案可有效提高轴承的合套率。

图9 三种方案所得轴承游隙对比

将三种方案得到的轴承综合跳动量以升序的方式排列,进行对比,结果如图10所示。由图可知,传统方法得到的最大轴承综合跳动量为14.82 μm,方案1得到的最大轴承综合跳动量为7.82 μm,方案2得到的最大轴承综合跳动量为7.53 μm。相比传统装配方法,文中提出的两种选配方案均可有效提高轴承的回转性能。但使用方案2得到的内圈跳动量更小,合套轴承回转精度更高。

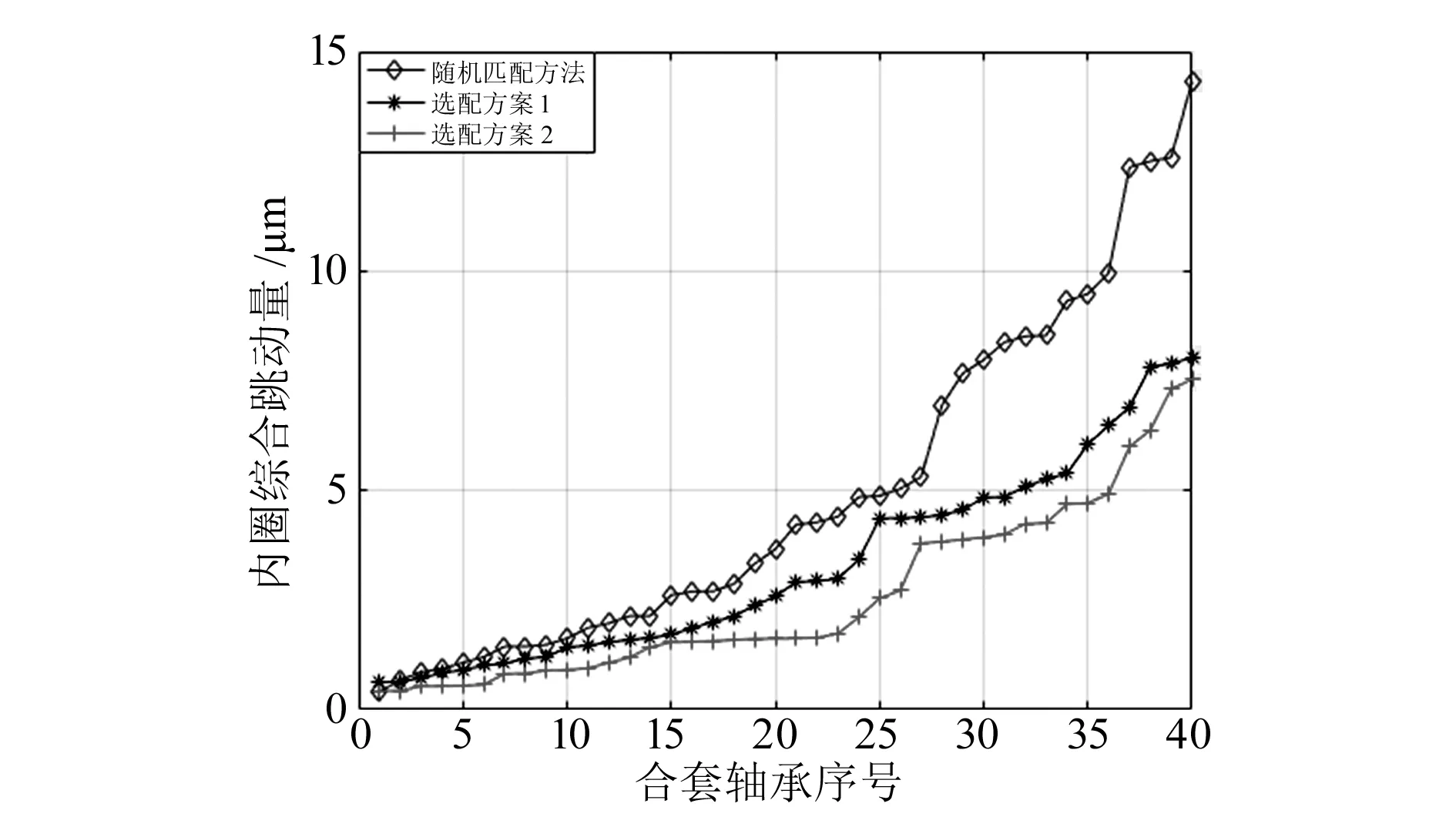
图10 三种方案所得综合跳动量对比

4 结束语

本文通过对轴承元件几何误差与轴承回转精度间的关系研究,发现根据轴承元件几何误差进行合理的组配,可以有效提高轴承合套率及回转精度。实际生产中可以通过提高元件加工精度的方式,提高最终成套轴承的回转精度。