基于改进PID的机器人机械臂控制器设计

黄烨东,吴晨曦

(中国石油大学(北京)机械与储运工程学院,北京 102249)

随着工业自动化的不断发展,自动化作业逐渐代替人工操作。在机械运动中,不同轨迹规划会产生不同程度的振荡以及能耗[1-3]。机器人是典型的机电一体化设备,在制造业、农业、医疗、海洋工程等领域都有十分广泛的应用[4-7]。在医疗领域,机器人开始辅助医师进行高精度、步骤复杂的外科手术,因此机器人机械臂移动需要保证优良的稳定性与速度[8-10]。为此,本文利用李普诺夫非线性大范围渐近稳定原理对定位方程进行求解,然后采用自整定模糊比例-积分-微分(PID)控制和脉宽调速(pulse width modulation,PWM)相结合的方式,对机械臂的移动行为进行控制,为各项高精度的机械工作提供技术保障。本文研究的创新点有以下3个方面:传统的数值计算方法对每次移动定位产生的误差并不能及时校正,且计算量大,为此基于李雅普诺夫非线性大范围渐近稳定原理对非线性运动方程进行求解,同时利用偏差反馈系数对求解过程进行优化;将自整定模糊控制PID方式与PWM控制相结合,实现高精度与高稳定性的机械臂运动控制;在对机械臂进行控制的同时,实现了空间路径的规划。

1 基于自整定模糊PID控制与PWM控制的机械臂控制器设计与实现

1.1 基于李雅普诺夫非线性大范围渐近稳定原理的机械臂空间运动路径规划

对机器人机械臂的运动空间轨迹进行规划,首先求出其末端执行器所对应的关节变量值,根据逆运动学方程对各路径点的末端执行器所对应的关节变量值进行计算,然后拟合出相应的运动过程函数。一般采用Denavit-Hartenborg(D-H)法则对机器人的每个机械臂支臂进行表征。以外科手术机器人机械臂为原型进行仿真,机械臂共有3个关节,分别为肩部、肘部和腕部关节,基于D-H表示的机械臂运动学模型如图1所示。图中,相邻的机械臂支臂可以近似为保持相邻关节之间相对位置的刚体。第一个支臂为i,第n个支臂为(i+n),采用4个参数对机器人的每个支臂进行描述,分别为支臂长度di、支臂扭角θi、支臂偏距ai以及关节转角αi。

图1 基于D-H表示的机械臂运动学模型

首先建立支臂的参考坐标系,针对具有3个关节的机械臂建立3个关节点的局部坐标系。z轴上的3个关节点参数下标分别为i-1、i、i+1,从而可确定支臂坐标系中所有轴的位置,得到相应的参考坐标系。当前坐标系通过四次齐次变换可得4个机械支臂的单个D-H变换矩阵,矩阵变换方法如式(1)所示:

Ai=Rot(z,θi)Trans(0,0,di)Trans(ai,0,

0)Rot(x,αi)

(1)

式中:Ai为变换矩阵,Rot(z,θi)为D-H变换矩阵绕z轴旋转角度θi的操作,Trans(ai,0,0)和Trans(0,0,di)为沿轴移动操作,Rot(x,αi)为D-H变换矩阵绕x轴旋转角度αi的操作。通过旋转和平移操作,实现了当前坐标系与参考坐标系原点的重合。最终得到的变换矩阵Ai如下:

(2)

得到单个变换矩阵之后,需要对每个机械支臂的矩阵进行整合,得到整个机械臂的运动方程:

A=A1A2A3…Ai

(3)

式中:A为所有机械臂末端支臂相对于整个坐标系的位姿矩阵方程,即机械臂的运动学方程。机械臂移动的最终目标点坐标(x3,y3,z3)与各支臂相关关节角θ之间的关系如下:

(4)

式中:R1、R2、R3分别为3个关节末端的点坐标,θ1、θ2、θ3分别为3个关节的支臂扭角。在研究过程中发现,传统的数值计算方法对运动方程进行求解结果并不理想,误差不能够及时校正,且计算量大,计算时间长。为了简化计算,快速求得唯一的合理解,本文基于李雅普诺夫非线性大范围渐近稳定原理对非线性运动方程进行求解。为消除实时控制中出现的位置偏差,根据机械臂当前状态和目标位置,利用偏差反馈系数对移动距离进行校正。对每一次出现的位置偏差进行角度修正的计算方法如下:

(5)

(6)

(7)

式中:f(θ)为非线性方程组,f′(θ)为非线性运动方程的矩阵表示形式,J(θ)、Q(θ)和V(θ)分别为雅可比矩阵、正定矩阵和李雅普诺夫矩阵,P为加权后的正定矩阵。当|θ|趋近于无穷、V(θ)趋近于无穷时,系统空间原点θe=0的平衡状态为李普诺夫非线性大范围渐近稳定状态。利用式(7),在保证Q(θ)为正定矩阵的情况下对偏差反馈系数进行调整,从而在保证精度的情况下实现更加快速的移动。通过偏差反馈系数的不断调整,直到误差阈值ε达到理想状态停止校正。误差阈值ε计算公式为:

(8)

式中:k为机械臂实际要求精度,结合实际应用,k值设置为0.1 mm。

综上,本文构建了一种多关节机械臂非线性定位方程,利用李雅普诺夫非线性大范围渐近稳定原理对定位方程进行了计算。

1.2 基于改进PID控制的机械臂控制方法

为实现较为灵活的操作,在每个关节中安插了两个电机。机械臂在运动过程中一般很难兼顾稳定性与移动速度,而常规PID控制中需要通过调节参数使系统响应,因此系统是否能够得到优良的控制效果与参数调整有着紧密联系。为保证系统在环境不断变化的情况下尽快寻找到最优的参数组合,采用模糊控制器对PID控制进行参数自整定,实现较为快速、稳定的机械臂操控。为提高机械臂操作的稳定性,利用自整定模糊PID控制对机械臂各关节进行控制。电机模糊控制是基于模糊集理论和模糊逻辑推理的一种可运用于计算机的控制方式。电机模糊控制示意如图2所示。

机械臂运动过程中,想要保证机器人整体协同操作,必须对启动速度与运动速度进行实时控制。为此对机器人的工作空间进行划分,对划分后的子空间进行模糊PID控制,这样可保证机械臂整体与局部的速度皆在设计要求范围内变化。利用模糊理论对参数进行整定,控制器根据每次反馈的系统偏差以及偏差的变化概率,通过查询模糊控制表对相应参数进行调整,然后进行PID运算。当机械臂的相关关节控制系统半开时,采用重心法进行逆模糊化处理。处理方法如下:

(9)

式中:Kp、Ki和Kd分别为比例、积分、微分调节系数,Kp、Ki和Kd的数值经过模糊控制规则表求得;T为控制时间;e(k′)为k′采样周期的偏差值;μ(k′)为k′采样周期的输出;k′为采样周期序号;e(j)为j采样周期的偏差值,j的取值范围为[1,k′];Δe(k′)为对偏差和时间进行求导的最终结果;Kμ为比例因子;μ为最终的精确输出量。当机械臂离目标点位置较远时,控制器首先确定需要到达的点所在子空间的隶属度函数,然后根据该函数选定所在的模糊区域,在机械臂移动至模糊区域后进行位置的精确校正。为防止电机在机械臂移动过程中出现多余的抖动,使用PWM对输出电压进行控制。利用微处理器的数字输出对模拟电路进行控制,保持输出电压值的稳定性。PWM信号可以生成一个数字信号,在达到置零时间时对信号置零。此时PWM信号占空比γ为:

(10)

式中:T′为信号置零时间,t′为脉冲时间。使用LabVIEW程序对PWM信号进行控制,PWM信号的简易实现方式如图3所示。

图3 LabVIEW程序中PWM信号的简易实现方式

机械臂关节点位置的确定与脉冲数、标定表电压联系紧密。为保证电机稳定,不出现多余振动影响机械臂的定位,需要通过调节脉冲大小来降低其旋转速度。当机械臂定位误差出现较大偏差时,采用脉宽较大的脉冲。当机械臂定位误差偏差较小不用调节时,控制系统关闭,此时采用窄脉冲。通过不断改变脉冲宽度,使关节能够平稳到达目标位置。利用PWM控制能够较大程度降低系统所需的电力成本以及功率消耗。脉冲数n的计算公式为:

n=ζf(θ)

(11)

式中:ζ为线性系数。PWM控制过程中脉冲数量确定之后,机械臂移动到目标点附近。根据角度传感器反馈确定机械臂的角度位置,并做负反馈校正。如果机械臂仍未到达正确位置,通过正向与负向的脉冲反馈,调整机械臂末端坐标,直到与目标点距离处于阈值范围内结束移动。

2 基于改进PID的机器人手臂控制器性能分析

本文通过将PWM控制与自整定模糊PID控制相结合实现机械臂控制器的设计。在LabVIEW中进行模拟仿真,选取机器人运动空间的移动点位进行运动位置精度的测量。采用POLARIS光学导航仪作为测量工具,设计了一系列实验对控制算法进行性能分析。为检验本文设计的基于李普诺夫非线性大范围渐近稳定原理对机械臂非线性定位方程求解方法在机械臂定位中的应用效果,将传统数值运算方法与所设计的非线性定位方程求解方法进行模拟仿真。设置4个长度不同的机械臂,在空间内对同一组目标点进行定位计算。在同一时间内,利用上述两种方法对目标点进行跟踪,并记录其关节角误差变化情况。实验中采样点的步长为0.002 s,相应变化曲线如图4所示。

由图可知,机械臂在运动过程中,可能会在接近目标点的周围产生扰动,且随着机械臂杆长R增加,角度误差变化幅度加大。其中本文设计方法的角度误差平均变化范围为±1.2°,而传统数值运算方法为±2.8°。由此可知,本文设计方法具有更为优良的定位精度与实时运算能力。为实现更精确稳定的PID控制,将模糊理论与PWM控制相结合对PID进行优化改进。为检验改进PID控制算法的抑振效果,在仿真软件中进行振动控制模拟试验。在电机频率分别为1 Hz和10 Hz两种情况下,将两种算法的控制结果与无控制情况下的弹性变形曲线进行对比,具体如图5所示。

图5 改进前后控制算法弹性变形量变化曲线

图5(a)中,弹性变形量的峰值降低到了进行抑振控制前的27.68%;图5(b)中,弹性变形量的峰值降低到了进行抑振控制前的23.68%。两种驱动频率下,弹性变形得到相似的抑制效果。改进后算法的变化曲线振动幅度在约第2.9 s时基本趋于平稳,此时弹性变形得到了有效抑制。与PID控制相比,系统振荡得到了有效抑制,稳态精度得到显著提高。为进一步验证PWM控制与自整定模糊PID控制相结合的控制算法(算法1)的控制性能,将该算法与其他目前流行的机械臂控制算法进行对比实验。对比算法包括基于层次深度强化学习的机械臂控制算法(算法2)、基于神经网络和模糊补偿的机械臂控制算法(算法3)、基于姿态枚举算法的机械臂控制算法(算法4)、基于改进差分进化算法的机械臂控制(算法5)。将5种算法在3个关节上的跟踪误差情况记录于图6中。

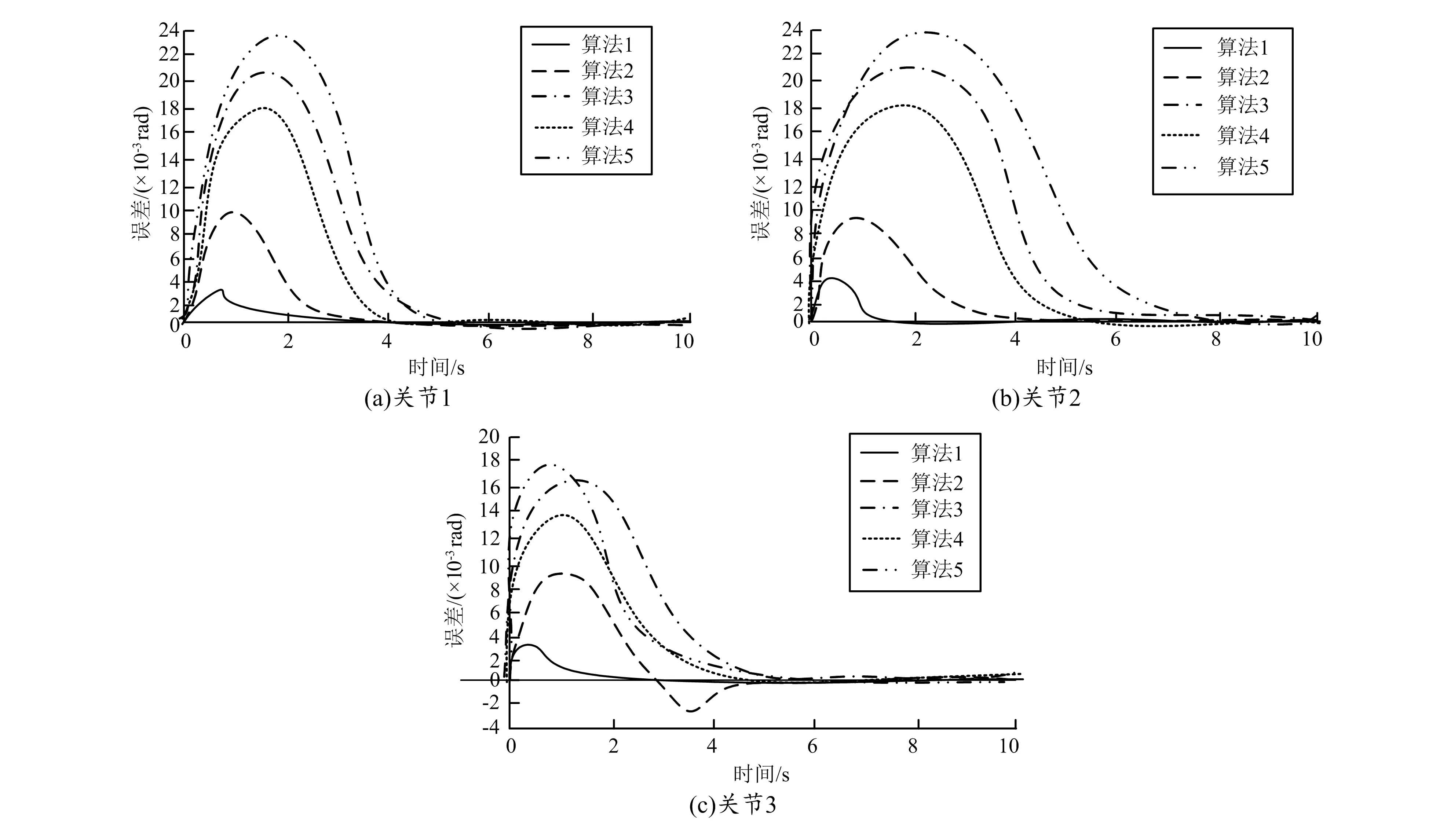
图6 3个关节中各算法控制下的跟踪误差情况对比

由图可知,5种控制算法的跟踪误差皆随着时间逐渐趋于稳定,保持在极小误差情况下。其中算法1趋于稳定所使用时间最短,在1.500 s左右基本实现精准控制,且最大误差小于4×10-3rad。另外4种控制算法趋于稳定所用时间与最大误差值皆大于算法1。由此可知,算法1能够在较快时间内实现机械臂的精确控制。为更全面对各算法性能进行比较,选取其中更具代表性的两个关节控制情况进行指标数值的记录。具体见表1。

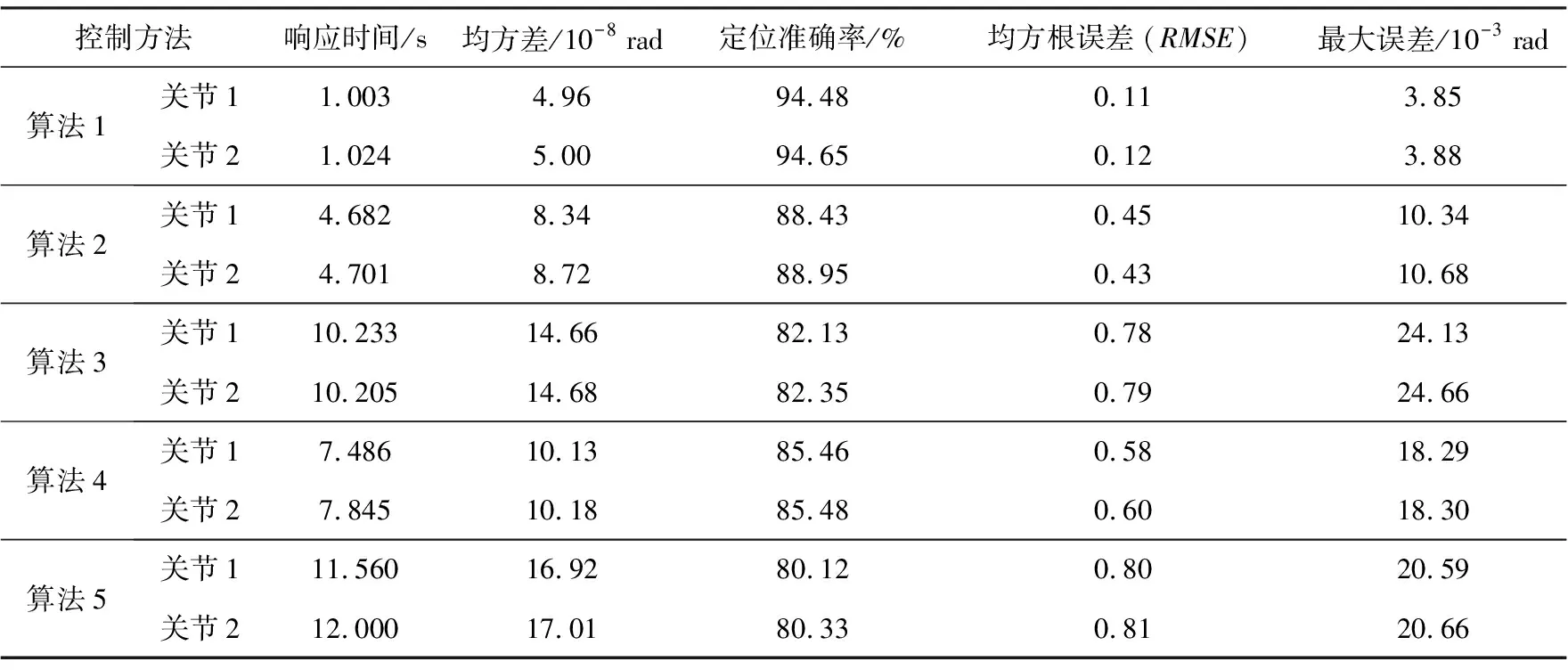
表1 各控制算法对机械臂各关节的角度跟踪情况分析

由表可知,算法1的最大定位误差值最小,响应最快,平均响应时间为1.014 s,平均均方差为4.98×10-8rad,平均定位准确率为94.57%,平均均方根误差RMSE值为0.11,平均最大平均误差值为3.87×10-3rad,明显优于另外4个算法。由此说明,算法1能够及时进行定位校正,实现更加精准的移动控制。

3 结束语

随着人工智能技术的不断发展,机器人机械臂空间移动中,对其移动速度、稳定性、精确性的要求越来越高。本文利用李普诺夫非线性大范围渐近稳定原理对定位方程进行求解,然后将自整定模糊控制PID方式与PWM控制相结合,对机械臂移动进行控制。通过实验分析可知,本文所设计的非线性定位方程计算方法最终得到的机械臂末端定位角度误差的变化范围为±1.5°,精度与移动速度都基本符合相关参数要求。改进PID控制算法的变化曲线振动幅度较小,在约第2.9 s时基本趋于平稳,此时系统振荡得到了有效抑制。算法的平均响应时间为1.014 s,响应时间较快,对于机械臂的定位准确率达到了94.57%,能够及时进行定位校正,实现更加精准的移动控制。在未来研究中,将考虑使用更高级的算法,使得控制精度更高。