核级工艺管道支撑跨距研究

徐宁 范正伟 周莹

（上海核工程研究设计院有限公司，上海 200233）

0.引言

本文以核电厂设计工作中应用较广泛的ASME 规范作为计算的准则，在大量管道计算的基础上对管道系统进行了简化建模，根据计算结果并结合ASME 规范第III 卷NF 的推荐跨距，给出了DN25 至DN500 管道对应1g、5g、10g 和15g4 种加速度的最大支撑跨距。依照此跨距准则布置的管道和支撑相对合理，更易满足规范对于管道自重、压力和地震的要求。在计算支撑跨距时，自重工况下考虑同时满足ASME 规范对管道应力和变形的要求；地震工况下满足规范对管道应力的要求。考虑地震加速度为1g、5g、10g、15g4 种情况，每种加速度计算得到的跨距均与满足自重应力要求得到的跨距、满足自重工况下管道变形要求得到的跨距进行比较，取其包络值作为对应的最大支撑跨距[1]。

1.不含集中质量的支撑跨距计算

1.1 计算模型

本文在计算最大支撑跨距时考虑自重和地震两种工况。采用的模型为两端简支梁，管道质量沿梁长度方向均匀分布，如图1 所示。将管道模型简化为两端简支，承受均布质量的梁模型，假设在支撑间距为L 时，梁上应力最大处达到管道最大许用应力，通过应力方程求解得到此间距即为最大支撑跨距。

图1 简化管道模型图

其中：R=管道外径，单位mm；r=管道内径，单位mm；w=线密度，单位kg/m；L=支撑跨距，单位mm。

1.2 自重工况对支撑跨距的要求

根据ASME 规范，压力和自重的影响必须满足公式：

其中：B1、B2为所考虑部件的一次应力指数，对于本文中所考虑的直管单元，B1=0.5，B2=1.0；P=管道设计压力；D0=管道外径，单位mm；tn=管道名义壁厚，单位mm；M=自重在横截面上的合力矩，单位N-mm；Z=管道的截面模量，单位mm3；Sallow=所考虑的载荷相应温度下的许用应力，单位MPa。

如图2 所示，距离一端x 处的力矩为M，支撑处：

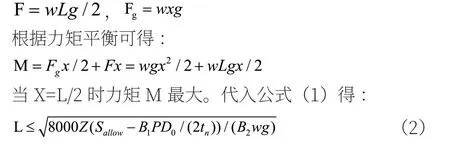
图2 简支梁受力示意图

1.3 地震工况对支撑跨距的要求

根据ASME 规范，对于压力、自重和地震载荷引起的应力必须满足公式：

其中符号同公式（1），只是：M=自重和地震载荷施加在管道横截面上的合成力矩，单位N-mm；保守考虑，地震加速度和重力加速度引起的弯矩使用绝对值相加的方式进行叠加。类似于1.2 节的推导过程，可得到支撑跨距为：

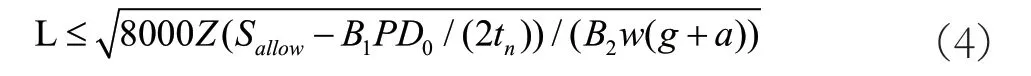
其中a 为最大地震加速度。

1.4 管道变形对支撑跨距的要求

ASME 规范NF-3600 给出了管道变形的要求，即管线的间隔能允许支撑间的管道有2.5mm 的下垂。对于简支梁，最大挠度和跨距有如下关系：

由此可得到：

表1 支撑跨距计算结果

2.含集中质量的支撑跨距计算

2.1 地震工况对支撑跨距的要求

当某个跨距内的管道上存在集中质量时，会对支撑跨距产生较为显著的影响。本节将集中质量及其偏心分解成作用在管道上的弯矩和扭矩两个分量，并依此来计算对支撑跨距的影响。为了进行计算，将1.1 节的计算模型做适当修改，其中一个支撑处增加扭转约束，管道上存在一个质量为m（单位kg），偏心距为d（单位mm）的集中质量，见图3。

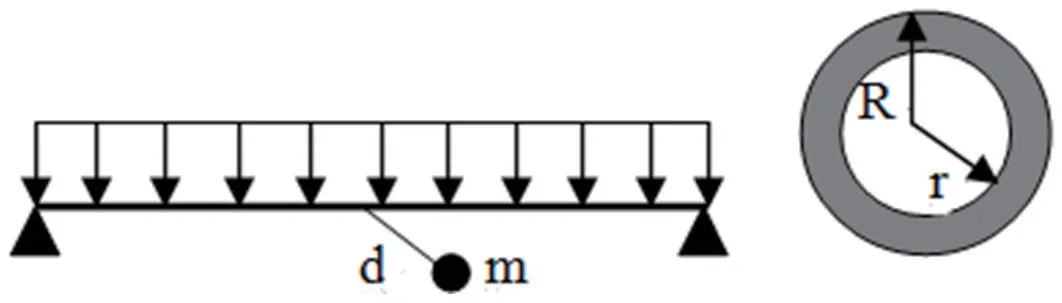
图3 含集中质量的简支梁受力示意图

集中质量和偏心在管道截面上产生弯矩和扭矩，类似1.2 节的推导过程，当集中质量在跨距的中间位置时在管道截面上产生的弯矩最大为：MB=maL/4+waL2/8；

最大扭矩为MT=m×a×d；

代入公式（3）可得到：

其中c=8000/(wa) ，Sp=PD0/(4tn)，lm=1000m/w

2.2 管道变形对支撑跨距的要求

当跨距中含有集中质量时，管道变形对跨距的要求也有所改变，集中质量位于跨距的中间时，产生的挠度最大，为：ymax=mgL3/(48 EI )

综合1.4 节的要求，由集中质量和管道均布质量共同引起的挠度不大于2.5mm，即：

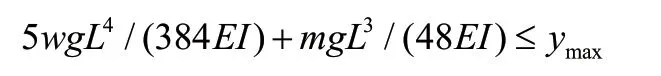
由此可近似得到：

2.3 计算结果

阀门是管道系统中常见的集中质量形式，本文总结了各管径下常见阀门的重量和偏心，代入公式（6）和（7）中可得到相应的最大支撑跨距，见表1。

3.结论

本文以管道满足ASME 规范对自重和地震的要求，通过计算得到了不同管径的管道对应的最大支撑跨距。依照此跨距布置的管道基本能够满足ASME 规范对管道自重、压力、和地震的要求，减少布置专业和力学专业之间的迭代次数；同时使各个支撑都能充分发挥作用，在保证管道系统满足设计要求的基础上尽量减少支撑数量，降低设计成本。