源于教材 挖掘应用
——三次方程根与系数的关系及应用探究
欧阳才学
(湖南省长沙市雅礼实验中学)
高中阶段,数学中经常出现一些与三次方程或三次函数有关的试题,求解“三次”问题的基本思路是“降次”,即通过配方、因式分解或换元等方法将“三次”降为“二次”,但解答过程往往比较繁琐.而对于许多“三次”问题而言,运用三次方程根与系数的关系解答,可简化计算.其实,三次方程根与系数的关系源于新教材的“阅读与思考”栏目,重视挖掘它的应用显得尤为必要.为此,本文首先给出一元三次方程根与系数的关系并予以证明,然后举例说明在解题中的应用.
一、三次方程的根与系数的关系
普通高中教科书人教A版数学必修第二册(2019年版)第82页给出了一元三次方程根与系数的关系,即韦达定理:
一元三次方程a3x3+a2x2+a1x+a0=0(a3≠0)的三个根分别为x1,x2,x3,则
【证明】因为x1,x2,x3是a3x3+a2x2+a1x+a0=0的三个根,
所以a3x3+a2x2+a1x+a0=a3(x-x1)(x-x2)(x-x3).
将右边展开,得a3(x-x1)(x-x2)(x-x3)=a3[x3-(x1+x2+x3)x2+(x1x2+x2x3+x3x1)x-x1x2x3]=a3x3-a3(x1+x2+x3)x2+a3(x1x2+x2x3+x3x1)x-a3x1x2x3,
所以a3x3+a2x2+a1x+a0=a3x3-a3(x1+x2+x3)x2+a3(x1x2+x2x3+x3x1)x-a3x1x2x3.
二、三次方程的根与系数关系的应用
应用1.求代数式的值
【例1】(2021全国高中数学联赛福建预赛)若x1=1,x2=1-i,x3=1+i(i为虚数单位)为方程x3+ax2+bx+c=0的三个解,则a+b-c=________.
【解析】根据三次方程根与系数的关系,得
解得a=-3,b=4,c=-2,
所以a+b-c=-3+4-(-2)=3.
【例2】(2023北京大学测试)设复数a,b,c满足a+b+c=a2+b2+c2=0,a3+b3+c3=3,则a2023+b2023+c2023的值为( )
A.0 B.3
C.2 023 D.其他三个选项均不对
【解析】因为(a+b+c)2=a2+b2+c2+2ab+2bc+2ca,
所以结合已知得ab+bc+ca=0.
又因为a3+b3+c3-3abc=(a+b+c)(a2+b2+c2-ab-bc-ca),
所以结合已知得abc=1.

所以根据三次方程的韦达定理可知a,b,c是方程x3-1=0的三个根.
因为2 023除以3的余数为1,所以a2023+b2023+c2023=a+b+c=0,故选A.
应用2.求解方程问题
【例3】(2020全国高中数学联赛浙江预赛)设r为方程x3-x+3=0的解,则以r2为其解的首项系数为1的整系数一元三次方程为________.
【解析】设x1,x2,x3是方程x3-x+3=0的根,则根据三次方程根与系数的关系,可得
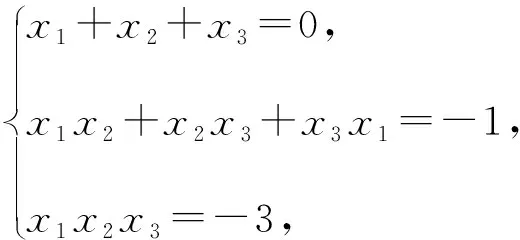
由此可知,所求的一元三次方程为x3-2x2+x-9=0.
【例4】(2023北京大学测试)方程组x+y+z=4,x2+y2+z2=6,x3+y3+z3=10的解的个数为( )
A.0 B.3
C.6 D.其他三个选项均不对
【解析】因为(x+y+z)2=x2+y2+z2+2xy+2yz+2zx,所以结合已知得xy+yz+zx=5.
又因为x3+y3+z3-3xyz=(x+y+z)(x2+y2+z2-xy-yz-zx),所以结合已知得xyz=2,

又t3-4t2+5t-2=t3-1-4t2+4t+t-1=(t-1)(t2+t+1)-4t(t-1)+t-1=(t-1)(t2-3t+2)=(t-1)2(t-2),
所以x,y,z是1,1,2的一个排列,即原方程组的解有3组,故选B.
应用3.求方程根(函数零点)的范围
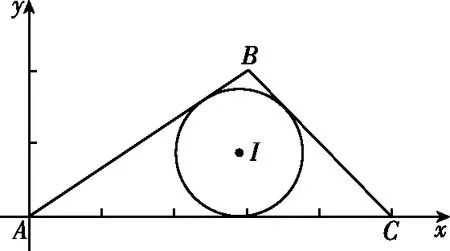
【例5】(2020山东莱芜一中月考)已知函数f(x)=x3+2的图象与函数g(x)=kx的图象有三个不同的交点(x1,y1),(x2,y2),(x3,y3),其中x1 A.k>3 B.x1<-2 C.x2+x3>2 D.x2x3>1 由f(x)=g(x),得x3-kx+2=0. 根据三次方程根与系数的关系,可得 因为x1<0 解得x1<-2,B正确; x2+x3=-x1>2,C正确; 【解析】三次函数f(x)=x3+ax2+bx+c有三个零点x1,x2,x3,即一元三次方程x3+ax2+bx+c=0有三个根x1,x2,x3, 由三次方程根与系数的关系,得 因为f(-1)=f(1), 所以-1+a-b+c=1+a+b+c, 解得b=-1; 因为f(0)=f(2),所以c=8+4a+2b+c, 应用4.求系数的范围 【例7】(浙江卷)已知函数f(x)=x3+ax2+bx+c,且0 A.(-∞,3] B.(3,6] C.(6,9] D.(9,+∞] 【解析】令f(-1)=f(-2)=f(-3)=t, 则0 即方程x3+ax2+bx+c-t=0的三个根. 根据三次方程根与系数间关系得 c-t=-(-1)·(-2)·(-3)=6, 所以c=t+6. 由0 所以c的取值范围是(6,9], 故选C. 【例8】(2023广东深圳一调)已知函数f(x)=x(x-3)2,若f(a)=f(b)=f(c),其中a A.1 C.a+b>2 D.abc的取值范围是(0,4) 【解析】因为f(x)=x(x-3)2=x3-6x2+9x, 所以f′(x)=3x2-12x+9=3(x-3)(x-1). 令f′(x)=0,即3(x-3)(x-1)=0, 解得x=1或x=3. 当f′(x)>0时,有x<1或x>3, 所以f(x)的单调递增区间为(-∞,1)和(3,+∞); 当f′(x)<0时,有1 所以f(x)的单调递减区间为(1,3). 又因为f(3)=0,f(1)=f(4)=4, 所以函数大致图象如图所示, 令f(a)=f(b)=f(c)=t, 因此0 又a,b,c是方程f(x)-t=0的三个根, 即x3-6x2+9x-t=0的三个根, 因为3 解得2 故选BCD. 应用5.求解最值问题 【例9】(2019北大综合营试题)实数x,y,z满足x+y+z=x2+y2+z2=2,求xyz的最大值和最小值. 得m′=3t2-4t+1=(3t-1)(t-1). 当t=0或t=1时,m=xyz取得最小值为0, 此时x=y=1,z=0, 无独有偶,2016年清华大学自主招生暨领军计划第13题:已知实数x,y,z∈R,x+y+z=1,x2+y2+z2=1,则下列结论正确的有( ) A.xyz的最大值为0 【答案】ABD.该题与例9如出一辙,请读者自行完成该题的解答. 应用6.求解综合问题 【例10】(2023南京、盐城一模)已知f(θ)=cos4θ+cos3θ,且θ1,θ2,θ3是f(θ)在(0,π)内的三个不同零点,则( ) B.θ1+θ2+θ3=π 【解析】由cos4θ+cos3θ=0,得cos4θ=-cos3θ, 所以在(0,π)内4θ+3θ=π或3π或5π, 因为cos4θ+cos3θ=2cos22θ-1+4cos3θ-3cosθ=2(2cos2θ-1)2-1+4cos3θ-3cosθ=8cos4θ+4cos3θ-8cos2θ-3cosθ+1=(cosθ+1)·(8cos3θ-4cos2θ-4cosθ+1), 故选ACD. 【例11】(2023北京大学测试)设三角形ABC的三个顶点为复平面上的三点z1,z2,z3,满足z1z2z3=0,z1+z2+z3=8+2i,z1z2+z2z3+z3z1=15+10i,则三角形ABC内心的复数坐标z的虚部所在区间为( ) A.(0.5,1) B.其他三个答案都不对 C.(1,2) D.(0,0.5) 【解析】根据三次方程根与系数的关系可知,z1,z2,z3为x3-(8+2i)x2+(15+10i)x=0的三个根,首先必定有一个为0,不妨设z1=0,则z2,z3为x2-(8+2i)x+15+10i=0的两个根,分解因式得(x-5)(x-3-2i)=0,所以z2=5,z3=3+2i,所以三角形ABC的三个顶点为A(0,0),B(3,2),C(5,0). 由于r就是I点纵坐标,也就是z的虚部,故选A. 【例12】(2013全国高中数学联赛四川预赛)若实数x0满足f(x0)=x0,则称x=x0为f(x)的不动点. 已知函数f(x)=x3+ax2+bx+3,其中a,b为常数. (Ⅰ)若a=0,求函数f(x)的单调递增区间; (Ⅱ)若a=0时,存在一个实数x=x0,使得x=x0既是f(x)的不动点,又是f(x)的极值点,求实数b的值; (Ⅲ)求证:不存在实数组(a,b),使得f(x)对互异的两个极值点皆为不动点. 【解析】(Ⅰ)若a=0,则f(x)=x3+bx+3, 所以f′(x)=3x2+b. 当b≥0时,显然f(x)在R上单调递增; 故当b≥0时,f(x)的单调递增区间为(-∞,+∞); (Ⅲ)证明:假设存在一组实数(a,b)满足条件,由条件知f′(x)=3x2+2ax+b. 因为f(x)有两个不同极值点,则Δ=4a2-12b>0,即a2>3b.① 令g(x)=2x3+9x-162, 则g′(x)=6x2+9>0, 所以g(x)在R上单调递增,从而g(x)=0至多有一个实根. 又因为g(0)=-162<0,g(4)=2>0,从而g(x)=0至少有一个实根. 所以g(x)=0恰有一个实根x=a∈(0,4). 故不存在实数组(a,b),使得f(x)对互异的两个极值点皆为不动点. 随着高考命题改革的不断深化,教材已成为高考数学命题一个重要的生长点.因此,在一轮复习教学中,要摒弃将教材“束之高阁”的舍本逐末、本末倒置的做法,引导学生重视对教材内容、题目乃至“阅读与思考”等方面的复习和挖掘,使得“回归教材”成为复习备考的一种常态.在数学一轮复习备考中,注重回归教材的教学是至关重要的,回归教材、细品教材,更能让学生体会到“书中自有黄金屋”的妙处.高考命题离不开教材,教材是高考命题的依托.教材决定了试题的稳定,也决定了试题的创新.“从教材中寻求支撑”成为高考数学命题的“潜规则”.要多回到教材,对教材内容、典型例、习题多做挖掘的工作.回归教材,不仅是备考者应对命题者的策略,也是备考者提升应考能力水平的手段. 1.数学高考,首先需要的是阅读能力,要能读懂问题的背景、读出隐含在文字表述中的信息等,都需要阅读能力.而阅读能力只有通过阅读来培养,其中教材是培养阅读能力的基本素材,我们不能想象,一个没有教材阅读经历的人,能够读懂考卷中的崭新材料. 2.每次专题训练,不少学生的失分是由于概念混淆、定义不清造成的,回归教材吃透其中的概念、定义、公式、例题,并将相关知识点进行横向、纵向比较、归纳,就不会出现冤枉失分.也就是说,回归教材实际上落实基础,尽力为自己揽分,减少无谓的失分. 3.回归教材,让学生自主梳理知识,可以使学生的知识结构网络化、系统化,这样做到具体题目时,会有一种“一览众山小”的感觉,不至于“一叶障目,不见泰山”,缩手缩脚,打不开思路. 4.解决数学问题,常用到一些“小结论”.除课本命名的性质、定理或公式外,这些“二级结论”散见于教材的例、习题或“阅读与思考”栏目中.通过回归教材,熟悉和掌握这些“二级结论”,对于解答选择、填空题可以节省时间,增加准确性.在处理解答题时,它也是探寻解题思路、进行合理推理的依据. 5.许多基本的解题思想、方法就存在课本结论、公式的推导过程中,通过回归教材,能让学生更深刻地理解、掌握和灵活运用. 6.规范作答,是重要的高考增分点.哪些定理不能直接套用、哪些过程不能省略、哪些表述不能随意、哪些符号不能承认,这些都只能依据教材,需要靠教材做示范. 7.回归教材,可以帮助学生查缺补漏.通过回归教材,弥补没有掌握好的概念、知识和方法技巧. 通过回归教材,可以消除学生在复习备考的过程中由于自信心程度不够而造成的空洞感、恐惧感或浮躁情绪.应在系统的高度重新审视教材,站在数学整体的高度与教材对话,让不同领域的知识交汇. 课题A—179《新教材改革下数学应用题的教学研究》的成果材料.


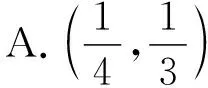

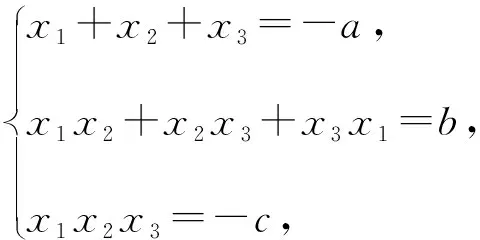
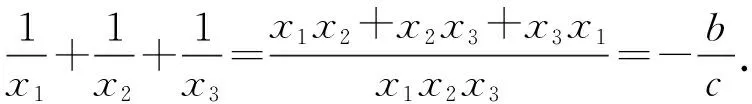








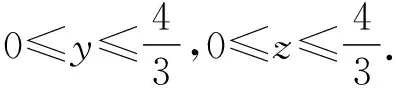

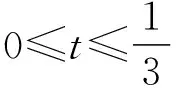
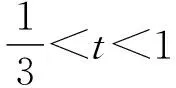
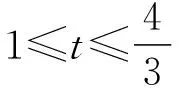

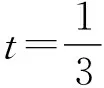













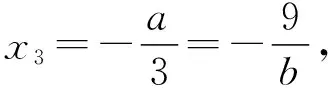
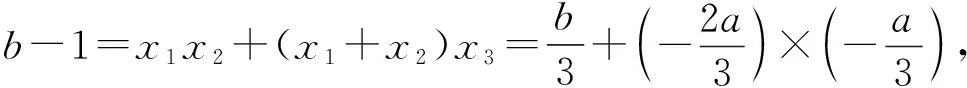
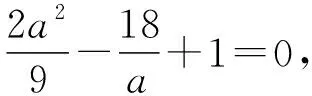
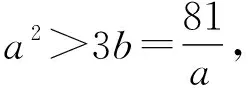
三、教学启示

