探究初中数学解题教学中逆向思维的应用

黎春

【摘要】使用逆向思维的核心是深入探究与积极思考问题，并建立与正向思维完全相反的思维方式.逆向思维运用在初中数学解题过程中，可以有效地打破常规的思维方式，创造出不一样的问题解决方式.初中学生运用逆向思维不仅可以快速解决问题，还能提高学生的创造能力，深化创新意识.本文重点分析逆向思维在初中数学解题教学中的作用，并针对逆向思维的有效应用提出具体的策略，供广大数学教师借鉴，并尝试应用到课堂教学中.

【关键词】逆向思维；初中数学；解题教学

在初中数学教学中，教师要对课程的内容进行精炼，增强“逆向思维”的应用，这样可以帮助学生更好地解决数学问题，并加深对数学问题的认识，从而增强学生的数学思维能力，促使学生能够从全方位角度解题，提高学生的解题能力和效率.

1 逆向思维在初中数学解题教学中的作用

1.1 可增进数学解题思维的全面延展

在初中数学课中，教学内容以解法为主，许多数学题采用传统的解题方式，不仅效率低下，且易错概率增大，而逆向思维则可以轻易地达到目的，其中最具代表性的就是逆向运算.初中数学教科书中大部分公式、运算规则等都是正向思维，在学习时容易产生固定的思维方式，以致在解决某些数学问题时，出现模式化的解答，从而极大地制约了学生思考能力的发展，限制学生思维多元化发展.所以，在解题时，应着重于让同学们用逆向思维法解答所遇到的问题，既能加深学生的思考深度，又能加强对数学知识的理解，为以后学习高难度的数学知识打下坚实的基础.

1.2 可增进学生对数学概念的深刻认知

数学概念的讲解与运用是初中数学课堂教学的重要内容之一，特别是运算法则和概念的剖析，正向思维会让数学问题变得更抽象.因此，首先要利用逆向思维来讲解，让学生对概念和公式有更深刻的理解.

1.3 增进双向思维的全面化培养

由于学生在学习数学时一直使用正向思维，导致许多学生在求解问题时产生了较强的思维惯性，不仅解题方式死板，解题效率也低.逆向思维的应用，可以有效调整解题方案，帮助学生更好地解决数学问题，同时还能使学生深入地研究数学问题.

2 初中数学解题教学中应用逆向思维的策略

2.1 逆向判断数学理论定理

逆向判断数学理论定理是初中数学中最常见，也是学生最容易接触到的基础的数学反推思维模式.由于数学的本质是一种抽象的概念，许多的数学问题都不能用直观的方式来说明，因此，发展逆向思维可以帮助同学们更好地解决问题.同学们能从逆向的观点来了解公式，并且可以避开那些难以应用的困难.打破传统的思考方式，转变学习方式，提高学生的创造性思考水平.

例如 初中数学人教版七年级下册第五章“相交线与平行线”章节教学中，本章节的教学重点是相交线、平行线及其判定、平行线的性质和平移等.其中的难点是区分判定定理与性质定理.在教学过程中，首先要对平行线性质和判定定理进行理解和分析，掌握其中所表达的含义.对于平行线的性质常规思路：已知两条线平行得知两个夹角的关系.简单地说就是由线定角的方式判定平行线.比如：如图1，下列条件：（1）∠1=∠3；（2）∠2=∠4；（3）∠6=∠8；（4）其中能判定a平行于b的有幾个？

本题主要考查学生对平行线判定方法的掌握，同时也是锻炼学生的逆向思维，与平行线性质完全相反.在本道题目讲解中，应用逆向思维讲解平行线的性质和判定差异后，学生就能完全掌握平行线的性质和判定.

2.2 逆向求解数学错题难题

如果正向思维解题过于繁琐，可以用逆向方法来解.逆向思维就是用一个未知数去解一个已知数，确认未知数与已知数是否一致，等问题被解决了，再把逆向思维变成正向思维求解.

例如 在初中数学人教版七年级下册第三章“一元一次方程”教学中，为学生出一道题目；小明今年8岁，祖父今年62岁，年后，祖父的年龄是小明年龄的4倍.本题主要考查学生对一元一次方程知识的掌握，解题的关键是对题目的理解，常规解题思路是设x年后，祖父的年龄是小明年龄的4倍，所以小明的年龄为8+x，祖父的年龄是62+x，然后针对这两个等式进行求解，最后得出10年后，祖父的年龄是小明年龄的4倍.本题的求解容易出错，在这种情况下，教师可以引导学生将最后的答案带入题目中，确认10+8=18，62+10=72，再确认72÷18是否等于4？这种逆向思维应用能够在一定程度上避免学生计算出错，还能帮助学生创新解题方法.

逆向思维可以使学生在最后的解题答案中判定解题是否正确，帮助学生及时发现问题.学生们都有从因到果的角度来解决问题，如果错误，那么本道题解题错误，所以果是否正确，需要学生在解题过程中谨慎求解.所以在初中数学教学中，要让学生学会从果到因去验证解题是否正确.通过这种方法，可以极大地减少学生的错题率，并提高学生的逆向思维能力.通过反向思考，可以把注意力从解决问题的角度转移到对数学思维训练上，从而激发出对数学问题的好奇心和探索心，提高学生对数学的学习兴趣.

2.3 逆向解决数学证明误区

在解决证明问题时，有些学生会使用数学公式，以为自己的论证是对的，实际上证明过程中有许多错误.因此，教师可以让学生在做证明题时充分发挥逆向思维的作用，采用“反证法”.

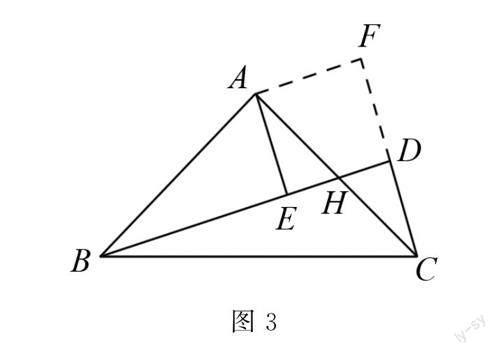
例如 如图2，点D在△ABC外，∠BAC=90°，AB=AC，射线BD与△ABC的边AC交于点H，AE⊥BD，垂足为E，∠ABD=∠ACD，

（1）若∠ABD=30°，CH=4，求DH的长；

（2）求证：BE=DC+DE.

在本题解答过程中，一定要找到可证明的点，不然则会出现意念证明，所谓的意念证明，就是默认为某个条件是正确的.因此，在对学生训练过程中，必须要注重在证明过程中每个条件都是有理有据，有因有果.

解 （1）因为∠ABD=∠ACD=30°，∠AHB=∠DHC，

所以∠BAH=∠D，∠BAH=90°，∠D=90°，

所以△CDH是直角三角形，

因为∠ACD=30°，所以DH=12CH=12×4=2；

从已知条件证明出△CDH是直角三角形.

在整个证明过程中，虽然过程比较简单，但是简单并不能代表可以省略，特别是某个条件的省略.对于初中学生而言，证明题是一种思维上的挑战，在证明过程中，必须要做到思维上缜密，不可忽略任何一个已知条件，同时还要积极挖掘出题目所提供的已知条件.即使再简单的证明题，题目中所出现的条件，都会在接下来的证明过程中使用到，没有一句话是形同虚设的，都有设题者的意图.

在（2）的证明中，需要作辅助线，如图3，作AF⊥CD，证明△ABE≌△ACF，再证明四边形AEDF是正方形，因为DE=DF，所以BE=CF=DC+DF=DC+DE.

从上述实例可以看出，反证法是一种特殊的运算方法，它可以帮助同学们通过逆向思维来求解问题，使学生更好地填补他们的分析上的缺陷，增强学生思路的清晰性和思维的严谨性.

2.4 逆向运用数学公式和运算法则

初中数学中的许多公式和计算规则是可以双向的，也就是可以逆转的.所以在教学中，教师不但要教授他们如何使用这些公式和计算规则，还要让他们记住这些公式和计算规则.在遇到问题时，可以用正反两种方法来求解.教师要擅长在数学应用中发现一些有代表性的实例，使他们能够应用逆向思维思考.

2.5 逆向运用数学公式和运算法则

在解决问题时，要积极思考，通过逆向思维来调整问题的位置，使学生更好地对知识进行二次学习和记忆.

例如 在初中数学八年级下册第十八章“平行四边形”教学中，首先要了解和掌握平行四边形性质及判定方法，平行四边形分为一般和特殊两种，比如正方形是一种特殊的平行四边形，正方形不仅是四条边相等且平行，还具有矩形和菱形的全部特征.无论是在日常测验中，还是在中考中，都少不了考查学生对正方形性质的了解.对于正方形知识点中存在的错误，要学会分门别类，不能一概而论.“正方形”这一小节知识点有很多，比如对正方形性质的理解，根据正方形性质求角度、线段长、求面积以及根据正方形性质与判定求角度、线段长、求面积等等.学生可以根据题意按照不同的知识点进行划分，然后按照对应的知识点进行对比分析，从而总结出符合自己的解题技巧.

3 结语

总之，逆向思维是一种很好的学习数学的思维方法.数学的问题看似变化多端，其实都是一样的，都可以追溯到教科书上的知识.在解决问题的过程中，概念可以帮助学生更好地了解和掌握知识.因此，在复习的时候，可以通过复习课本的内容来巩固自己的知识，从而增强自己的记忆力.

逆向思维是新课标教学思想的一种有效的教学实践，它在教学过程中的作用体现在现代教学效果的反馈上，因此，在教学方式和过程上，要进行持续的革新.针对学生反馈和课堂教学后的表现，适时作出相应的改变.把逆向思维这个概念融入到教师的课堂里，让学生慢慢地学会用逆向思维来解决问题，提升学生的逻辑性和创造力，从而使其数学知识更上一层楼.

参考文献：

［1］谢欣宇.探讨初中数学解题中逆向思维的应用［J］.理科考试研究（初中版），2022，29（6）：11-13.

［2］毛肇荣.浅谈初中数学教学中学生逆向思维能力的培养［J］.考试周刊，2022（8）：95-98.

［3］王方科.浅析初中数学教学中学生逆向思维能力的培养策略［J］.考试周刊，2022（31）：84-87.

［4］马子健.逆向思维在初中数学解题教学中的应用探究［J］.科学咨询，2022（20）：210-212.

［5］张翔.巧借逆向思维高效解答初中数学试题［J］.数理天地（初中版），2022（8）：16-17.

［6］梁磊.初中数学教学中学生逆向思维能力的培养分析［J］.读与写，2022（6）：59-61.

［7］項赟蒋.逆向思维在初中数学解题教学中的应用分析［J］.数理化解题研究，2021（14）：4-5.

［8］刘振芬.初中数学教学中学生逆向思维能力培养探讨［J］.新课程，2021（25）：99.

［9］许文倩.初中学生数学逆向思维培养的几点思考［J］.课堂内外（初中教研），2021（9）：56-57.