毒素环境下水生生物持续生存的状态反馈脉冲控制分析
张 蒙,洪久胜,李泽妤
(1. 北京建筑大学 理学院, 北京 100044; 2. 北京工商大学 嘉华学院, 北京 101118)
0 引言
自20世纪中叶以来, 全球有近一半的淡水资源受到了工业和生活污水的污染, 水体中的毒素引起的生物多样性丧失、水质退化等生态问题已成为亟待解决的问题[1]。 水体中含有大量的毒素和污染物, 会直接或间接造成水中的动植物窒息死亡, 同时水体的富营养化会加速细菌和病毒的繁殖, 影响动植物的生长和发育, 破坏水生生物的良好生长环境,甚至会造成物种的灭绝[2]。 因此保护水体环境和维持水生生物多样性是当今科学研究的热点问题[3]。
已有很多数学模型来描述淡水生态系统中的水生生物之间的相互作用关系,但利用状态反馈脉冲微分方程描述人类的调控措施对毒素环境下水生生物种群影响的文献并不多。近些年,许多学者将状态反馈脉冲微分方程广泛应用到生产和生活中。 例如,陈兰荪等[4]构建了害虫脉冲治理模型,得出阶1周期解存在性。郭红建等[5]建立了具有物质循环的状态反馈脉冲模型,并证明了模型具有唯一的轨道渐近稳定周期解。 JIANG等[6-7]对一类具有状态反馈脉冲动力系统的动力学性质研究, 丰富了脉冲动力系统的分岔理论。 WEI等[8-9]证明了状态反馈脉冲模型异宿环的存在性。 这些研究逐步完善了状态反馈脉冲系统的理论框架,并初步形成了半连续动力系统的理论体系[10-14]。
本文将建立一类毒素环境下水生生物的捕食者-食饵状态反馈脉冲模型, 研究其动力学性质,以讨论人为调控(投放及捕获)策略对物种持续生存的影响, 最后用数值模拟对所得结论加以验证。
1 无控制模型的建立与分析
1.1 无控制模型的建立
基于文献[8],建立毒素环境下具有Allee效应的捕食者-食饵模型如下:
(1)
式中:x=x(t)和y=y(t)分别表示t时刻食饵和捕食者的种群密度,L表示食饵种群的Allee效应系数,K表示食饵种群环境容纳量,bxy/(1+wx)表示Holling-Ⅱ型功能性反应函数,d表示捕食转化率,α和β分别是毒素对食饵和捕食者的影响系数,e表示捕食者的自然死亡率, 且捕食者种群无法离开食饵种群而存在。所有参数均为正。
1.2 无控制模型分析
根据模型(1)的第一个方程可以得到两条垂直等倾线x=0和
同理可得两条水平等倾线y=0和
式中:d>(β+e)w。
显然,模型(1)存在一个边界平衡点E0(0,0),下面讨论其他边界平衡点和正平衡点存在性。当y=0时,由
可以得到
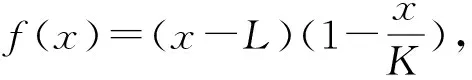
于是可以得到:(1)当fmax>α/a时,模型(1)有两个边界平衡点;(2)当fmax=α/a,模型(1)有一个边界平衡点; (3)当fmax<α/a时,模型(1)没有边界平衡点。
下面只考虑fmax>α/a的情况,记两个边界平衡点分别E1(x1,0) 和E2(x2,0), 其中x1和x2为方程
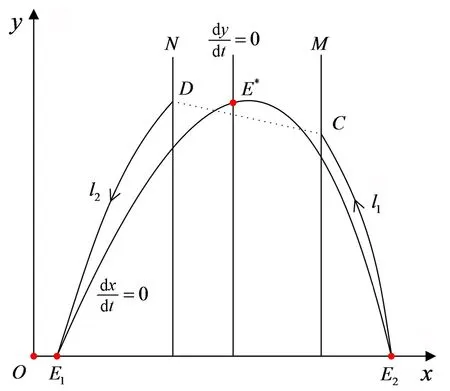
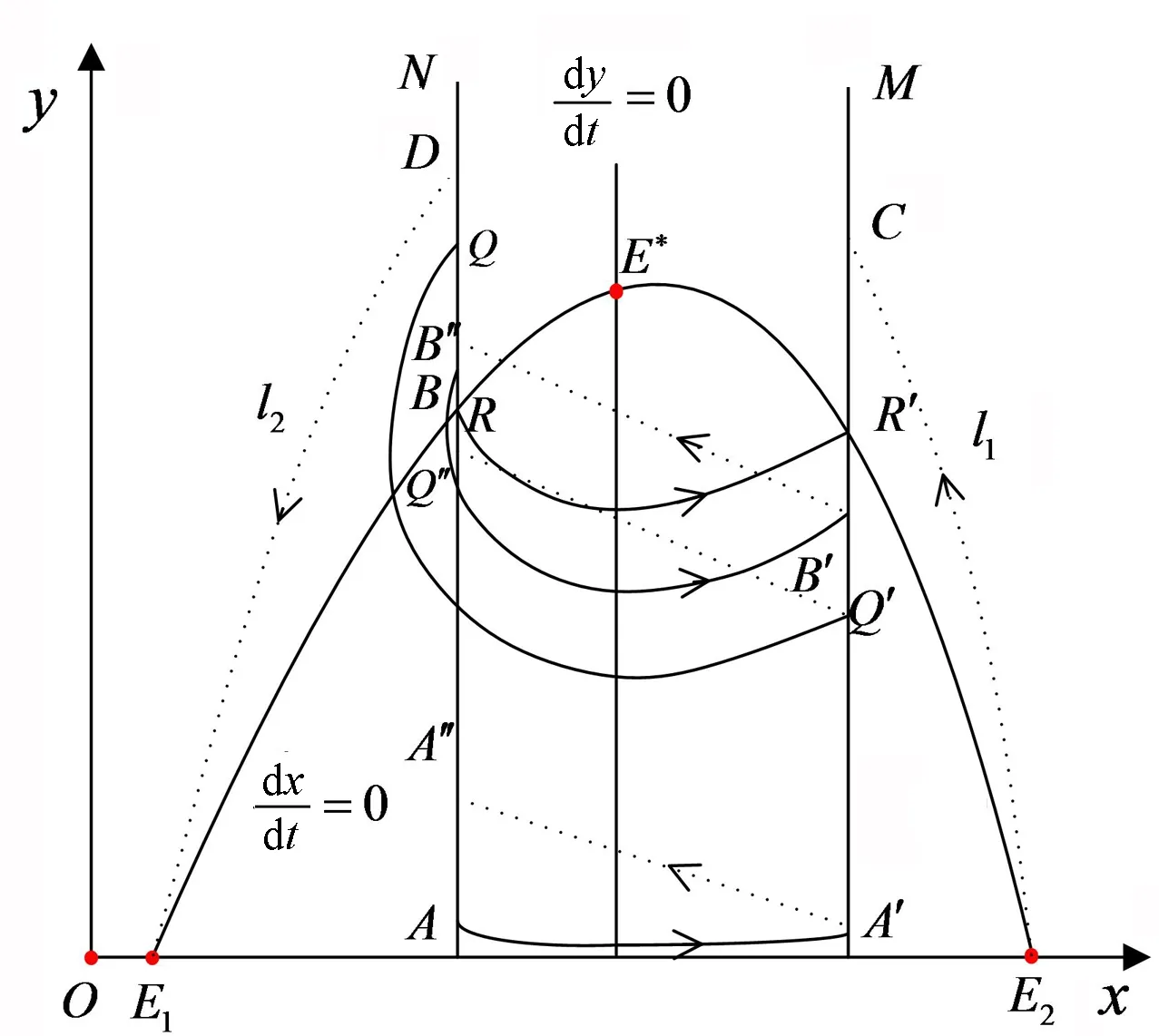
的两个根。由韦达定理可知两根均为正,不妨设x1 定理1模型(1)总存在一个边界平衡点E0(0,0); 当d>(β+e)w,fmax>α/a时存在两个边界平衡点E1(x1,0)和E2(x2,0),且若满足x1 定理2如果d>(β+e)w,fmax>α/a,x1 证明记 可得到Jacobian矩阵为 式中: 易得,E0(0,0)是稳定的结点。模型(1)在E1的Jacobian矩阵为 由x1 即det(J(E1))<0,则E1为鞍点。同理可以得到E2也为鞍点。 模型(1)在E*的Jacobian矩阵为 式中: 通过计算得到det(J(E*))>0, 若模型(1)满足A<0且A2(1+ωx*)3-bdx*y*<0,则E*是一个稳定的焦点。证毕。 注1下面的讨论均在满足定理1和定理2的条件下进行。 为使食饵和捕食者可以持续性生存, 人们在一些情况下需要对其进行管理,管理措施有多种,这里仅考虑状态脉冲反馈控制措施。当x≠h时,食饵、捕食者种群的演化按照模型(1)进行;当x=h时,对食饵种群进行收获,收获比例为p,并对捕食者种群进行投放,投放量τ为常数,从而有如下具有状态反馈脉冲控制的模型: (2) 式中:△x=x+-x,△y=y+-y。考虑实际的生物意义,模型(2)的参数均为正值。 为了从理论上讨论异宿环的存在性,下面仅考虑脉冲集为M={x|x=h,x* 于是存在τ*=yD-yC,当τ=τ*使得点D恰好为点C的后继点,即轨线弧E2C、脉冲线段CD、轨线弧DE1、E1E2和平衡点E1、E2构成模型(2)的异宿环(如图1所示)。 当τ>τ*时,C会脉冲到D的上方, 而后在模型(2)的作用下,向(0,0)点靠近。从l1右边出发的解, 最终也会趋于(0,0),这表示投放量过大,捕食者和食饵食物均趋于灭绝。 图1 模型(2)异宿环的存在性Fig. 1 The existence of Heteroclinic orbit of system (2) 注2 当yD≤yC时, 理论上存在τ*=yD-yC,当τ=τ*时,使得模型(2)存在异宿环;当yD≤yC且τ>τ*时,模型的解趋于点(0,0),但此时的τ*<0,这与投放的实际意义不符。另外,这里假设初值(x0,y0)∈Ω1={x0|x0>h},只是为了从数学上说明模型异宿环的存在性。 注3 当yD>yC且τ<τ*时,模型(2)可存在阶1和阶2周期解,具体讨论参见2.2节。 下面只考虑yD>yC的情况,如图2所示,点R(xR,yR)为垂直等倾线与N的交点,点R在模型(2)的映射下与等倾线dx/dt=0交于点R′(xR′,yR′)。 当1-xR/x*≤p≤1-xR/xR′时, 脉冲集M介于x=x*和x=xR′之间。 不失一般性,令初值(x0,y0)∈Ω2={(x0,y0)|(1-p)h 图2 模型(2)阶1周期解的存在性示意图Fig. 2 The existence of order-1 periodic solution of system (2) 定理3当yD>yC,1-xR/x*≤p≤1-xR/xR′和τ<τ*时,模型(2)存在阶1和阶2周期解。 证明在N上选取一点A(xA,yA),满足0 由于正平衡点是焦点,根据轨线的性质,在N上选取一点B(xB,yB)充分接近R点,满足yB>yR,从B点出发的轨线在模型(2)的作用下与脉冲集交于B′(xB′,yB′),模型(2)的脉冲函数将B′映射到B″((1-p)xB′,yB′+τ)(如图2所示),后继函数存在两种情况,分别为F(B)≤0和F(B)>0。 (1)当F(B)≤0时,显然存在一点P使得F(P)=0, 即模型(2)存在阶1周期解。由于该阶1周期解关于x是单调的,容易证明其唯一性。 (2)当F(B)>0时,模型存在阶1周期解或者阶2周期解。 限于篇幅,这里略去证明过程,可参见文献[6-7]。证毕。 定理4设(x,y)=(ξ(t),η(t))是模型(2)的一个具有周期T的阶1周期解,(ξ(0),η(0))=(xp,yp),(ξ(T),η(T))=(xq,yq),若 则该阶1周期解是轨道渐近稳定的。 证明由(ξ(t),η(t))是模型(2)的一个阶1周期解, 可知 ξ(0)=(1-p)h=xp,η(0)=yp, ξ(T)=h=xq,η(T)=yq, ξ(T+)=(1-p)h,η(T+)=yq+τ。 由类Poincaré准则[5,7],可令 A(x,y)=-px,B(x,y)=τ,φ(x,y)=x-h, 进而可得 从而有 式中 从而得到 当定理条件满足时,由类Poincaré准则可知,模型(2)的阶1周期解是轨道渐近稳定的。证毕。 由定理3可知,模型(2)存在阶1和阶2周期解。选择a=4.00,K=4.00,L=0.40,w=0.07,b=3.60,e=2.60,d=3.22,α=0.01,β=2.60,p=3/7,使用Matlab进行数值模拟,其分支图和相图如图3所示。 图3 模型(2)的周期解及分支图Fig. 3 The periodic solutions and bifurcation of model (2) 将投放量τ作为分支参数,其分支图如图3(a)所示。由图3(a)可知,存在一个阈值τ0≈0.36,当τ<τ0时,模型(2)存在一个阶1周期解(如图3(b)所示,τ=0.3);当τ>τ0时,模型(2)存在一个阶2周期解(如图3(c)所示,τ=0.38)。 考虑环境中毒素的影响, 构建了一类具有毒素项的食饵-捕食者模型。在无控制模型(1)的定性分析和动力学分析的基础上,构建了状态反馈脉冲模型(2),并研究其相应的动力学性质。结果表明:在食饵数量达到一定阈值时,当投放捕食者τ<τ*时,食饵-捕食者模型在规定的范围内达到动态平衡, 可保护生物多样性及种群的动态平衡。但是投放捕食者τ>τ*时,会导致捕食者缺少食物而灭绝。 这说明在人工干预维持物种持续生存时,不同的控制强度会产生不同的控制效果,选择合适的控制手段十分必要。2 脉冲模型的建立与分析
2.1 异宿环的存在性
2.2 周期解的存在性和稳定性
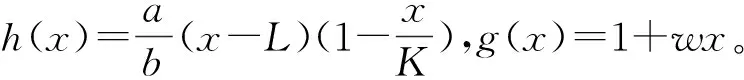
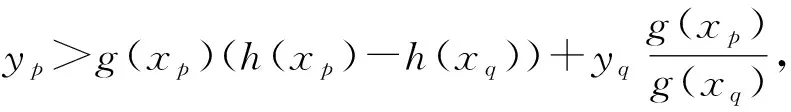
3 数值模拟

4 结束语

