均匀磁化磁介质麦氏关系的推演及其等磁场、等磁化热容量比较

赵世华,梁 平,彭鸿雁,李再金,王映品,蔡扬仪,陈韵琪

(海南师范大学 物理与电子工程学院, 海南 海口 571158)

0 引言

麦氏关系是将不易计算的或抽象的偏微分进行数学变换的一组方程式,变换之后的偏微分可用易测量或易计算的物理量表示,在内能、焓、自由能、吉布斯函数等特性函数的全微分表达和等压、等容热容量的差值研究问题中起到了重要作用[1-2],故麦氏关系在热力学统计物理中具有重要的研究意义[3]。目前热力学系统的主要研究对象依然是理想气体[4-5],故有关理想气体麦氏关系和其他热力学性质的研究已较为成熟[6-7]。然而,有关均匀磁化的磁介质麦氏关系研究却相对较少。谢名春教授[8-9]和路莹教授[10]分别从磁介质系统4个热力学函数的2种和4种不同定义方式出发,导出了形式上不完全相同的麦氏关系,其研究方法主要是通过共轭量代换和不同的内能定义来进行的,都没有从热力学函数本身的定义式中直接推演出麦氏关系,而且推导过程中并没有考虑体积是否变化。热容量是描述一个系统吸、放热本领的物理量,有关简单系统的热容量研究相对成熟[1],但是在磁介质中研究热容量,尤其是在磁场强度和磁化强度不变时的磁介质热容量研究却很少报道,这不利于磁介质系统相关热力学问题的解决,故有关均匀磁化磁介质系统的热容量研究是非常必要的[11]。

为此,本论文在推演均匀磁化磁介质系统的麦氏关系基础上,进一步讨论了磁介质在磁场强度H′(加撇以区别焓函数H)、磁化强度M分别不变时的等磁场热容CH′、等磁化热容CM的物理含义及其差值的计算。汪志诚[12]在讨论上述两热容量差值问题时使用了等效代换的方法,这样固然易于理解,但是很难从物理本质上去阐述清楚。雅可比行列式是一种进行偏导数变换运算的便捷工具,其定义和性质都易于理解,且在热力学中的应用已较为广泛[13-14]。故本论文还将采用雅可比行列式的数学方法进行等磁场热容量CH′与等磁化热容量CM的差值推演。

1 均匀磁化的磁介质麦氏关系

P、V、T、S、U、H、F、G分别表示研究系统的压强、体积、温度、熵、内能、焓、自由能和吉布斯函数,M、m、H′分别表示磁介质的总磁矩、单位体积的磁矩(磁化强度)和磁场强度,其中m=MV。

1.1 不考虑磁介质体积变化

1.1.1 内能U导出麦氏关系

简单系统的热力学基本微分方程为:

dU=TdS-PdV。

(1)

若忽略磁介质的体积变化,则均匀磁化磁介质的热力学基本方程为:

dU=TdS+μ0H′dm,

(2)

于是便可得到代换式(3):

(3)

由式(2)可得到式(4):

(4)

考虑到求二阶偏导的次序可以交换,所以易得式(5):

(5)

1.1.2 焓H导出麦氏关系

焓是物质系统的一个状态函数,用符号H表示。数值上等于系统的内能加上压强与体积的乘积,即

H=U+PV。

(6)

由式(1)和式(3)可得:

dH=TdS-μ0mdH′ 。

(7)

同理可得:

(8)

1.1.3 自由能F导出麦氏关系

自由能也称为亥姆霍兹函数,是描述物质系统状态的热力学函数之一,用F表示,数值上等于物质系统的内能减去它的绝对温度与熵的乘积,即

F=U-TS。

(9)

由式(1)和式(3)可得:

dF=-SdT+μ0H′dm。

(10)

同理可得:

(11)

1.1.4 吉布斯函数G导出麦氏关系

吉布斯函数也是描述物质系统状态的热力学函数之一,用G表示。吉布斯函数的定义式为

G=U-TS+PV。

(12)

由式(1)和式(3)可得:

dG=-SdT-μ0mdH′。

(13)

同理可得:

(14)

式(5)、(8)、(11)和(14)为磁介质的4种麦氏关系。

1.2 考虑磁介质体积变化

1.2.1 内能U导出麦氏关系

由热力学基本微分方程

dU=TdS-PdV+μ0H′dm,

(15)

可得:

(16)

(17)

1.2.2 焓H导出麦氏关系

由式(3)、(6)、(7)和(15)可得:

dH=TdS+VdP-μ0mdH′,

(18)

可得:

(19)

(20)

1.2.3 自由能F导出麦氏关系

由式(3)、(9)、(10)和(15)可得:

dF=-SdT-PdV+μ0H′dm,

(21)

可得:

(22)

(23)

1.2.4 吉布斯函数G导出麦氏关系

由式(3)、(12)、(13)和(15)可得:

dG=-SdT+VdP-μ0mdH′ ,

(24)

可得:

(25)

(26)

式(17)、(20)、(23)和(26)为磁介质的另外4种麦氏关系。

2 等磁场热容量CH′和等磁化热容量CM

根据简单系统中有关等压热容量CP、等容热容量CV的定义:

(27)

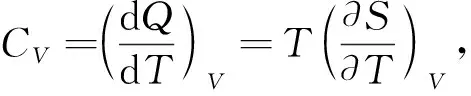
(28)

可写出等磁场热容量CH′和等磁化热容量CM的定义式:

(29)

(30)

由此可知:等磁场热容量CH′的物理含义是指在磁场强度H′不变时,磁介质系统每升高1 K的温度所吸收的热量,或在磁场强度H′不变时,磁介质系统熵对温度的偏导数再乘以系统温度;等磁化热容量CM的物理含义是指在磁化强度M不变时,磁介质系统每升高1 K的温度所吸收的热量,或在磁化强度M不变时,磁介质系统熵对温度的偏导数再乘以系统温度。由式(28)还知道:等磁场热容量CH′是系统温度T和磁场强度H′的函数,等磁化热容CM是系统温度T和磁化强度M的函数。热容是描述整个系统吸、放热本领的物理量,与系统物质的量的多少有关系,因此是广延量,于是有:

CH′=CH′(T,H′)=νCH′,mol(T,H′),

(31)

CM=CM(T,M)=νCM,mol(T,M) 。

(32)

3 有关CH′-CM的讨论

3.1 直接证明法

忽略磁介质的体积变化,且将熵S视为温度T和磁场强度H′的函数,将单位体积的磁矩M(磁化强度)视为温度T和磁场强度H′的函数,即有:

S=S(T,H′)=S[T,M(T,H′)]。

(33)

等式两边对温度T求导可得:

(34)

两边同乘以温度T:

于是可得到:

(35)

其中磁介质的总磁矩m和磁化强度M满足:

m=VM,

(36)

故有式(37)成立:

(37)

将式(11)代入式(37)可得:

(38)

根据隐函数中3个变量存在的偏导数学关系可知:

(39)

故式(35)可写成:

CH′-CM=-

(40)

根据式(33)可得:

CH′-CM=

(41)

3.2 雅可比行列式的定义

雅可比行列式在解决实际的热力学问题时是一种很有效的数学工具[9-11],其定义如下:设u,v是独立变量x,y的函数,即

u=u(x,y),v=v(x,y),

则有:

根据以上定义,可推演以下性质:

(42)

3.3 雅可比行列式求解

根据雅可比行列式的性质可得下列等式:

(43)

根据式(11),式(43)可变形为:

CH′=Cm-

(44)

又根据式(36)可得:

CH′-CM=

(45)

4 结论

推演的8种麦氏关系可应用于今后的磁介质领域研究中。在对无法直接实验测得的磁介质物理量进行偏导数运算的时候,通过麦氏关系将不可测量的偏微分转变为可知量的偏微分,这便是麦氏关系的精髓所在。在推演等磁场热容量和等磁化热容量的差值过程中,采用雅可比行列式能省去较多的具有物理涵义的步骤,可见雅可比行列式在偏微分计算领域的重要性。