高考类型剖析,线性回归应用

江苏省海门中学 李乃洋

线性回归模型及其应用是高考数学试卷中的一个重要考点.对于两个变量之间的线性回归模型与相关关系,全面把握相关概念,正确进行数据分析处理,准确确定线性回归方程,利用线性回归方程进行合理决策应用等,都是线性回归模型及其应用的重要组成部分.因此,应全面系统理解与掌握相关线性回归模型的概念,进一步加强数学应用意识,提升应用所学知识分析问题和解决问题的能力.

1 概念理解

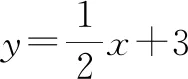
分析：根据题意,用解释变量对于预报变量变化的贡献率R2来表示拟合效果,通过概念的理解,以及R2的性质特征,R2越大表示模型的拟合效果越好,即可确定正确答案为C.

2 信息解读

例2(多选题)[2023届福建省莆田市涵江区锦江中学高三(上)第一次月考数学试卷]在“3·15”前,某市物价部门对本市5家商场的同一商品的销售情况进行调查,其对应的售价x元和销售量y件对应的数据如表1所示:

表1

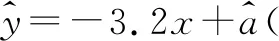
B.当x=1时,y的估计值为36.8

C.当售价为5元时,销售量一定是24件

D.样本中心点为(10,8)

分析：利用题目的数据,求出对应的均值与相关的参数,并确定对应的回归方程,再结合线性回归方程的性质,即可解读相关信息,给出判断.

答案:ABD.

3 关系判断

例3[2023届四川省眉山市仁寿县文宫中学高三(上)月考数学试卷(9月份)]某专营店统计了近五年来的创收利润yi(单位:万元)与时间ti(单位:年)的相关数据,如表2所示:

表2

依据表2中的数据,请计算相关系数rty,并结合计算结果说明能否用线性回归模型拟合y与t的关系?(结果精确到0.01,若|rty|>0.8,则表明可用线性回归模型拟合y与t的关系.)

例4(2023年高考数学全国乙卷理科·17)某厂为比较甲乙两种工艺对橡胶产品伸缩率的处理效应,进行10次配对试验,每次配对试验选用材质相同的两个橡胶产品,随机地选其中一个用甲工艺处理,另一个用乙工艺处理,测量处理后的橡胶产品的伸缩率,甲、乙两种工艺处理后的橡胶产品的伸缩率分别记为x1,y1(i=1,2,……,10),试验结果如表3:

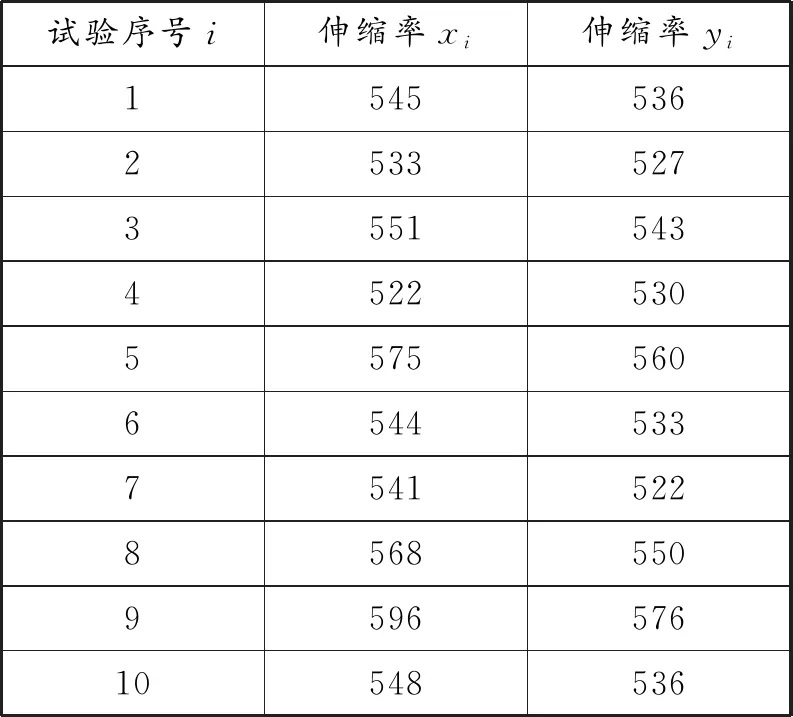
表3

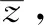
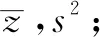
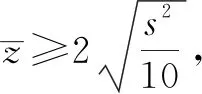
分析：例3和例4都是根据题意进行计算即可给出判断,过程略.

4 决策应用

例5[2022—2023学年陕西省榆林十中高二(上)第一次质检数学试卷]公交公司为增设一个公交起点站,研究某地车辆发车间隔时间x与乘客等候人数y之间的关系,得出以下表4中相应的数据:

表4

从中选取四组数据作线性回归分析,并用剩下的两组数据进行检验.

(1)试求剩下的两组数据不相邻的概率.

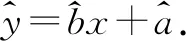
(3)创新定义“最佳回归方程”:借助线性回归方程预测的数据与实际数据相差不超过1人,则所求的的线性回归方程是“最佳回归方程”.试判断(2)中所求的是“最佳回归方程”吗?同时为了使等候的乘客不超过35人,则发车的间隔时间为18 min,是否合适?

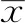
解析：(1)设这六组数据分别为1,2,3,4,5,6,那么剩下的两组的所有可能为(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6),共有15种.

其中“剩下的两组数据相邻”的有:(1,2),(2,3),(3,4),(4,5),(5,6),共5种.

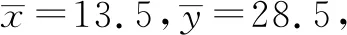
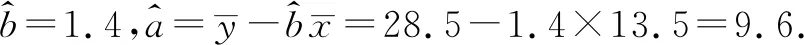
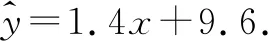
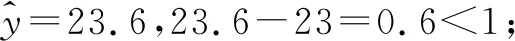
所以(2)中所求出的线性回归方程是“最佳回归方程”.

由1.4x+9.6≤35,解得x≤18.14.

故间隔时间设置为18 min比较合适.

点评：借助线性回归方程的求解,并利用条件中相关问题的设置(本题中为“最佳回归方程”),合理求解对应的数据并加以正确决策与判断.特别在对一些实际应用问题进行决策与判断时,要有数据依据与基础.

线性回归模型及其应用是根植于现实场景中,结合实际应用问题的创设,综合统计中的数据信息与数据分析,对线性回归的相关概念、数据处理、关系判断以及决策应用等巧妙设置问题,考查线性回归的相关知识、数学思想方法和数学能力等,实现创新应用.