基于CPFS的“等比数列求和公式”教学设计
云南师范大学数学学院 李东瑞 王天志
喻平教授于2003年提出数学学习心理CPFS结构理论,该理论主要研究学习者头脑中的数学知识网络,并引入概念域(concept field)、概念系(concept system)、命题域(proposition field)、命题系(proposition system)四个基本单元来刻画学习者的数学知识表征[1].CPFS结构理论从学生学习心理和数学命题自身特点出发,将学生学习数学命题的心理过程分为三个阶段:命题的获得、命题的证明、命题的应用[2].命题域是一组等价命题组成的体系,命题系是指在学习者头脑中贮存的一组命题,其中一个命题与其他某个或某些命题之间存在推出关系,这些命题之间就形成了一个关系网络.
学生学习新知时,依托于头脑中已存在的知识经验,将旧知作为桥梁,连接新知与旧知.若学生不具备完整的命题域和命题系,在解题过程中就难联结到其他与之相关的命题,从而知识断层,思维受限,面对变式题就会无从下手.所以在头脑中形成完备的CPFS结构体系,有助于数学知识的贮存和提取以及知识迁移,帮助理解数学知识,发展数学能力.
1 教学分析
1.1 教材及学情分析
本文以2019年《普通高中教科书·数学·必修二》(人教A版)第四章第三节“等比数列的前n项和公式”为例.该部分内容对数列知识起到总结凝练的作用,让学生的数学知识以及数学思维能力都可以进一步拓展[3].数列知识涉及很多数学符号语言,抽象程度较高,要求学生能够敏锐地观察和思考数组之间关系,以及具有较好的逻辑思维能力.通过对数列知识的学习,提高学生数学抽象、逻辑推理等核心素养[4].
学生学习该部分内容之前,已经掌握了等差等比数列等相关知识.学习等差数列前n项和时,采用倒序相加的方法求和,理解了公式中关键的四元素:Sn,a1,n,d.类比到等比数列求和,关键四元素:Sn,a1,n,q,但等比数列求和复杂程度相对高于等差数列求和,寻找合适的求和方法还是具有一定困难,需要引导学生从从关键的四元素入手,利用等比数列的性质特点,基于学生的“最近发展区”,让学生从具体实例的求和过渡到对抽象数学符号语言的理解.
1.2 教学目标
理解公式的形成过程,掌握公式推导过程中所运用到的思想方法;能够灵活运用等比数列求和公式解决问题.
1.3 教学重、难点
教学重点:掌握等比数列求和公式,能够利用等比数列求和公式解决实际问题.
教学难点:引导学生找到证明等比数列求和公式的方法.
2 教学过程
2.1 情境引入
问题1某种细菌20 min就通过分裂繁殖一代,那么一个这种细菌从第1次分裂开始,1天(24 h)之后产生的后代总数是多少?(如图1所示)
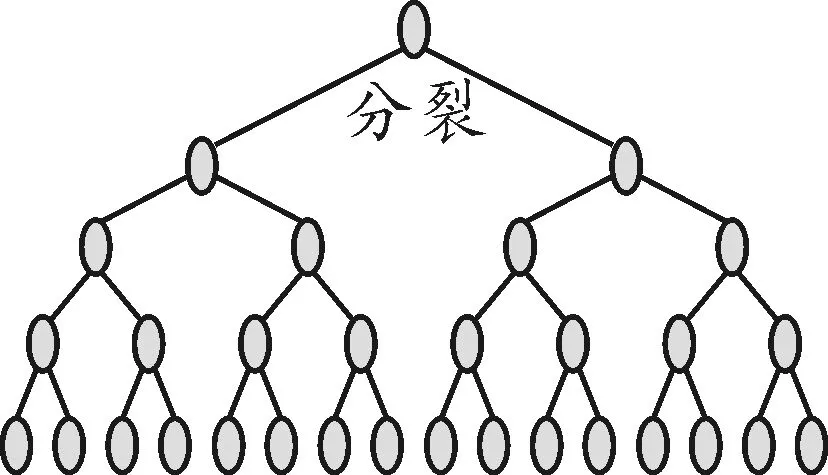
图1 细菌分裂
设计意图:创设细胞分裂的情境问题[5],让学生发现并思考项数较多的等比数列该如何简捷求和.
2.2 命题的获得
针对问题1,先让学生求出细菌分裂六次之后的细菌总数.学生小组合作讨论5分钟,然后请小组代表分享本组讨论结果.
小组1:在纸上列出了细菌每次分裂后产生的后代个数:2,4,8,16,32,64,其解决方法是将六个数依次加起来.
这种方法对于项数较少的数列求和可以采取,但面临下列问题3时便不知所措.
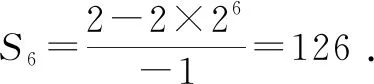
该小组一直围绕所求目标量S6进行转化,最终求解.
问题2回顾等差数列求和公式,思考等比数列求和公式的几个关键元素会是什么呢?
设计意图:从学生已有的知识经验出发,引导学生由等差数列求和公式当中关键的四元素,类比找到等比数列求和的关键四元素为Sn,a1,n,q.
问题3当细胞分裂n次后,第n次的通项公式是什么?并尝试求出Sn.
2.3 命题的证明
根据学生的作答情况,教师指出其中遗漏或考虑不完全的情况,在黑板上展示完整的证明过程.
证明1:由a2+a3+……+an=qa1+qa2+……+qan-1=q(a1+a2+……+an-1) ,得
Sn-a1=q(Sn-an).
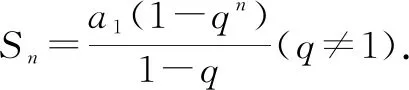
追问1:以上证明出来的公式能否适用于常数列求前n项和呢?常数列的前n项和如何求?
总结:得出等比数列前n项和公式为
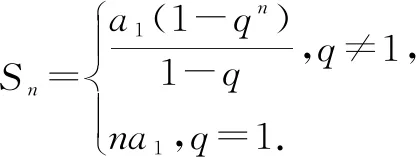
问题4请思考还有其他的证明方法吗?回顾等差数列求和时是如何变形的,其推导过程中本质是为了得到什么?
设计意图:引导学生回顾等差数列求和公式的推导过程,利用倒序相加法对两个等式进行处理,其本质就是利用合并同类项、消元的思想[6].
追问2:两个等式之间经过怎样的运算可以消元呢?如果将两个等式相减,那么另外一个等式该如何书写呢?
对于等式Sn=a1+a2+……+an-1+an,根据学生的反应情况,适当给出思考方向(思考相邻项的关系),抓住等比数列求和的四要素进行思考,得到第二个等式qSn=qa1+qa2+……+qan-1+qan=a2+a3+……+an+an+1,随即让同桌之间一起合作,尝试计算Sn-qSn.(注:以下证明前提为q≠1.)
针对学生出错的地方给予及时引导,五分钟后,教师带领学生一同在黑板上呈现证明过程.
证明2:设Sn=a1+a2+……+an-1+an,等式两边同时乘q,得qSn=a2+a3+…+an+an+1.
两式相减,得(1-q)Sn=a1-an+1=a1-a1qn.
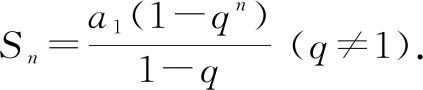
一个命题的证明都要以某些已经证明为真的命题为基础,证明过程中会与很多命题产生联系,运用多种方法证明一个命题,可以帮助完善学生的命题域和命题系.教师根据学生的接受情况,尽量给出多种等比数列求和公式的证明方法.以下将介绍另外五种证明方法.
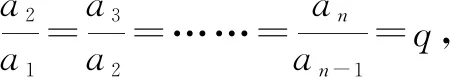
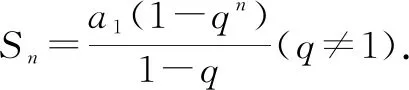
证明4:当q≠1时,由(1-q)(1+q+q2+……+qn-1)=1-qn,得
证明6:Sn=a1+a2+……+an=a1+q(a1+a2+……+an-1)=a1+qSn-1.
①
由Sn-Sn-1=an,可得
Sn-1=Sn-an=Sn-a1qn-1.
②
将②代入①,得Sn=a1+q(Sn-a1qn-1).
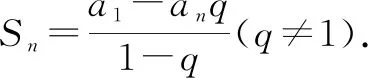
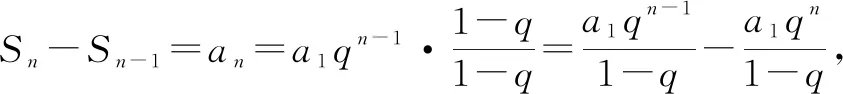
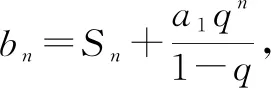
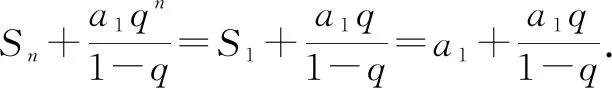
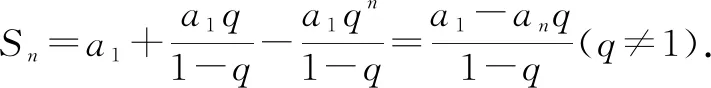
2.4 命题的应用
例1某人存入银行a元,存期为20年,年利率为r,那么按照复利,20年后他可以获得本金利息共多少?
设计意图:例1贴近现实生活,既可以巩固学生对新知的掌握,也能够让学生感受数学的应用价值,认识数学的科学价值[7].
例2已知数列{an}的首项a1=1,且满足an+1+an=3·2n.
(1)求证:{an-2n}是等比数列.
(2)求数列{an}的前n项和Sn.
教师适当给出思路引导:根据等比数列的性质,要证明数列{an-2n}是等比数列,可以转化为证明什么呢?观察数列{an}的前n项和Sn的形式,如何变形Sn可以简化计算呢?
设计意图:第(1)问证明{an-2n}为等比数列考查学生的数列构造能力和观察能力,其中涉及转化思想,帮助学生完善等比数列的命题域.
例3记Sn为等比数列{an}的前n项和.已知S2=2,S3=-6.
(1)求{an}的通项公式;
(2)求Sn,并判断Sn+1,Sn,Sn+2是否成等差数列.
2.5 课堂总结及作业布置
笔者通过提出如下问题,引导学生回顾本堂课所涉及的知识、思想方法:等比数列求和公式中的几个关键元素是什么?等比数列求和公式的证明过程中采用了哪些数学思想方法?错位相减法在应用的过程中需要注意哪几点?
最后给学生布置精练且有代表性的课堂作业,让学生加深对新知的理解,巩固学生对等比数列求和公式的命题域和命题系的认识.
3 结束语
本文中主要分为命题的获得、命题的证明、命题的应用三部分,在“等比数列求和公式”的教学设计过程中,更多篇幅放在公式的推导证明上.数学命题学习过程如图2所示.
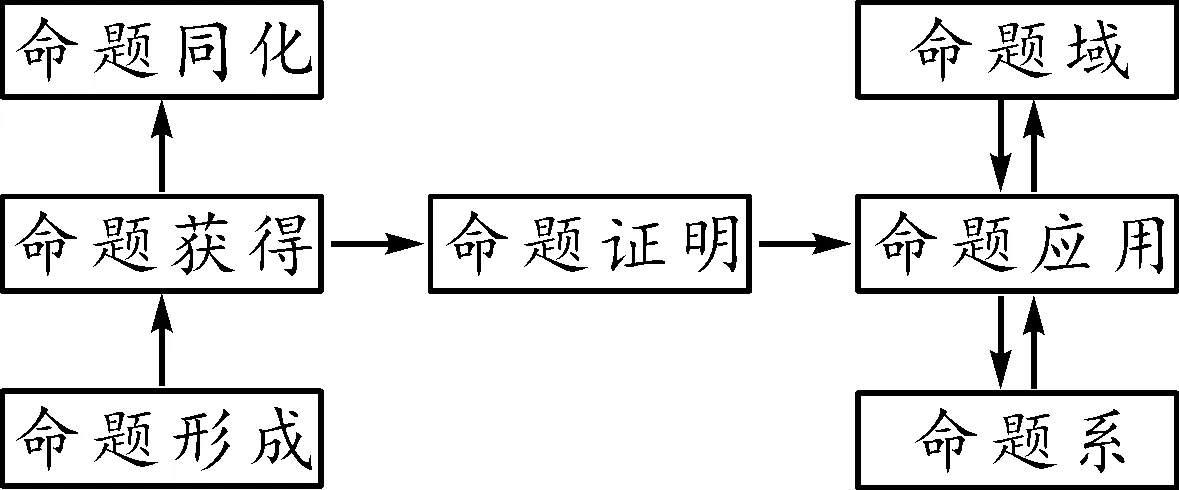
图2 数学命题学习过程
从数学学习的角度看,有的命题的证明价值高于它的发现价值.命题的证明过程是多个命题之间的联结,学生要以已经获得的若干命题为逻辑基础,同时将新命题纳入认知结构.遵循学生学习命题的心理特征.学生学习知识如同在头脑中构建一张知识网,知识网之间的知识节点都要环环相扣.教师在命题教学过程中,要关注学生的数学学习心理,让学生经历命题的形成过程,并对相应命题给出变式训练,加强学生的命题网络,让学生能够在不同情境中应用命题,帮助完善学生个体的命题域和命题系.

