借助数学阅读,培养关键能力
安徽省休宁中学 甘锦丹 张裕德
数学阅读理解能力是数学学习中一个非常重要而又极易被忽视的技能.在数学教学与数学学习过程中,数学阅读理解题到处都是,或借助数学语言给出,或通过图形信息展示,或结合问题情境创设,或利用创新定义构建等,巧妙将数学、生活生产中的新旧知识等加以联系,透过现象看问题本质,有效实现新信息从已知的基本知识、方法等方面进行合理的迁移,从而达到创新与应用的目的.这里,对学生数学阅读理解能力就有较高的要求,也是问题破解的关键一环.
1 阅读图表信息,强化数据分析
图表信息类阅读理解题多是通过图象、图形或表格等形式来合理创设,从中融入对应的数据信息以及一些相关的数学信息.借助考生的阅读理解能力以及数据的获取与处理能力等,很好地解决此类立意新颖、构思巧妙与解法灵活的图表信息问题.
例1[2023届四川省成都市高新区高三(上)第一次诊断数学试题](单选题)中国营养学会把走路称为“最简单、最优良的锻炼方式”,它不仅可以帮助减肥,还可以增强心肺功能、血管弹性、肌肉力量等,甲、乙两人利用手机记录了去年下半年每个月的走路里程(单位:km),现将两人的数据绘制成如图1所示的折线图,则下列结论中错误的是( ).
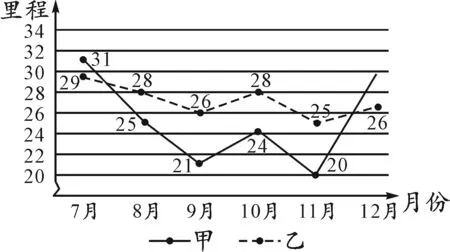
图1
A.甲走路里程的极差等于11
B.乙走路里程的中位数是27
C.甲下半年每月走路里程的平均数大于乙下半年每月走路里程的平均数
D.甲下半年每月走路里程的标准差大于乙下半年每月走路里程的标准差
分析:本题阅读的关键,一是单选题,二是选错误结论,三是能够从图表读出对应的数据.运用极差、中位数、平均数的概念及标准差的含义即可求解.
解析:由折线图,知7~12月甲走路的里程分别为31,25,21,24,20,30,乙走路的里程分别为29,28,26,28,25,26.
所以甲走路里程的极差为31-20=11,A正确;
D的正确性可以不经计算,而通过图的波动情况进行判断.由折线图得甲下半年走路里程的波动性大于乙下半年走路里程的波动性,故选项D正确.
2 阅读问题情境,关注自学能力
问题情境类阅读理解题多以现代科学技术、现实生活、学科间的交汇、社会热点等为背景创设,旨在突出新时代教育总方针——立德树人.此类阅读理解问题,关键就是认真阅读,从题意中获取信息,合理加工处理,重点关注考生的自学能力,从而实现数学思想、方法、能力的迁移运用.

(1)求比赛一共进行了四局并且甲班最终赢得比赛的概率;
(2)若规定每一局比赛中胜者得2分,负者得0分,记X为比赛结束时甲班的总得分,求随机变量X的分布列和数学期望.
分析:本题阅读理解的关键,一是决赛获胜的规则,二是比赛的规则.运用概率公式及随机变量等概念即可求解.第(1)问因为比赛一共进行了四局并且甲班最终赢得比赛,所以最后一局甲班获胜,在前三局中甲获胜两局;第(2)问X的所有可能取值有0,2,4,6,即比赛三局且甲三局全输,比赛四局且甲赢一局,比赛五局且甲赢二局,比赛五局且甲赢三局.
解析:(1)记Ai(i=1,2,3,4,5)表示“第i局甲获胜”.
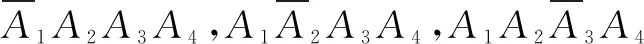
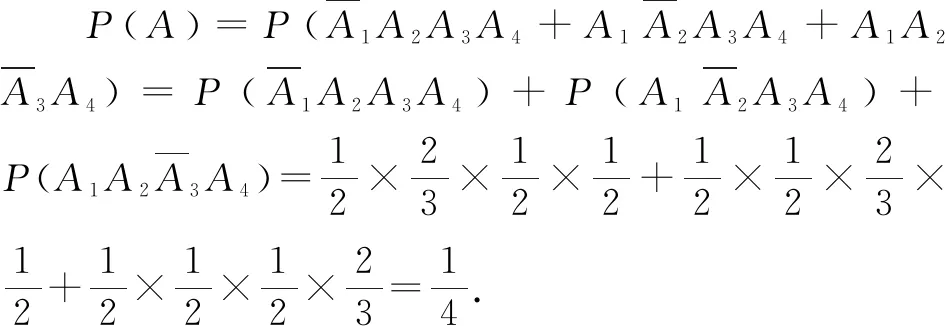
(2)由题意,X的所有可能取值有0,2,4,6,则
所以X的分布列为
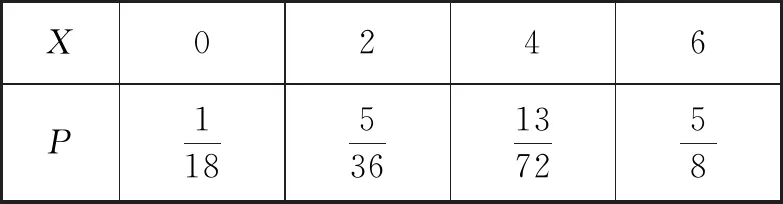
X0246P118536137258

3 阅读创新定义,实现知识迁移
创新定义类阅读理解题多是中学数学中还没有出现的新知识,借助现有数学知识基础新定义一种新的概念、运算、规则、性质或情境等,要求解题者通过合理的阅读、观察等,有效归纳与探索,实现知识与信息的迁移,对阅读理解能力、信息处理能力等都有很高的要求.
例3[2023届北京贸大附中高三(上)期末数学试题](多选题)定义一:关于一个函数f(x)(x∈D),若存在两条距离为d的直线y=kx+m1和y=kx+m2,使得在x∈D时,kx+m1≤f(x)≤kx+m2恒成立,则称函数f(x)在D内有一个宽度为d的通道.定义二:若一个函数f(x),关于任意给定的正数ε,都存在一个实数x0,使得函数f(x)在[x0,+∞)内有一个宽度为ε的通道,则称f(x)在正无穷处有永恒通道.下列函数中在正无穷处有永恒通道的函数为( ).
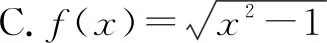
分析:本题阅读理解的关键是两个新定义的内涵.定义一的内涵是在函数定义域内函数图象都在两条平行线之间,如y=sinx在其定义域内有一个最小宽度为2的通道;定义二的内涵是在正无穷处有任意宽度的通道,即随着x的增大,函数值要么趋向于0,要么单调递增或单调递减,有渐近线.
解析:对于f(x)=lnx,单调递增,且无渐近线,故不存在一个实数x0,使得函数f(x)在[x0,+∞)内有一个宽度为ε的通道;
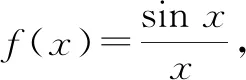

对于f(x)=e-x,随着x的增大,函数值趋向于0,故对于任意给定的正数ε,存在一个实数x0,使得函数f(x)在[x0,+∞)内有一个宽度为ε的通道.
综上分析,故选择答案:BCD.
新高考数学试卷中,经常通过巧妙创设应用问题,借助数学本质内涵、信息数据分析、学生自学能力以及数学知识迁移等方面来设置数学阅读理解问题,合理融入数学基本知识、思想方法和能力技能等,全面考查学生的关键能力,注重数学本质,发展数学能力,选拔优秀人才,落实数学核心素养的要求,全面合理推进中学数学教学改革与创新应用.

