“三新”背景夯基础,核心素养重创新*
——指向数学高阶思维的“概率”单元复习设计
江苏省灌南县惠泽高级中学 高 娇
在新教材(人民教育出版社2019年国家教材委员会专家委员会审核通过)、新课程(《普通高中数学课程标准(2017年版,2020年修订》)、新高考“三新”背景下,“概率”单元复习教学设计更加侧重于数学基础知识、基本技能、基本思想、基本活动经验“四基”层面,合理构建知识网络与体系,注意数学概念的基础性,凸显数学公式的应用性,展示数学思维的灵活性等,有效进行单元复习教学设计与安排.
1 构建知识网络,厘清单元系统
涉及“概率”单元知识模块,关键在于构建相应的知识网络,“串联”起各个知识点之间的联系,形成节点,全面厘清单元系统,为进一步理解与深化知识,以及综合应用等创设条件.
图1是“概率”单元的知识网络,从数学基础知识、基本技能、基本思想、基本活动经验这四个不同视角来展开,关注学生对“四基”的落实情况,以及发现问题、提出问题、分析问题和解决问题能力的培养与提升情况,重视数学核心素养的发展.
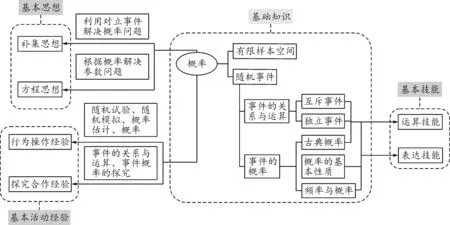
图1
2 重视概念学习,辨析理解差异
“概率”单元中涉及众多的概念,正确学习并理解对应的概念,以及不同概念之间的差异,为解决问题提供条件.如,随机事件、必然事件与不可能事件,频率与概率,互斥事件与对立事件,事件的关系(和事件与积事件)与运算,互斥与独立,等等,都需要我们正确理解相关概念,并加以合理联系与区别.
例1从一批产品中取出3件产品,设A={3件产品全不是次品},B={3件产品全是次品},C={3件产品不全是次品},则下列结论正确的有(填序号).①A与B互斥;②B与C互斥;③A与C互斥;④A与B对立;⑤B与C对立.
分析:正确理解并掌握互斥事件与对立事件的概念,辨析二者之间的关系与差异,并对复杂事件加以细化与展开,进而结合互斥事件与对立事件的概念来逐个分析与判断.
解析:事件A指的是3件产品全是正品,事件B是指3件产品全是次品,事件C包括1件次品2件正品、2件次品、1件正品3件全是正品这3个事件.
所以A与B是互斥事件,但不是对立事件;A与C是包含关系,既不是互斥事件,也不是对立事件;B与C既是互斥事件,也是对立事件,故结论正确的有:①②⑤.
3 强化概率公式,增强数学运算
“概率”单元中涉及众多的公式与性质,正确理解并掌握这些基本公式,为相应概率的求解与运算奠定基础.这里涉及的公式与性质主要有:古典概型的概率公式,概率的基本性质,互斥事件的概率公式,对立事件的概率公式,独立事件的概率公式,等等.
最主要的概率公式与求解就是古典概型的概率问题、相互独立事件的概率问题等,它们都是这个单元中比较基本的数学运算对象.
例2甲、乙两校共有6名数学教师报名参加“对口”支教活动,其中甲校的数学教师是2男1女,乙校的数学教师是1男2女.
(1)若从甲、乙两校中各任选1名,试求选出的2名教师性别相同的概率;
(2)若从甲、乙两校中任选2名,试求选出的2名教师来自同一学校的概率.
分析:根据题设,分别用不同的字母来表示甲、乙两校中的不同教师,第(1)(2)问都可以通过罗列法列举出不同的结果,再利用古典概型的概率公式加以分析与求解.
解析:设甲校两名男教师分别用a,b表示,女教师用c表示;乙校男教师用x表示,两名女教师分别用y,z表示.
(1)从甲、乙两校中各任选1名教师,样本空间为Ω={ax,ay,az,bx,by,bz,cx,cy,cz}.
其中,记A=“选出的2名教师性别相同”,于是A={ax,bx,cy,cz}.
(2)从甲、乙两校中任选2名教师,样本空间Ω={ab,ac,ax,ay,az,bc,bx,by,bz,cx,cy,cz,xy,xz,yz}.
其中,记B=“选出的2名教师来自同一学校”,于是B={ab,ac,bc,xy,xz,yz}.
4 拓展数学思维,关注补集思想
“概率”单元中涉及众多的数学思维,如补集思想、方程思想等,这些都是解决概率问题比较常用的数学思维.全面拓展并应用数学思维,可以使数学知识的学习更加牢固,数学问题的解决更加简捷.
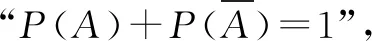
例3甲、乙两名射击运动员分别对同一目标射击1次,甲、乙射中的概率分别为0.8, 0.9,设事件A为“甲射中目标”,事件B为“乙射中目标”,事件A与B是相互独立的.求:
(1)两人都射中的概率;
(2)两人中恰有一人射中的概率;
(3)两人中至少有一人射中的概率.
分析:根据条件,设出对应事件,并确定两事件之间的关系.第(1)问通过独立事件的概率公式来分析与求解;第(2)问结合不同情况进行分类讨论,再利用独立事件的概率公式来分析与求解;(3)通过补集思想,借助对立事件与独立事件的综合应用来分析与解决.
解析:由题意知P(A)=0.8,P(B)=0.9.
(1)根据独立事件的概率,可知两人都射中的概率为P(AB)=P(A)P(B)=0.8×0.9=0.72.
在“三新”(新教材、新课程、新高考)背景下,进一步落实“双减”政策与新改革理念,积极贯彻《总体方案》要求,“概率”单元复习教学设计与安排在寻求基础、本质、能力、创新等的基础上,更多侧重数学基础与关键能力的考查,坚持开放创新与核心素养导向,更加注重数学创新意识与创新应用.

