“导数的概念”教学实录

上海中学东校 王 靓

1 教学目标设置

(1)经历用平均速度“逼近”瞬时速度的过程,体会瞬时速度的本质是平均速度的极限,初步体会极限思想;

(2)通过求自由落体运动中物体在具体时刻的瞬时速度,类比函数变化率的极限;

(3) 经历由特殊到一般,由量变到质变的过程,感悟数学抽象与逻辑的魅力.

2 教学重难点

教学重点：导数的概念和极限思想.

教学难点：从求瞬时速度的具体案例中抽象出导数概念.

3 学情分析

学生已经学习过瞬时速度,对瞬时速度有初步的描述性理解,但对于瞬时速度的算法比较模糊;同时,在高一年级函数零点的学习中,体会过利用二分法逼近函数的零点,学习过数列极限的描述性定义.现行的高中数学教科书在给出导数概念之前并没有严格介绍极限的概念及其运算.另一个认知障碍是对导数符号及其意义的理解,原因在于导数符号的高度抽象性.

4 教学过程设计

4.1创设情境

观看汽车时速、高铁时速、导航时速三个发生在我们身边的场景,提出问题1.

问题1当我们乘坐高铁时,常常会在车厢内看到如图1所示的列车信息显示屏.在列车运行中,显示的速度在不断的变化,说一说你对图中“速度350 km/h”的理解.

图1

生:我觉得是瞬时速度.

追问1：在物理学科中,相较于瞬时速度,你还学过什么速度?

生:平均速度.

追问2：物理中运动物体的平均速度和瞬时速度是如何定义的?

生:平均速度是运动物体的位移与时间的比值,瞬时速度是运动物体在某一时刻或某一位置的速度.

追问3：直觉告诉我们,“某一时刻”或“某一位置”是一个点,一个点的“位移”等于0.按照“常理”,“某一时刻的速度”应该都等于0,这与物体的运动状态相符吗?问题出在哪里?

生:运动物体在“某一时刻”或“某一位置”的时间也是0.

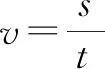
下面我们以自由落体为例来研究一下.

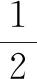
追问1：求t=2附近的时间段物体在t=1到t=3内的平均速度.

追问2：用20 m/s来表述自由落体运动中1至3秒的运动状态是否合理?

生:不合理.

追问3：为什么不合理?试着描述物体在t=1到t=3内的速度变化情况.

生：物体在1～3秒内的速度越来越快了.

设计意图：让学生发现用平均速度不能准确地反映自由落体物体的运动状态,仅用一个时间段内的平均速度难以准确描述在某时刻附近时间段内变速运动的过程,如何精确地对整个过程进行描述,引出研究瞬时速度的必要性.

追问4：能否用数据支持物体在1到3秒内的速度越来越快的结论?

生1:如果把这段时间分成[1,2]与[2,3]两段,那么在这两个时间段内自由落体的平均速度分别是15 m/s与25 m/s.

生2:如果以0.5 s为间隔把[1,3]分成4个时间段,可以得出这4个时间段内的平均速度分别是12.5 m/s,17.5 m/s,22.5 m/s,27.5 m/s.

师:随着时间段的不断细分,自由落体的物体运动状态得到了越来越精确的描述.

追问5：如何求自由落体运动中物体在t=2时的瞬时速度?瞬时速度与平均速度有什么关系?

生:用很短时间段的平均速度来近似得到瞬时速度.

师:事实上,物理实验中测量运动物体的瞬时速度确实是这样做的.物理实验中的光电门和打点计时器都是通过测量很短时间内的平均速度近似估计瞬时速度.

追问6：求物体在t=2时的瞬时速度,很短的时间间隔如何表述?你能举几个例子吗?

生1:[1,3],[1.9,2.1],[1.99,2.01],等等.

生2:[2,2.1] ,[2,2.01],[2,2.001],等等.

生3:可以取[2,2+t],然后对t的取不同的值,让其越来越小.

为了研究方便,我们在t=2之前或之后任取一个时刻2+h,将时间段记为[2+h,2](h<0)或[2,2+h](h>0).

设计意图：通过问题引导学生思考,从学生已知的平均速度出发,去探究未知的瞬时速度;通过缩短时间区间,用平均速度逼近瞬时速度的方法,培养学生分析、解决问题的能力.

对不同时间段长度值|h|,t=2附近时间段的平均速度如下:

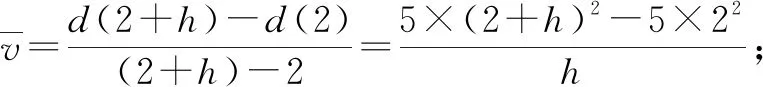
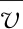
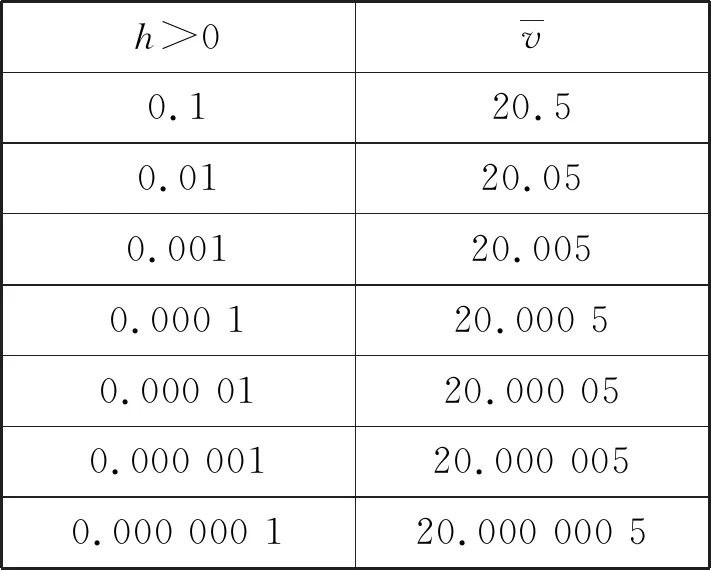
表1

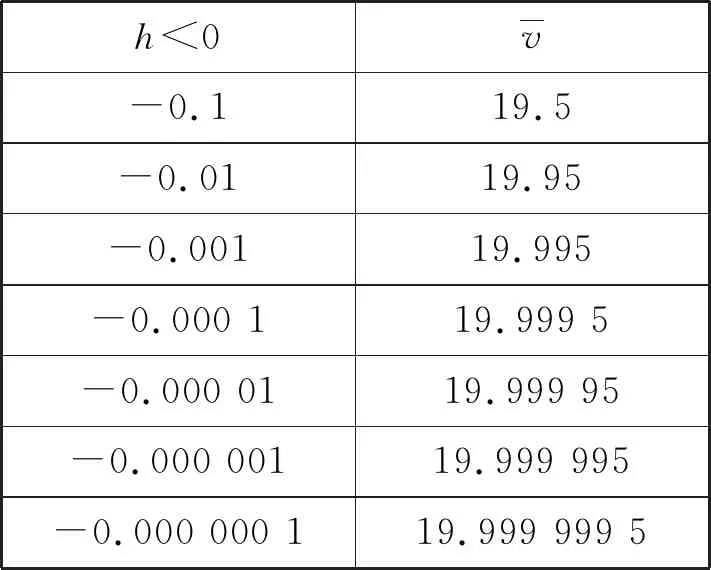
表2

追问7：观察表1,表2,能否给出自己的发现?

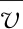
同一图形出现在连续几张课件中时，图形位置应固定不变，避免注意力的分散.体现了认知负荷理论的一致性原则.[19—21] 在课件播放过程中，学生比较容易关注动态的图形，位置发生改变，使相邻两页课件产生振动效果，不利于学生注意力的集中.勾股定理课件制作过程中，同一图形出现在连续几张课件中时，图形位置应固定，减少视觉对图形位置改变的处理，降低视觉产生的认知负荷.

追问8：你认为通过上述列表计算得出瞬时速度的过程可靠吗?可否用数学的计算与推理证实我们的判断?

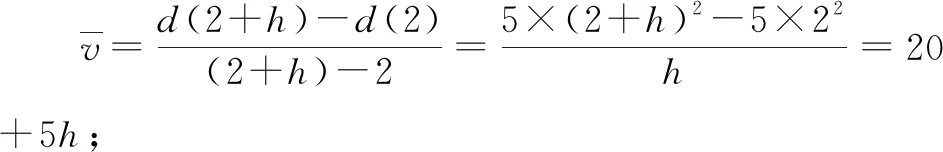
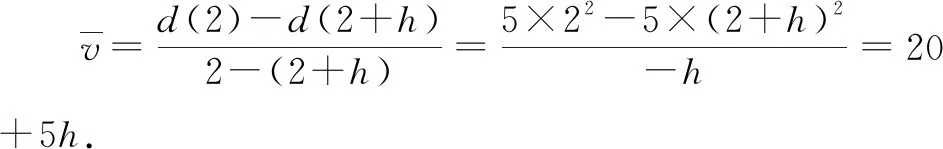
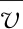
追问9：趋近一词是否用数学符号语言来表达?

生:可以用极限.

追问10：非常好!我们在数列的学习中学过极限,那么仿照数列的极限表达,你认为这里应该怎么表达呢?

生:可以将其表达为

师:很好,t=2时的瞬时速度就是这样表示.

设计意图：学生从表格直观感受逼近过程后,教师再引导学生利用运算来发现代数规律,渗透数学运算素养.数学是培养理性思维的重要载体,学习数学离不开运算推理和演绎证明.数学实验的结果需要用数学的运算推理加以验证,体现了理论与实践的统一,更让人信服.同时,培养学生崇尚数学的理性精神和审慎的思维习惯.

追问11：自由落体运动中,物体下落的距离d(单位:m)与时间t(单位:s)近似满足函数关系d=5t2.试求物体在t=1时的瞬时速度.

经过计算学生得出:t=1时的瞬时速度为

设计意图：期望学生通过类比,掌握表达式的结构,并加深对结构的认识,为下一步用字母表达数字做好铺垫.

追问12：我们已经计算出t=1 s,t=2 s的瞬时速度,那么对于某一时刻t=t0,你能计算出瞬时速度吗?

学生通过计算得出:

设计意图：从特殊到一般,通过运算求瞬时速度的过程,为抽象概括导数概念提炼出一个极限模型.

追问13：10t0与前面实验及证明的结论是否具有一致性?

生:代入t=1 s,t=2 s,发现与前面的结果一致.

追问14：10t0与物理学中自由落体运动的速度公式是否具有一致性?

生:物理中的自由落体速度公式为v=gt,其中g为重力加速度,近似取g=10 m/s2时结果一致.

设计意图：通过上述问题得到了自由落体运动在任一时刻t=t0处的瞬时速度为10t0,也就是自由落体运动在任意时刻t=t0处的导数.这说明导数是普遍存在的,可以在自由落体物体的任意运动时刻找到它.该过程体现了由特殊到一般、由具体到抽象的数学思想方法,为导函数概念的形成做好了铺垫.同时,通过数学运算得到的结论与学生熟知的物理中自由落体运动的速度结论一致,再一次让学生感受到数学作为基础学科的重要性.

4.2 抽象概念

问题3如何从数学角度对以上解决问题的方法进行更一般的描述?

追问1：如果研究更一般的问题,函数y=f(x)在x=x0的瞬时变化率如何表示?

追问2：根据导数定义,你能用导数来重述自由落体运动问题的结论吗?

生:自由落体运动物体在t=2时的瞬时速度就是其下落距离d(t)在t=2时的导数值,即为d′(2).

4.3 例题讲解

例1已知在使用某种杀菌剂t小时后室内的细菌数量为f(t)=-103t2+104t+105.

(1)求f′(10);

(2)f′(10)的实际意义是什么?

解：(1)当h≠0时,在使用杀菌剂10小时附近的时间段[10+h,10](h<0)或者[10,10+h](h>0)内,细菌数量关于时间的平均变化率为

=-104-103h.

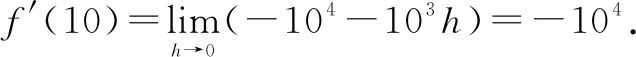
(2)f′(10)的实际意义是细菌数量在t=10时的瞬时变化率.它表明在t=10附近,细菌数量大约以每小时104的速率减少.

思考：能否求出t=t0时的f′(t0)?

设计意图：此例题为教材中的例1,但将教材中f(t)=105+104t-103t2改为f(t)=-103t2+104t+105,这样书写更规范,更有利于学生计算.虽然本题的运算量较大,但未对具体数据进行优化,主要原因有两个方面.一是考虑在未来科学研究中的数据大多是繁复的,二是一定量的运算是提升学生运算素养的训练.

练习1将原油精炼为汽油、柴油、塑胶等各种不同产品,需要对原油进行冷却和加热,已知在第x小时时,原油的温度(单位:℃)为f(x)=x2-7x+15(0≤x≤8).经过计算可知f′(2)=-3,f′(6)=5.试说明它们的意义.

练习2阅读下列情境,并尝试用自己的语言解释相应导数的实际意义:

(1)竖直向上发射的火箭熄火时的上升速度为100 m/s,此后其位移H(单位:m)与时间t(单位:s)近似满足函数关系H(t)=100t-5t2,H′(2)=80;

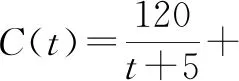
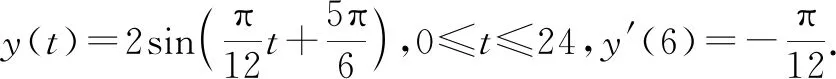
追问：根据导数定义,你能用导数来解释复兴号列车显示屏上的350 km/h的意义吗?

生:复兴号列车在8∶03那一瞬间的瞬时速度是350 km/h,也就是列车的位移关于时间的函数在那一时刻的导数值是350.

师:复兴号是我国自主研发的具有独立知识产权的新一代高速列车,2022年北京冬奥会的复兴号专列成为了一张国家名片,冬奥会期间各国的记者和运动员搭乘“瑞雪迎春”复兴号感受到了中国速度与冰雪激情.

设计意图：《微积分的力量》一书中写到,我们不必为了理解微积分的重要性而学习如何做运算,就像我们不必为了享用美食而学习如何做佳肴一样,在导数概念的第一课时中,理解导数的概念及意义更重要,而学会求导以及如何计算不是本节课的教学重点.同时,通过以上物理、化学、生物、地理中的实例感受导数主要用来刻画运动和变化,以及微积分在自然科学及社会科学中的广泛应用,深入体会“数学是一切科学的语言”.

4.4 数学文化

师:这节课中,由物理中的瞬时速度抽象出导数概念的这一过程,历史上第一个发现的人是牛顿.1666年英国伦敦突发鼠疫,牛顿所在的剑桥大学也被迫封校,牛顿被隔离在乡下的家中,潜心研究,才有了这样震惊世界的发现,世人都称牛顿为居家隔离型的天才少年,所以大家即使被疫情所扰,一旦被隔离在家,也不用过分担心,如果潜心研究,说不定这是一次改变世界的机会.

设计意图：简述牛顿从物理学的角度发明微积分的故事,另一位发明人莱布尼茨是从数学角度发明了微积分.要求学生上网查询相关历史.

4.5 课堂小结

通过一种现象——从“平均变化率”到“瞬时变化率”:

利用一种运算——极限;引入一个概念——导数.

从而使一个难以描述的问题得到了准确的数学表达,以此为根基建立了整个微积分的大厦.

4.6 拓展思考

扫码看授课视频

②f(x)=|x|,x0=0.

5 教学体会与思考

概念课要舍得花时间让学生细细体会概念的发生、发展过程,品味概念生成的每一个环节实则对学生的创新意识及审慎思辨的态度的影响是深远的.结合课例,笔者认为概念课要做到以下三点.

5.1 选择恰到好处的情境

5.2 提出促进思维的问题

问题指引着数学学习的基本方向,数学的基本知识、基本思想方法及数学解题策略都是基于一系列的问题产生的.

本节课教师在自由落体问题的探究过程中利用“问题串”串起研究的必要性(追问1-4)、如何展开研究(追问5-6)、研究过程(追问7-11)、研究结论(追问12)以及研究结论正确性论证(追问13-14)的过程.通过14个问题引领学生展开具有深度的思维活动,问题由浅入深,逐渐提升问题层次,最终深入数学的本质.教师提出问题的质量决定了教学的质量与效率,所以设计合理的“问题串”引导学生进行基于思维的自主探究,是教师“润物细无声”的亲身示范,是教师对学生进行数学抽象素养渗透的良好时机.

5.3 遵循数学抽象的过程

从教学过程来说,教师在概念课的课堂教学中的抽象过程遵循了实物层面的抽象(自由落体运动在2 s处的瞬时速度)—初步概括的抽象(瞬时速度到瞬时变化率抽象)—符号层面的抽象(导数的概念及导数符号语言的理解)—系统化层面的抽象(基于导数定义及导数实际意义理解的例1及练习1,2)这一过程,教科书中的抽象过程是生硬的没有过渡的,而课堂教学的优势就是教师用丰富的教学行为将各抽象之间的过渡衔接得更加符合学生的认知能力.

在课堂教学中,教师要用自己的行为为学生做出良好的示范及引导,潜移默化地发展学生分析、解决问题的能力,将数学抽象素养的培养落实在教学行为中.基于数学抽象素养培育的教学实践研究一直在路上,期待更多教师不断地探索、实践、交流.