从不同教科书看直观想象素养的渗透——以基本不等式为例

西华师范大学数学与信息学院 李晓丹

基本不等式是高中阶段不等式学习的核心内容和重要节点,具有承上启下的作用[1].从数学素养的角度来看,基本不等式的学习过程中蕴含着多种核心素养.首先,提到基本不等式我们就会想到数学运算和逻辑推理素养,因为与不等式有关的题目基本上都要运用计算或证明.其实,基本不等式的学习中还蕴含着其他数学核心素养,比如,从情境中抽象出基本不等式要用到数学抽象素养、提炼基本不等式的几何意义时要用到直观想象素养,等等.基本不等式的抽象性导致不少学生产生了畏难情绪,而直观想象素养可以化抽象为直观,帮助学生理解基本不等式,从而降低学习难度.因此,直观想象素养在基本不等式学习中非常重要.

《普通高中数学课程标准(2017年版)》(以下简称《课程标准》)指出,直观想象是借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形理解和解决数学问题的一种素养[2].从课程标准可以看出,直观想象包含两点,分别是几何直观与空间想象.几何直观是借助图形清晰直观地描述和分析数学问题,从而使复杂问题简单化,抽象问题具体化,进而解决问题的能力.空间想象是直接通过感知去理解图形及其性质的能力.直观想象主要表现在四个方面:(1)建立数与形的联系;(2)借助几何图形描述问题;(3)借助几何直观理解问题;(4)运用空间想象认识事物[3].

下文将对基本不等式在人教A版、人教B版、苏教版三个版本教材中的呈现方式进行分析,讨论不同教科书中直观想象素养的渗透方式及异同点.

1 教材分析

1.1 人教A版

基本不等式位于人教A版必修一第二章第二节.

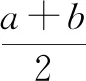
图1 人教A版必修一第45页书影

该版本在例题与习题部分通过基本不等式的实际应用培养学生的直观想象素养:让学生从实际问题中抽象出图形,训练几何直观能力;让学生通过各图形的性质找出周长与面积的关系,训练空间想象能力.

1.2 人教B版

基本不等式在人教B版中称为均值不等式,位于必修一第二章第二节“不等式”中.

这一版本中,教材先建立了几何平均值的图形联系,接着探究几何平均值和算术平均值的几何意义,在此基础上得出了基本不等式的几何意义,环环相扣,层层推进.在本节最后的“探索与研究”环节,给出帕普斯的半圆模型,让学生自主探究基本不等式的另一种几何意义,如图2所示.这将进一步加深学生对基本不等式的理解和记忆.B版给出的两种几何意义,充分渗透了直观想象素养.

图2 人教B版必修一第73页书影

人教B版在例题与习题部分与人教A版相似,也是通过实际问题,如“菜地的周长和面积”来引导学生发展直观想象素养.

1.3 苏教版

苏教版的基本不等式位于必修一的第三章的第二节中.

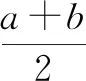
图3 苏教版必修一第51页书影

2 对比分析

2.1 引入

几何图形可以激发学生的直观想象素养[7].三个版本教科书为了在基本不等式的学习中渗透直观想象素养,均设置了一些带有几何特点的情境引入(见表1).人教A版教科书选择了赵爽弦图,“弦图”不仅结构简洁优美,还具有数学文化的特点,能够体现数学学科的育人价值.人教B版采用矩形引入,矩形作为学生最熟悉的图形方便学生理解和迁移.苏教版采用实际情境引入,不仅直观还具有趣味性.

表1 不同版本教科书中基本不等式的引入方法

2.2 证明

各版本教材都对基本不等式从几何角度进行了证明,即通过图形动态地展示基本不等式从“不等”到“相等”的过程[8].从几何角度证明不等式,有两种方法:一是直接给出几何图形,根据图形做出基本不等式的几何解释(根据图来证明);另一种方法则是不给出图形,让学生自己构造图形进行证明.纵观各个版本教科书,均直接给出几何图形让学生利用几何图形去验证基本不等式(见表2),并没有出现让学生构造几何模型去验证基本不等式,可能是考虑到这种要求对于学生来说还是很难达到的.各版本教科书给出的图形基本是帕普斯半圆模型,但不同的教科书在使用半圆模型时也略有区别.比如,人教A版中,没有给出半径,只是给出了半弦,此时还需要学生去构造出半径,增加了难度.

表2 不同版本教科书中基本不等式的几何证明方法

2.3 例题与习题

直观想象核心素养的培养依赖于数学问题[9],因此例题和习题对于培养学生的直观想象素养发挥着不可或缺的作用.例习题方面,三个版本教材均设置了一些几何问题让学生借助图形进一步理解基本不等式.不管是人教A版、B版还是苏教版,几乎所有例题习题都需要学生发挥几何直观能力和空间想象能力将数与形相联系,借助图形解决问题.这一过程不仅加强了学生对基本不等式的理解,还有助于培养学生的直观想象素养.在苏教版的习题中还出现了赵爽弦图,这进一步体现出了赵爽弦图的重要性.总之,各个版本在例习题上差别不大,都设置了几何问题,帮助学生巩固基本不等式,发展直观想象素养.

通过对各版本教科书的研究,可以发现直观想象素养贯穿了基本不等式学习的各个环节(不等式的引入、不等式的证明、习题巩固).教科书的设计在结合学生认知规律的同时,还为不同层次学生直观想象素养的发展提供了平台,为学生直观想象的发展营造了氛围,创造了契机.

直观想象是数学思维能力在解决问题中的重要体现,凭借直观想象可以培养学生的数形结合能力,实现化抽象为具象,从而有效降低知识的难度,使学生认知和理解数学知识的本质,进而促进学生理性认识的生成,使学生体会到数学的价值[10],最终实现“学生爱上数学”的目的.虽然直观想象素养的概念是相同的,但是各个版本在其体现方式上有所不同,所以教师使用教材时应多对比,取众家之长.本文中通过比较各个教材对于基本不等式的呈现方式,发现各版本教材在培养学生直观想象素养上都有其不同的特色和优势,教师在教学中可以借鉴其他版本教材内容,丰富学生课堂体验.比如,学习基本不等式时,苏教版可以引入人教A,B版的几何解释来发展学生直观想象素养.