关于区间Opial型不等式的进一步推广

连俊勤, 赵大方

(湖北师范大学 数学与统计学院,湖北 黄石 435002)

0 引言

1960年,波兰数学家OPIAL Z[1]建立了积分不等式:假设f∈C1[0,h],满足f(0)=f(h)=0,且f(x)>0对任意的x∈(0,h)都成立,则

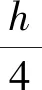
此后,Opial不等式便引起了国内外学者的广泛关注,BEESACK P R、华罗庚、AGARWAL R P、赵长健等对Opial不等式进行了不同形式的推广[1-6]。由于Opial不等式在微积分和微分方程等领域的重要应用,至今仍是不等式研究领域的一个热点。最近几十年,国内外学者对Opial不等式及其应用进行了广泛的研究[7-11],在连续型推广、离散化推广以及右端系数的精确估计等方面取得了丰硕的成果,Hermite-Hadamard 型[12]不等式等亦取得了很好的成果。近些年,区间分析作为一种解决不确定性问题的新方法得到了广泛的应用,而区间积分理论是区间分析的重要组成部分。2012年以来,一些经典的积分不等式,诸如Ostrowski不等式[13]、Beckenbach不等式[14]、Chebyshev不等式[15]等已经被推广至区间值函数的形式。2019年,COSTA T M等人[16]建立了区间Opial型不等式,得到了一些富有意义的结果,但其主要结论中对不等式右端系数的估计并不是最佳的。2022年,ZHAO D F等人[10]对文献[16]中的区间Opial型不等式进行了进一步的推广。在基于文献[10]和文献[16]的研究基础上,笔者对区间Opial型不等式进行了进一步的改进与推广,得到了一些新的结论。所得结论不仅改进了已有区间Opial不等式右端系数的估计,也为区间微分方程、区间差分方程以及模糊区间不等式等相关问题的解决提供了研究工具。

1 预备知识

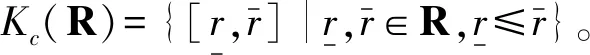
AӨB=C⟺A=B+C,

即对∀A∈Kc(R),有AӨA=[0,0]。但对于Kc(R)中任意两个不同的区间,其H-差不一定存在。为解决这个问题,2009年,STEFANINI L等[18]引入了gH-差,

即gH-差对Kc(R)中任意A,B都成立,有

显然,(Kc(R),d)为完备的度量空间,其中,d为Kc(R)上的Hausdorff度量,即对∀A,B∈Kc(R),有

此外,易知(Kc(R),+,·)为拟线性空间,其中拟范数=·=为

有关区间值函数连续、单调、μ-增和[A]μ的概念可参看文献[10],切换点和gH-可导的概念可参看文献[18]。

2 关于区间Opial型不等式的进一步推广

定理1设P,Q:[s,t]→R是[s,t]上的实值绝对连续函数,μ1,μ2≥1。

1)如果P(s)=Q(s)=0,则

(1)

2)如果P(s)=P(t)=Q(s)=Q(t)=0,则

(2)

其中k=max{μ1,μ2}。

证明1)当u1=u2=1时,由文献[4]中的定理2.14.1,有

当u1≥2,u2≥2,P(s)=Q(s)=0时,有

从而有

因此,有

同理可得

即证(1)式。

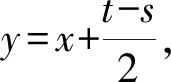
从而即证(2)式。

注记1在(1)式中,当P(x)=Q(x),μ1=μ2=1,s=0,t=b时,(1)式退化为

(3)

(3)式为文献[2]中的公式(3);当P(x)≠Q(x),μ1=μ2=1时,(1)式退化为文献[16]中的推论4.1,

(4)

当P(x)=Q(x),μ1=μ2=1时,(1)式退化为文献[16]中的推论4.2,

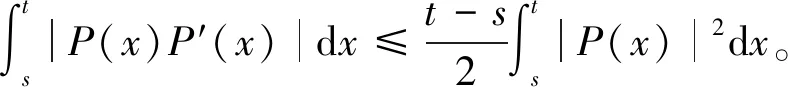
(5)

(5)式是(3)式的推广,(4)式是(3)式与(5)式的推广。

在(2)式中,当P(x)=Q(x),μ1=μ2=1,s=0,t=b时,(2)式退化为

(6)

(6)式为文献[2]中的公式(1);当P(x)≠Q(x),μ1=μ2=1时,(2)式退化为

(7)

当P(x)=Q(x),μ1=μ2=1时,(2)式退化为

(8)

(8)式是(6)式的推广,(7)式是(6)式与(8)式的推广。

注记2当μ1=1,μ2=4时,与文献[10]中(3.8)式计算出来的123.66相比,49.68显然更为精确。

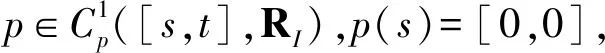
(9)

证明根据拟范数的定义,有

由文献[10]中的引理3.1,有

再根据定理1的(1),有

从而有

即证(9)式成立。

注记3当(9)式中的u1=u2=1时,(9)式退变为文献[16]中的定理5.2,

(10)

同样,下面的定理3是文献[16]中定理5.3的推广。

例2设

为逐段连续可微的区间值函数,当μ1=2,μ2=1时,可得

注记4例2计算所得的39.41显然比文献[10]中(3.10)式计算出来的43.58更为精确。

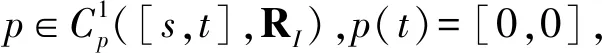
(11)

证明定理3的证明与定理2的证明类似,故省略。

注记5当(11)式中的u1=u2=1时,(11)式退变为文献[16]中的定理5.3,

(12)

而下面的定理4则是文献[16]中定理5.4系数估计的改进。

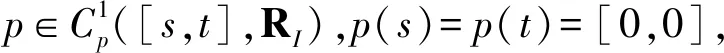
(13)

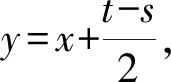
注记6当u1=u2=1时,(13)式退化为

(14)

显然,(14)式与文献[16]中定理5.4的不等式

(15)

相比,显然更为精确。

当(14)式中的s=0时,(14)式退化为

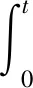
(16)

显然,(16)式与文献[16]中的定理5.1的不等式

(17)

3 结论

本文主要研究了区间Opial型不等式,改进了一些单变量的区间Opial型不等式,为今后研究多变量的区间Opial型不等式,以及为不等式提供一种新的系数估计做了一些基础性的工作。