空间三角形重心的判定条件和算法

张 辉, 方晓峰, 郑丽娜

(火箭军工程大学 基础部,陕西 西安 710025)

0 引言

空间三角形的五心重心、内心、垂心、外心和旁心,是空间解析几何中重要的知识点。如何判定某点是空间三角形的五心是一个较为复杂的问题,而能否通过空间三角形3个顶点的坐标确定五心坐标的解析表达式也是值得关注的问题。本文主要针对空间三角形的重心问题,利用向量代数相关知识研究重心判定的充分必要条件,进而得到空间三角形重心坐标的表达式和相关性质。

1 两个引理

为了研究空间三角形[1-2]的重心问题,首先给出以下两个重要的关于空间三角形内点的引理。

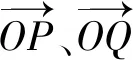
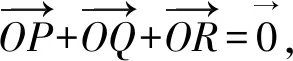
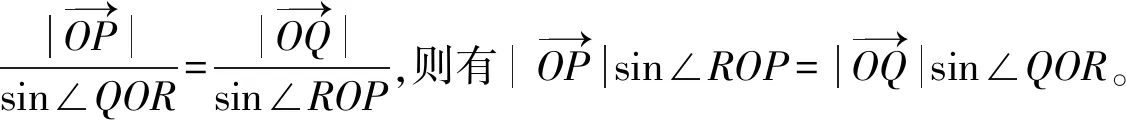
因为

和

则有

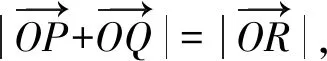
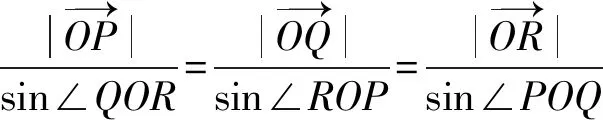
利用引理1的结论,可以得到引理2。

引理2设点O为空间ΔABC的任意一个内点,则有

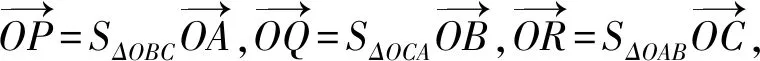
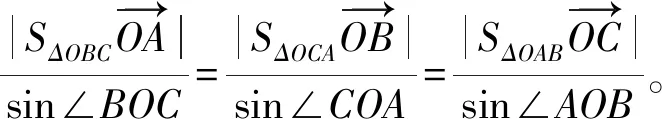
sin∠BOC=sin∠QOR,sin∠COA=sin∠ROP,sin∠AOB=sin∠POQ,

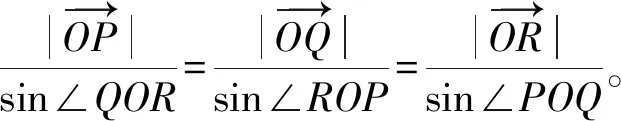
2 重心的判定条件和计算

由三角形面积的性质,可得命题1。

命题1若点O为空间ΔABC的重心(图1),即点O为3条中线AD、BE和CF的交点,则有

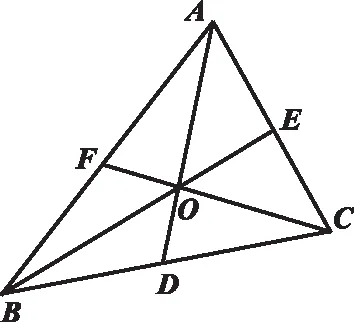
图1 空间三角形的重心

和

利用引理2和命题1,下面研究并给出判定空间一点是空间三角形重心的充分必要条件。

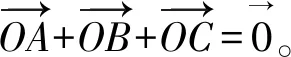
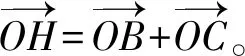
事实上,利用定理1也可以得到判定重心的另一个充分必要条件。

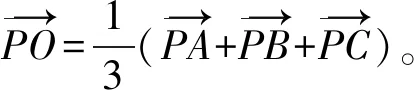
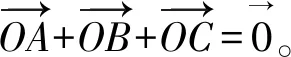
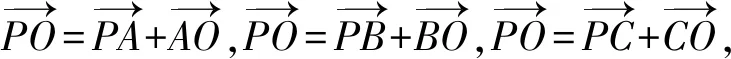
事实上,在定理2中若取点P恰好为重心O即为定理1。因此,定理1是定理2的特殊情形。同时定理1和定理2不仅分别给出了一个判断空间一点是空间三角形重心的充分必要条件,而且分别提供了一种求重心坐标便捷有效的方法。

设空间三角形ΔABC3个顶点的坐标分别为A(x1,y1,z1)、B(x2,y2,z2)和C(x3,y3,z3),记重心为O(x,y,z),若取点P为空间直角坐标系的原点,由定理2可得

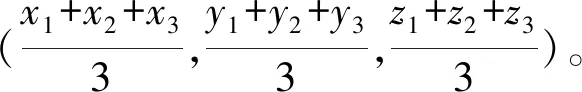
特别地,在定理2中若取点P分别为顶点A、B和C,则有以下定理3。

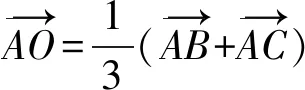
值得注意的是,借助于重心O的坐标,可以计算

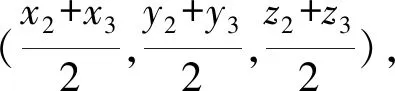
即OA=2OD。同理可得OB=2OE和OC=2OF。也就是说,空间三角形的重心到某顶点的距离是到该顶点对应边的中点的距离的2倍。事实上,这个结论和定理3的结论是一致的。

3 结语

本文研究了空间三角形重心的判定条件和计算问题,得到了判定重心的3个充分必要条件,并利用判定条件给出了空间三角形重心坐标的计算公式,旨在让学生对空间三角形的重心有更深入的理解和掌握,为空间三角形在工程技术领域[4-7]中的应用提供技术支撑。值得注意的是,平面三角形关于五心的研究已经有了许多优美的结论[8-10],而空间三角形与五心有关的计算结果会与之不同,进而丰富了空间解析几何[11-14]的内容体系。