常数项级数的若干种求和方法

赵莉莉

(云南大学 数学与统计学院, 云南 昆明 650091)

0 引言

无穷级数是用来逼近较复杂函数的有效工具,能够解决大量的实际问题,是微积分学的重要组成部分,也是历年考研中的重点与难点。它有两种主要的运算,其一为求无穷级数的和[1-3],其二为将函数展开成幂级数。熟练掌握求无穷级数,尤其是求常数项级数和的各种基本方法,是理解并运用无穷级数理论的基础,因此,有必要汇总常数项级数的求和方法。

1 利用已知级数求未知级数的和

常数项级数的和等于其部分和数列的极限,因此需要将部分和数列向易于求和的数列(如等比数列与等差数列)转换,以便求出部分和数列的极限。

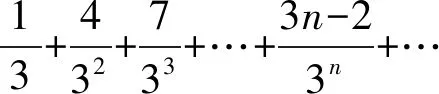
解分母为等比数列,分子为等差数列的常数项级数求和,一般使用错位相减法。

故,

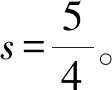
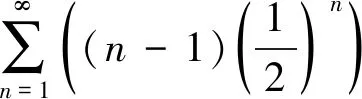
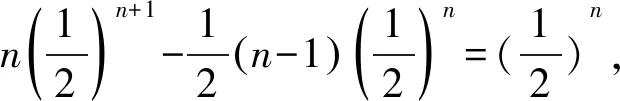
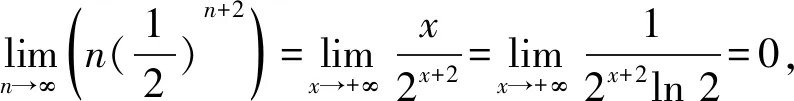
2 连锁消元法

所谓连锁消元法就是巧妙利用公式,将常数项级数部分和数列的中间项消去,只剩下第一项与最后一项,以便求出极限。

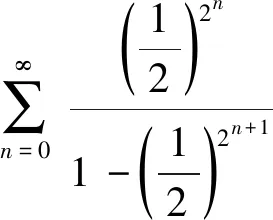
解

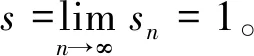
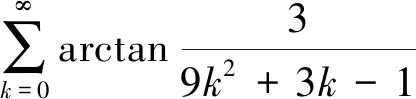
(1)

与

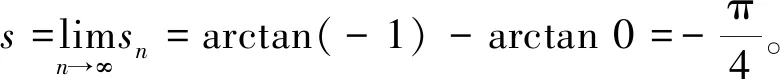
连锁消元法还可以多项相消,如例5。

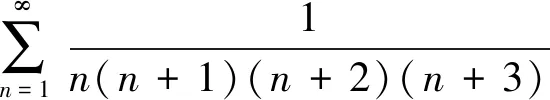
解考虑到常数项级数一般项的分子是一个常数,为了将部分和数列的中间项消去,不妨先将一般项改写为

从而

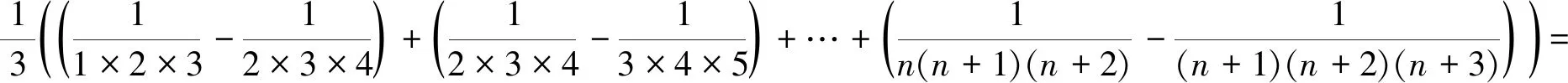
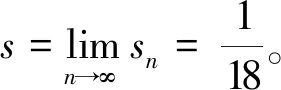
3 子序列法

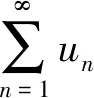
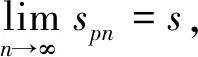
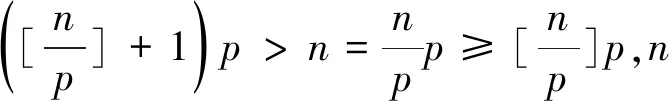
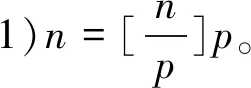
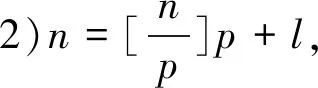
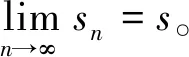
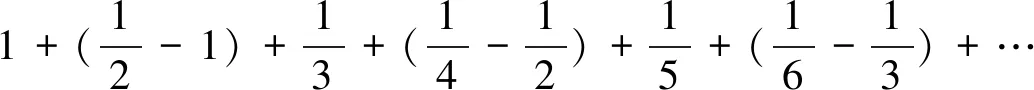
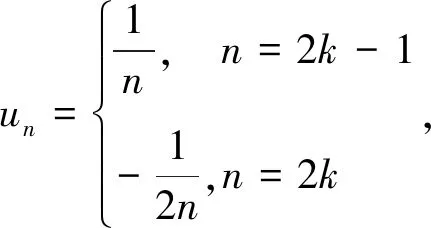
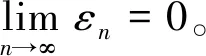
故原级数的和s=ln 2。

4 建立关于sn的关系式,以便求出sn及其极限

例7计算psinα+p2sin (2α)+…+pnsin (nα)+…(|p|<1)的和s。

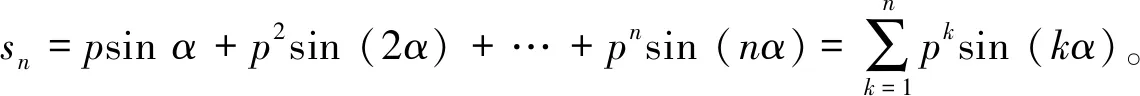
pn+1sin((n+1)α)+sn-psinα+p2sn-pn+2sin (nα)。

整理后,有

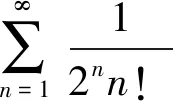
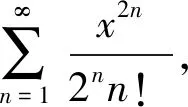
5 利用定积分的定义

这种方法的要点是先求出常数项级数的部分和数列,再将部分和数列改写为定积分定义中的和式形式。

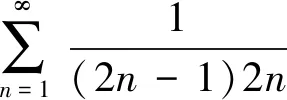
解先求常数项级数部分和数列的通项,可得

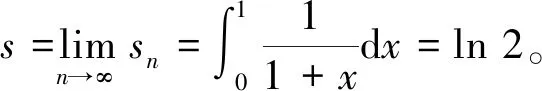
6 利用部分和函数序列的紧缩形式

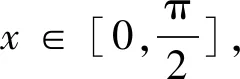
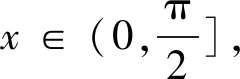
于是

(2)

利用Riemann引理[5-9],当n→∞时,(2)式第一项趋于零,故