论四维弯曲时空中的正则方程及量子力学原理

李宜和

(河南财政金融学院 计算机与人工智能学院,河南 郑州 450046)

0 引言

在分析力学中,既可以从变分原理的微分形式即虚功原理出发,推导出拉格朗日方程及哈密顿原理,也可以从积分形式的哈密顿原理出发推导出拉格朗日方程及正则方程,而用泊松括号表示的正则方程又与量子力学中的海森堡方程有密切关系[1]。上述理论在经典力学及电动力学中都是成立的[2]。于是,一个新的问题自然而然地产生了:在四维弯曲时空中,这些原理是否成立?既然牛顿运动定律及带电粒子在电磁场中的运动定律都可以由哈密顿原理推导出来,那么弯曲时空的测地线方程也可能会从哈密顿原理推导出来。根据广义相对论,牛顿引力论只是广义相对论在弱场低速极限下的一种近似理论[3],若是把弯曲时空中的度规张量gμν变成ημν(μ,ν,λ,σ=0,1,2,3),则四维弯曲时空就变成了四维闵氏平直时空。无论是引力场中的牛顿运动定律,还是四维闵氏平直时空的带电粒子,在电磁场中的运动定律都可以由哈密顿等时变分原理得出,我们完全相信,从哈密顿等时变分原理出发一定会得到四维弯曲时空的测地线方程﹑拉格朗日方程及哈密顿正则方程。

当然弯曲时空的测地线方程已经由爱因斯坦利用哈密顿原理推导出来[4],但在推导过程中他没有采用等时变分原理,而是把三维变量推广到四维变量,然后将作用量对任意变分参数进行变分。虽然得到了测地线方程,但没有给出弯曲时空中的拉格朗日方程及正则方程。

本文首先根据等时变分原理,推导出四维弯曲时空的3个测地线方程,这3个方程只是测地线方程的一部分,同时证明它与推导得到的测地线方程是一致的,并给出弯曲时空的哈密顿函数及正则方程。定义广义四维动量并给出完整的测地线方程,此方程与广义相对论中的测地线方程是一样的。最后,给出弯曲时空中一般形式的矩阵力学方程,并将它应用到静态球对称时空中,最后进行了总结与展望。

1 等时变分原理与测地线方程

故

(1)

其中x0=ct,i,j,k,=1,2,3。

根据等时变分原理,

(2)

为计算方便,将L展开,则

(3)

在A,B处,δxi=0。经过整理得

(4)

变分原理要求(4)式为零,则

(5)

即

(6)

此为四维时空测地线方程,但公式(6)只是测地线方程的一部分,下面将继续推导其完整的表达式。

2 拉格朗日方程

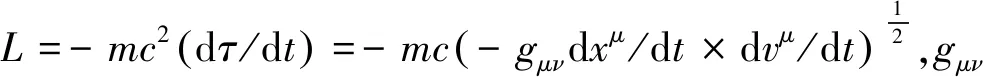
即

(7)

而

(8)

(9)

将式(8)和式(9)代入式(7)就得到方程(6)。

3 正则方程[1]

(10)

(11)

(12)

故

(13)

(14)

(15)

结合公式(6)和(14)得

(16)

则

(17)

公式(17)即为四维弯曲时空的测地线方程[5-6]。需要注意的是,根据勒让德变换[1],哈密顿量H不再是pi的函数,而是pi的函数。

4 球对称静态时空的量子矩阵力学

前面详细讨论了弯曲时空中的测地线方程以及正则方程。由于gμν的复杂性,使一些问题变得非常复杂,但在一般的实际应用中,很多时候以球对称静态时空为研究对象,其线元为ds2=-g00c2dt2-giidxidxi,则

(18)

5 总结与展望

在量子力学建立的过程中,海森堡为了解决玻尔理论存在的问题,从哈密顿正则方程出发,推导出量子矩阵力学。那么,为了得到四维弯曲时空中的量子矩阵力学,就必须知道四维弯曲时空中的正则方程,而正则方程的获得一般是通过变分原理。虽然爱因斯坦也从变分原理出发,得到了四维弯曲时空中的测地线方程,但由于他把时间分量看成独立的变量,因而并没有得到相应的正则方程。本文按照等时变分原理严格推导出四维弯曲时空中粒子的运动学方程,即测地线方程,进而推导出拉格朗日方程及正则方程,从而得到四维弯曲时空中的拉格朗日函数﹑哈密顿量等。在此基础上,根据相对论性量子矩阵力学,进而得到了四维弯曲时空中的量子矩阵力学。最后将这些结论运用到静态球对称空间,从而得到相应的动力学方程及量子矩阵力学方程。

虽然得到了正则方程﹑哈密顿量及矩阵力学方程,但并没有得到波动力学方程,因而下一步研究是推导波动力学方程的表达形式。但波动力学方程必须与本文的一些结论相一致,比如哈密顿量中的动量一定是广义动量而不是机械动量;波动力学也一定要与量子矩阵力学相一致:根据哈密顿算符及矩阵力学得到的物理量算符之间关系,一定要与广义相对论中物理学量之间的关系相一致。对于推导哈密顿量的算符表达式,这些都具有指导意义和启发作用。