放气活门用金属膜盒压力-位移特性

李 肖, 满春雷, 曹 洋, 尹文龙, 张 晋,3

(1.中国航发长春控制科技有限公司, 吉林 长春 130102; 2.燕山大学 机械工程学院, 河北 秦皇岛 066004;3.河北省重型机械流体动力传输实验室, 河北 秦皇岛 066004)

引言

金属膜盒组件具有良好的压力-位移特性,广泛应用于信号检测、密封和振动抑制[1-6]。放气活门是航空发动机中的重要组件, 主要作用是放掉压气机出口的部分空气以防止发动机喘振[7]。某型航空发动机采用金属膜盒组件作为放气活门的压力敏感元件[8],如图1所示。因此,研究膜盒组件的位移特性和压力响应对航空发动机的控制尤为重要。

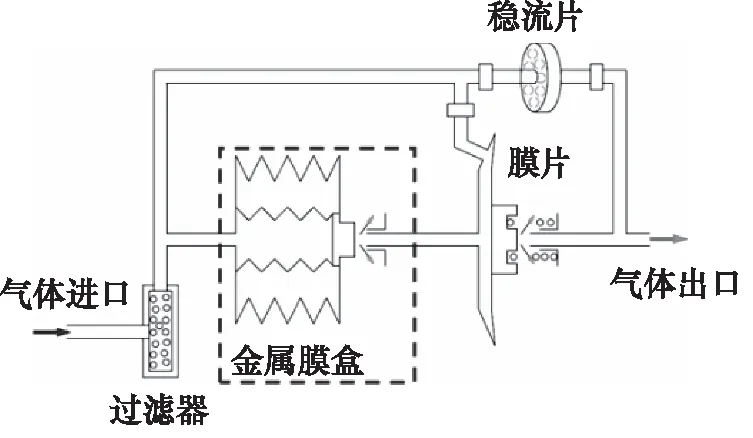
图1 放气活门控制气路原理图Fig.1 Schematic diagram of control gas circuit in vent valve

金属膜盒作为重要的机械式弹性敏感元件,机械结构、加工工艺和材料参数对膜盒性能的提高至关重要。王战生等[9]设计了一种膜盒式压比敏感元件,相比分压器式压力比测量元件,具有结构紧凑、控制精度高和性能稳定等优点;余锋等[10]分析了膜盒的疲劳断裂机理,得出膜盒内焊缝存在明显的应力集中,通过增大初始压缩量的方式使膜盒的疲劳寿命提高3倍以上;毕监勃等[11]提出了一种新的热处理方法,弥补了膜盒高压侧压力响应不足的缺陷;杨富丽等[12]通过对AM350钢与3J53恒弹合金性能进行对比,发现AM350比3J53有更高的强度和硬度,通过振动试验验证了膜盒的抗振性能;黄特伟等[13]研制了一种Nb合金应用于膜片膜盒,提高了膜盒的耐腐蚀性、弹性性能和疲劳性。

膜盒的性能是影响膜盒应用的主要因素,国内外相关学者基于试验与数值模拟的方式对膜盒的性能做出了预测。PIAO Changhao等[14]通过试验和有限元的方法对膜盒的弹簧常数进行了预测;王亚军等[15]采用有限元分析法对膜盒不同压力下的拉伸、压缩刚度值进行了预测,结合Abaqus非线性屈曲法对膜盒柱失稳临理论计算式进行分析,得到一种膜盒内压柱失稳临界压力值计算方法,通过试验验证了方法的适用性;史淑娟等[16-17]针对膜盒在气压作用下相邻膜片的贴合,基于ANSY的接触对膜盒出现接触时的刚度进行了分析,并考虑膜盒和外界流体的流固耦合,对膜盒进行了动力学分析;GHENI M等[18]对不同波纹管膜数和加载条件下膜盒的刚度和柔性进行了分析,并得出膜盒膜数与位移、应力、柔度的关系;高阳等[19]设计了一种基于单片机控制的自动测试系统对膜盒特性进行检测;SI H H等[20]对单层和双层高参数膜盒机械密封的抗扭强度进行了数值模拟,得到了应力-应变图,并通过试验进行了验证;王太平等[21]基于ABAQUS结构仿真软件对膜盒的充放气过程进行了模拟分析,得出适当的增大限位行程、避免膜片组校型可提高金属膜盒疲劳寿命。刘锦凡等[22]基于气液接触面的力平衡条件和流量连续性方程,推导了考虑膜盒机械刚度的蓄压器动力学模型,分析了膜盒刚度对POGO稳定性的影响。

以上分析结果表明,国内外相关学者对膜盒结构、工艺及其性能分析方面做出了大量的研究。本研究通过对膜盒的工作原理分析,建立膜盒压力-位移的数学模型,通过有限元仿真对膜盒膜片应力应变进行分析,建立膜盒在压比控制下的压力-位移关系,最终,通过试验建立了膜盒出程和回程的压力-位移关系,验证了理论与仿真结果的可信度。

1 金属膜盒及其工作原理

1.1 金属膜盒

放气活门金属膜盒组件由端头、通气限位柱、小膜片、大膜片、底座组成,如图2所示。其中,大小膜片组成的中间腔为真空状态,通气限位柱的作用是疏导控制气体、限制膜盒高度,底座的作用是固定膜盒。

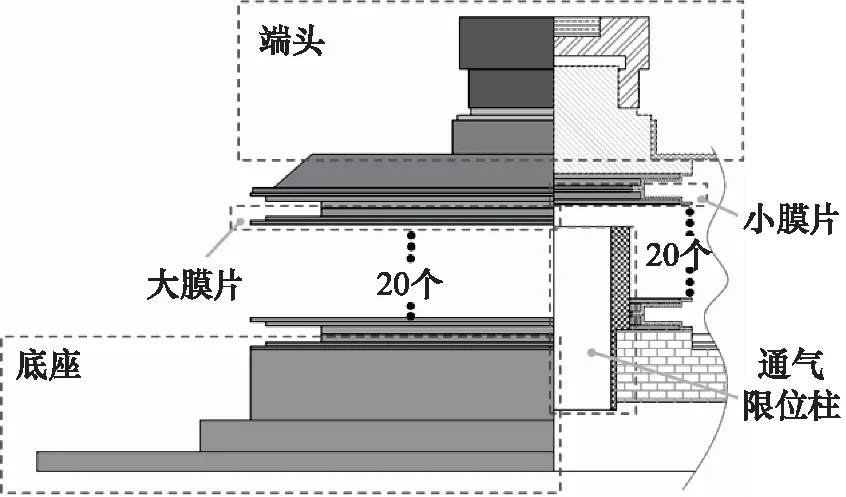
图2 膜盒结构示意图Fig.2 Schematic diagram of diaphragm bellow structure

1.2 膜盒理论数学模型

膜盒在工作过程中受到环境压力p0、中间压力p1和控制压力p2的作用,膜盒的受力状态如图3所示。大膜片外侧受到环境压力p0的作用,小膜片外侧受到控制压力p2的作用,在大膜片和小膜片之间为中间压力p1。环境压力作用面积大于控制压力作用面积,所以在控制压力等于环境压力时膜盒处于压缩状态。

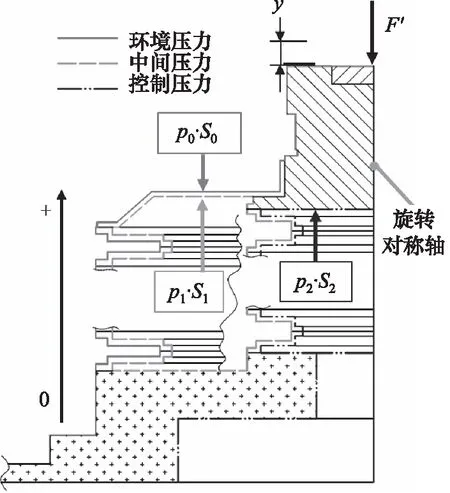
图3 膜盒受力状态图Fig.3 Stress state diagram of diaphragm bellow

由图3可得,环境压力p0作用在膜盒上部时,使膜盒压缩;环境压力p0和中间压力p1共同作用在大膜片,使膜盒压缩;控制压力p2与中间压力p1作用在小膜片时,使膜盒压缩;控制压力p2作用在内腔顶部时,使膜盒伸出。以作用在小膜片上的控制压力为例,控制压力对每个小膜片造成的形变相同,对相邻的两个小膜片产生的形变方向相反,在膜盒端头产生的位移相互抵消,控制压力仅在控制腔顶端产生的形变转化成膜盒的位移。同理,中间压力仅在中间腔顶部产生的形变转换成膜盒的位移,环境压力仅在膜盒顶面产生的形变转换成膜盒的位移y。可得膜盒一般特性表达式如式(1)所示。

将膜盒面积代入式(1),可得膜盒压比位移方程如式(2)所示。膜盒的环境压力作用面积要大于控制压力的作用面积,使得膜盒在p0=p2时处于压缩状态,而膜盒的零位压比是膜盒处于自由伸展状态下控制压力与环境压力的比值,零位压比与膜盒的材料、结构有关,可作为膜盒性能的一个参量。通过理论分析,膜盒的零位压比为5.58。

p0(xSum-St)+p1Sm=ky

(1)

式中,x—— 控制压力与环境压力的压力比

Sum—— 内腔顶部受压面积,mm2

St—— 膜盒上部受压面积,mm2

Sm—— 中间腔顶部受压面积,mm2

k—— 膜盒整体的等效刚度,N/mm

y—— 膜盒位移,即压缩量,mm

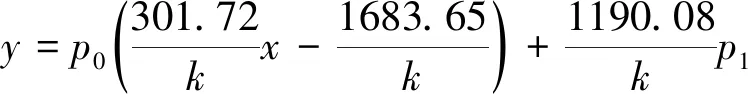
(2)

1.3 大小膜片间非真空对膜盒位移的影响

标准膜盒中,通常中间压力p1为0 MPa,但膜盒会出现“漏气”现象,使得中间压力p1不等于0 MPa,通过式(2)可得,此时p1将增加膜盒的伸出量。通过理想气体的状态方程可得,空气体积会影响膜片间压力变化,膜盒中间腔的高度为24 mm,正常工作位移为1.3～1.8 mm,则膜盒在正常工作过程中,由常态伸长到最大位置1.8 mm后中间压力p1变为0.93倍,前后变化误差为7%。因此认为膜盒在位移过程中,中间压力几乎没有变化,可认为是定值。因此,中间压力并不会对膜盒的位移产生很大的影响。

2 膜盒的有限元分析

2.1 有限元分析模型

建立精准的物理模型是得到符合实际有限元分析结果的基础。通过膜盒工作原理、结构特性分析可知,膜片为主要形变部分,为减少结构分析中的计算机运算量,省去限制膜盒初始压缩量的限位柱。

膜盒的工作原理与弹簧相似,可用广义胡克定律进行描述,广义胡克定律指出,固体的单向拉伸变形与所受的外力成正比且与材料的弹性模量和泊松比直接相关,膜盒的材料为AM350,密度为7800 kg/m3,弹性模量为1.9×105MPa,泊松比为0.3,抗拉强度为1267 MPa,屈服强度为1034 MPa,端头中心部分材料为橡胶,密度为1000 kg/m3。对于膜盒膜片产生的弹性变形,力与位移应满足式(3)。

K·δ=F

(3)

式中,K—— 系统结构刚度矩阵

δ—— 系统节点的位移矩阵

F—— 总的载荷矩阵

2.2 网格划分与求解

网格划分是有限元分析的重要过程之一,网格的质量会严重影响计算结果的精准度,因此对模型采用结构化网格划分。网格划分越密集,计算结果精度越高,但密集的网格会消耗大量的计算时间,延缓工作效率。金属膜盒的主要形变位置是大小膜片组,图4所示为单个膜片网格划分的半剖视图,主要网格限定参数有环向网格数MR、网格层数ML和中间段网格数MM。

图4 单膜片网格Fig.4 Single diaphragm grid

网格总体大小设定为5 mm,对不同环向网格数MR、网格层数ML和中间段网格数MM的网格进行计算,其结果如表1所示。总变形的最大误差值为1.27%, 认为网格对计算结果的影响可以忽略。如图5所示为计算所用的网格,大小为5 mm,网格数量为451878个,节点为2410892个。

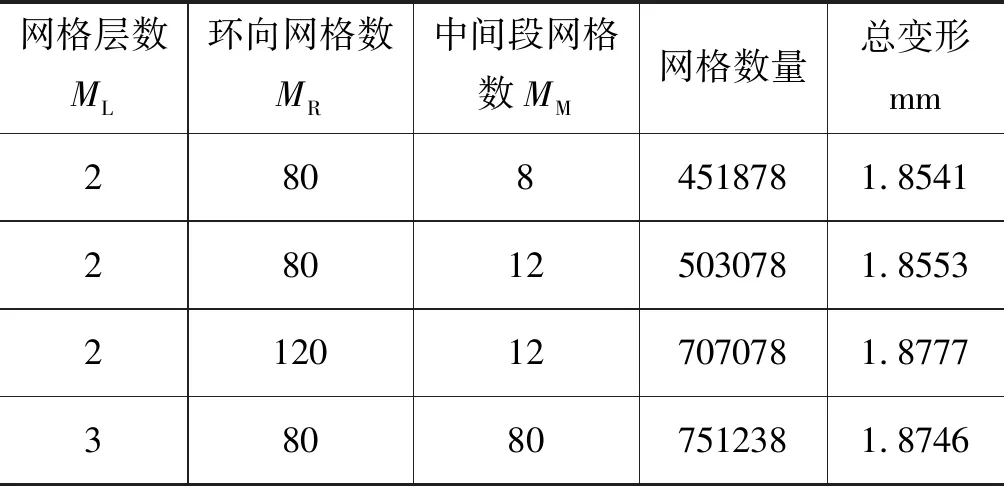
表1 不同网格参数下的总变形Tab.1 Total deformation under different mesh parameters

图5 膜盒网格划分结果Fig.5 Mesh division result of diaphragm bellow

根据使用工况,底面为固定约束,膜盒外侧与空气接触部分为环境压力作用面,膜盒内部与控制气体接触部分为控制压力作用面。设置环境压力分别为0.1013, 0.0899, 0.0799, 0.06305 MPa,以压比x为1,2,3,4,5的控制压力进行有限元仿真。如图6所示为膜盒的整体变形结果,由于底座的结构和固定约束,底座的整体变形量很小,膜片的变形从近底座侧向上呈现增大的趋势,膜盒端头部分的变形量在所有膜片的作用下最大,是表征膜盒性能的主要部位。

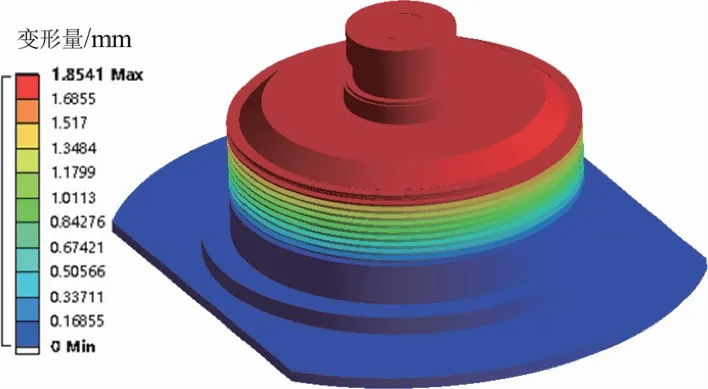
图6 环境压力及控制压力均为0.1013 MPa时膜盒变形量Fig.6 Deformation of diaphragm bellow when both ambient pressure and control pressure are 0.1013 MPa

金属膜盒的主要形变结构为大、小膜片,各级膜片形变叠加形成膜盒总位移。变形过程中产生的应力应变对膜片的疲劳特性和寿命具有重要的影响。如图7和图8所示为大、小膜片的应力云图和应变云图。应力和应变呈环状进行分布,其中膜片与膜片间贴合位置的应力和应变较小,中间层的应力应变较大,且呈现中间小两侧大的分布规律。应力应变最大位置在小膜片中间层内侧环形带,受到最大应力417.95 MPa,最大应变0.0022437,且在拐角处的结构内部出现应力应变较大值点。因此,膜片的中间层和内侧拐点是膜片结构优化的重要位置。

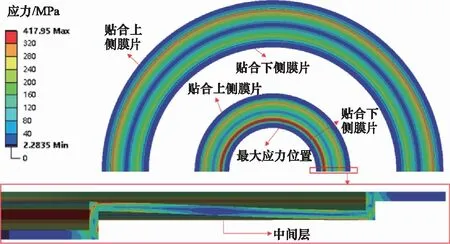
图7 大/小膜片应力云图Fig.7 Large/small diaphragm stress cloud

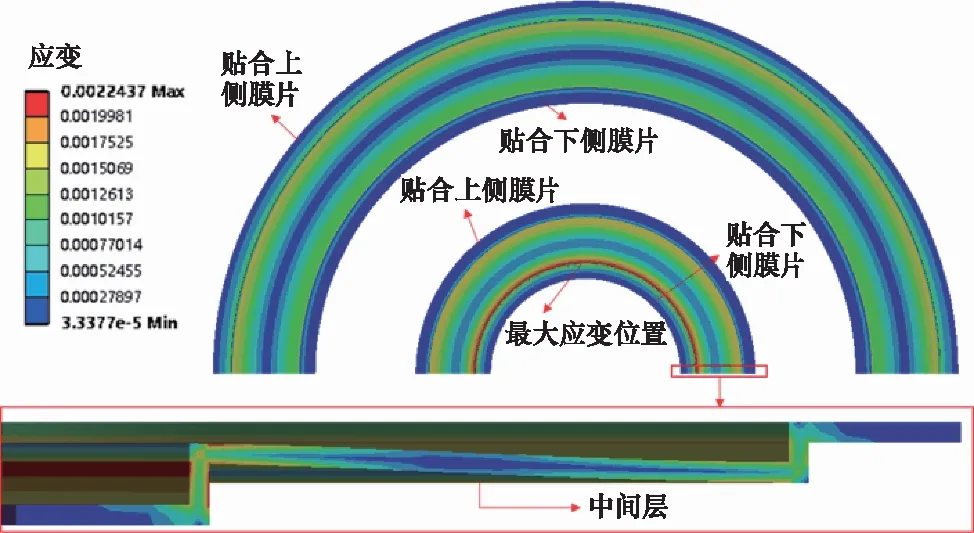
图8 大/小膜片应变云图Fig.8 Large/small diaphragm strain cloud

设膜盒的最大变形量即为膜盒的位移,图9为膜盒位移y随压比x的变化曲线,从图中可以看到,膜盒的位移随着压比的提升呈线性增加的趋势,且随着环境压力的升高,膜盒在同一压比下的位移不断减小。

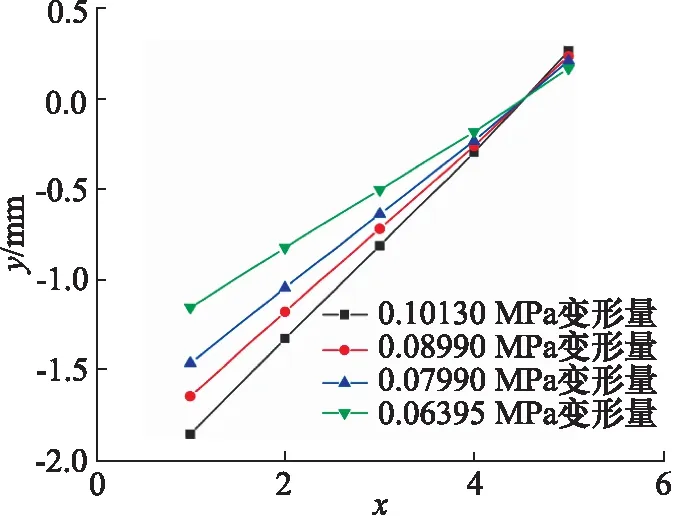
图9 不同环境压力下膜盒位移随压比的变化曲线Fig.9 Displacement curve of diaphragm bellow with pressure ratio under different ambient pressure

利用一元线性回归分析法对仿真结果进行归纳,预测x与y的回归方程如式(4)所示。拟合得到不同环境压力下,皮尔逊相关系数r大于0.99的仿真回归方程参数a、b,如表2所示。假定膜盒符合广义胡克定律,在压比为常量时,膜盒的位移变化量随环境压力的变化呈强线性关系,即参数a、b与环境压力p0呈线性关系,可得膜盒的一般规律方程,如式(5)所示。通过仿真得到膜盒的零位压比为4.536,这是因为仿真模型中存在初始压缩量,因此与理论计算值存在一定的差距。通过式(5)与式(2)可得膜盒等效刚度分别为58.13 N/mm和71.538 N/mm,取中间值64.834 N/mm作为膜盒的弹簧刚度。

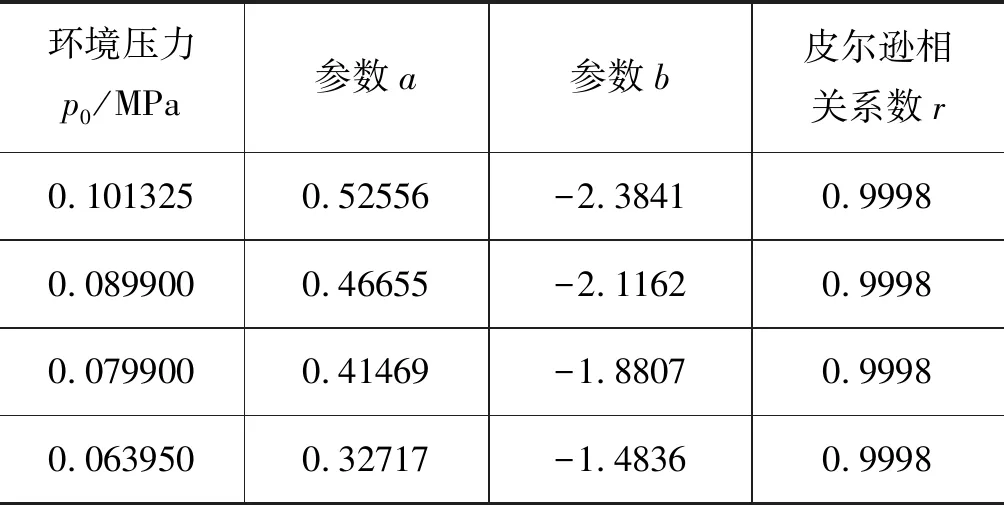
表2 仿真回归方程参数Tab.2 Simulation of regression equation parameters

yt=axt+b

(4)

式中,yt—— 第t个因变量的值,实际位移量

xt—— 第t个自变量的值,各个压比

a,b—— 回归方程参数

y=5.19p0·x-23.535p0

(5)

2.3 理论与仿真模型的修正

在有限元分析中,假设膜盒端头平面受到压力均为环境压力p0,但实际膜盒工作过程中随着位移量的增加,端头中间有直径为0.4 mm的圆形橡胶区域受到压力由p0逐渐升高到控制压力p2,这将产生一个变化的力f,使膜盒实际位移有所减小。此外,在膜盒伸出与缩回的过程中,端头的移动轨迹并不是沿着膜盒轴心进行,而是有少量的偏移。使得端头在运动过程中受到一个与运动方向相反的摩擦力Ff,因此,考虑力f与摩擦力Ff在膜盒上的力,可得膜盒的位移表达式如式(6)所示,膜盒的位移限制在1.5 mm以内。

(6)

由于有限元分析条件的限制,力f的大小需通过试验获得。摩擦力Ff在1～3 N以内。

3 膜盒压力-位移特性试验

3.1 试验模型

膜盒试验台如图10所示,控制气体通过入气口输入膜盒的控制腔,入气口和膜盒通过膜盒支架平稳固定安装在测试台上,支座用于模拟试验过程中膜盒端头侧面受到的摩擦力,支座与支架之间可拆卸,支架中间的通孔不影响位移传感器的测试,采用位移传感器支架将量程为0～5 mm的位移传感器固定,输出0～10 V的压力信号以反应位移变化量。

1.入气口 2.膜盒支架 3.螺栓 4.支座 5.支座支架 6.位移传感器支架A 7.位移传感器支架B 8.底板 9.位移传感器 10.金属膜盒图10 膜盒测试台Fig.10 Bellows test stand

在试验过程中,将膜盒放置在真空箱中以模拟环境压力,通过电气台控制环境压力与控制压力,由示波器接受位移传感器发出的信号。在标定传感器、连接气路并对膜盒进行密封性测试后,进行膜盒压力位移性能试验,得到膜盒的压力位移性能。

3.2 试验结果分析

为验证膜盒仿真结果,通过试验台测试得到不同环境压力下膜盒出程和回程工况下的膜盒位移y随压比x的变化曲线如图11所示。由于摩擦力等原因金属膜盒出程和回程之间存在滞环现象。通过拟合得到膜盒在不同环境压力下随压比的变化方程,皮尔逊相关系数高于0.96,结果高度相关,出程压力-位移表达式如式(7)所示,回程压力-位移表达式如式(8)所示。

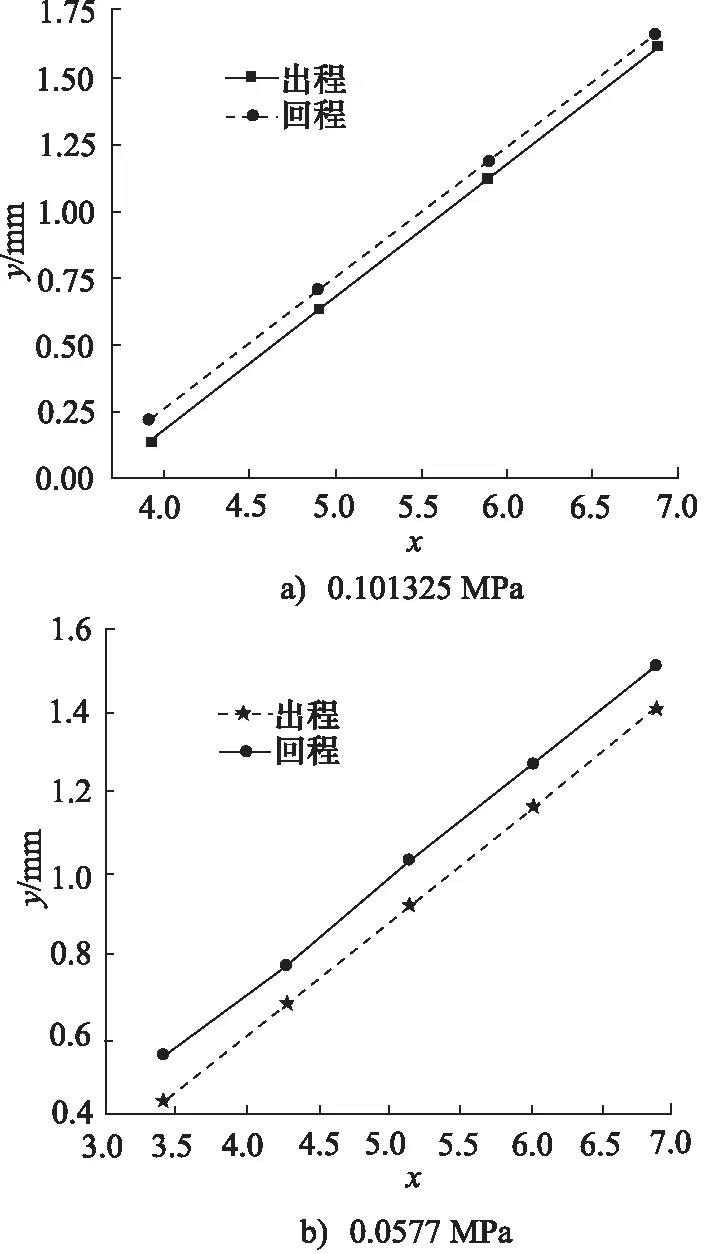
图11 不同环境压力下膜盒压比位移测试曲线Fig.11 Displacement test curve of membrane box pressure ratio under different ambient pressure

此时,膜盒出程的零位压比为5.935,回程的零位压比为6.114,与仿真结果的5.59误差分别是6.2%和9.37%。通过试验参数带入式(2)中可得膜盒的等效刚度的平均值为59.74 N/mm,与仿真得到的等效刚度误差为7.9%,进一步验证了仿真结果的准确性。试验得到的膜盒压比位移方程最后的常数项膜盒压比位移方程中的常数项由膜盒零位状态参考点、结合力f和摩擦力Ff造成。

y=4.92p0·x-29.2p0+1.15

(7)

y=4.81p0·x-29.41p0+1.3

(8)

4 膜盒参数对放气活门的影响

金属膜盒在放气活门中用作压力敏感元件,膜盒的压力-位移特性直接影响放气活门的控制性能。ZHANG JIN等[6]搭建了放气活门的整体模型,该模型采用出程和回程的压力-位移特性公式以表征金属膜盒特性,如图12所示。

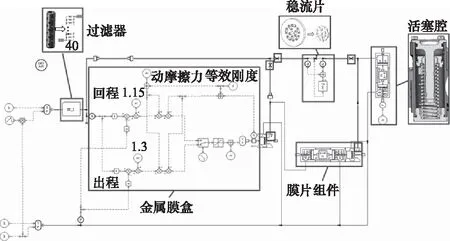
图12 放气活门整体模型Fig.12 Overall model of vent valve

等效刚度是膜盒的主要参数,根据式(2)、式(7)和式(8)可得膜盒不同等效刚度下的特性方程,代入放气活门整体模型探究不同膜盒刚度下放气活门使用特性。放气活门的控制压比起始为1,在时间t在0～4 s线性递增至最高值7.5,在4～8 s线性递减至1。

如图13所示为放气活门在不同膜盒刚度下活塞位移h随时间t的变化曲线,可得随着膜盒刚度的增高,放气活门在启闭时所需的压比提升,过高的膜盒刚度会造成放气活门在工作压力下较难打开或打不开的现象。

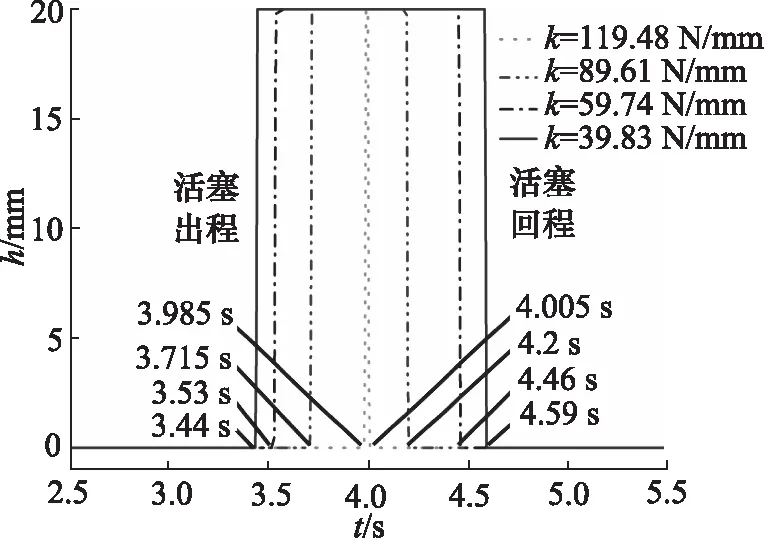
图13 不同膜盒刚度下的活塞位移曲线Fig.13 Piston displacement curve under different membrane box stiffness

5 结论

本研究对某型金属膜盒的工作原理进行分析并推导出膜盒压比位移的一般性方程,建立膜盒的有限元模型,通过有限元分析和试验两方面对膜盒的压力位移特性进行分析,得出以下结论:

(1) 通过理论推导得到膜盒组件压力-位移的一般性表达式,并且中间压力不会对膜盒的位移产生很大的影响;

(2) 在工作过程中,膜片的应力应变呈环带装分布,小膜片的中间层内侧出现应力应变最大值,是结构优化的重点位置;

(3) 通过有限元分析得到了膜盒的压力-位移表达式,膜盒的位移有随着压比的提升呈强线性增加的趋势,且随着环境压力的增加,膜盒在同一压比下的位移不断减小;

(4) 搭建膜盒压力-位移特性试验台,验证了仿真中得到的膜盒压力位移特性的准确性;

(5) 随着膜盒刚度的提升,放气活门启闭过程所需的压比升高。