小型双脉冲发动机金属膜片的承压与破裂*

徐 明，封 锋，曹钦柳，党建涛

（1. 南京理工大学机械工程学院，江苏 南京 210094；2. 中国航天科技七院，四川 成都 610100）

双脉冲固体火箭发动机是一种多脉冲固体火箭发动机，因其结构简单、稳定性高等优点，被广泛应用[1-3]。隔离装置是双脉冲固体火箭发动机的一项关键技术，其主要作用是防止一脉冲燃烧室内的高温高压燃气侵入到二脉冲燃烧室内，以保证双脉冲发动机两个燃烧室的独立性。隔舱式[4]脉冲固体火箭发动机采用硬质材料作为隔离装置，具有结构简单、适用性强等优点。隔舱式双脉冲发动机的隔离装置根据材料的不同又可分为喷射棒式、陶瓷隔板和金属膜片。喷射棒式[5]隔板承压能力强、加工简单、可靠性高，但结构质量和体积较大，增加了发动机消极质量。陶瓷式[6]结构质量较大且承压与破裂压强比较小，同时对材料要求较高，导致该类型隔离装置在脉冲发动机的应用受到较大限制。

金属膜片隔离装置由支撑架、盖板、带有预制刻痕的金属膜片构成。支撑架用来支撑金属膜片，其轮辐与金属膜片上的预制刻痕对齐。金属膜片具有预制刻痕的一侧置于一脉冲燃烧室，在轮辐的支撑下保证金属膜片能承受住一脉冲发动机工作时的压力冲击。在二脉冲点火压力冲击下，金属膜片可按照预制刻痕破裂。1994 年，德国BC/P 公司提出了金属膜片隔离技术并应用于双脉冲固体火箭发动机实验，2001～2003 年，该公司研发出更轻质的金属膜片隔离装置并应用于120 mm 口径的双脉冲固体火箭发动机[7]。Naumann 等[8]研制了一种铝质膜片双脉冲发动机，并取得点火试验成功。王伟等[9]建立了金属膜片的破裂压强与结构尺寸之间的定量关系，同时做了大量相关的热流实验，验证了所设计的金属膜片结构满足双脉冲固体火箭发动机的使用要求。

本文中，建立金属膜片的三维有限元模型，利用仿真软件对金属膜片的承压及破裂过程进行数值模拟，分析金属膜片在承受一脉冲点火压力下的完整性，利用Johnson-Cook 损伤模型[10]模拟金属膜片的破裂过程。设计一套双向测压装置，验证金属膜片承压和破裂符合设计要求。利用数值模拟，分析在相同厚径比时不同尺寸的金属膜片破裂时所需压强的规律。

1 数值计算

1.1 金属膜片结构

金属膜片需要在一脉冲工作时保持结构的完整和密封，在二脉冲工作时按预制刻痕破裂且产生的碎片不脱离，达到保证发动机正常工作的目的。

实验中采用黑火药产生高温燃气建压，可以较好地模拟发动机的工作情况。为防止金属膜片的力学性能受高温产生较大影响，在金属膜片上涂防热层来达到隔热效果。

在高温高压下，为保证在二脉冲工作时金属膜片的破裂压强较小，在金属膜片上刻有十字型或米字型预制凹槽[11]，凹槽截面为三角形。采用金属膜片结构为十字槽外加四个圆弧槽。金属膜片如图1所示。

金属膜片材质为2A12 铝合金[12]，是航天领域大量使用的铝合金材料，其力学性能较好，机加工艺较简单。三维结构如图2 所示。

图 1 金属膜片Fig. 1 Metal diaphragm

图 2 金属膜片的三维结构Fig. 2 Three-dimensional structure of metal diaphragm

根据文献[13]，带有刻痕金属面的力学性能会减弱。在装配时需将带有刻痕的一面对准一脉冲的燃烧室，并且让十字刻痕要对准支撑架的轮辐，以提高一脉冲工作时金属膜片的承受能力，保证发动机正常工作。

1.2 模型的建立

采用ABAQUS/explicit 软件对金属膜片的承压过程、破裂过程进行数值模拟。燃烧室内高温高压燃气对金属膜片的冲击作用可以近似为，一个瞬间恒定压力作用在一个有限平面上，并且受力均匀。载荷设定为恒定压力。模型的网格单元网格类型为C3D4。支撑架的网格尺寸设置为0.3 mm。金属膜片的网格尺寸为0.2 mm（在预制刻痕处的网格尺寸为0.1 mm）。依据经验选择网格尺寸。模型网格的尺寸越小，则网格数量相对越多,数值计算精度相对更准确。根据文献[14],模型的网格数量对数值计算精度和计算时间会有很大的影响。通常，随着模型网格数量的增加，数值计算结果会更加准确，但计算时间也会变长。所以，确定网格数量应在计算精度、计算时间两个方面上权衡。在数据梯度变化较大的位置(如应力集中处)，为了精确反映数据变化规律，需对此位置划分比较密集的网格。在十字预制刻痕处为应力集中，需要进行网格加密处理，此处网格尺寸设定较小。而在数据梯度变化较小的位置，则相应划分相对稀疏的网格。这样，整个模型的网格结构呈现出疏密不同的分布，更有利于得到准确的计算结果。

在金属膜片承压模拟过程中的载荷设置：在受到一脉冲点火压强作用面上布置50 MPa 的压强，方向垂直于金属膜片。设定一脉冲工作时间为10 ms，符合设计的双脉冲固体火箭发动机一脉冲工作时间。在金属膜片破裂模拟过程中的载荷设置：在受到二脉冲点火压强作用面上布置5 MPa 的压强，方向垂直于金属膜片。设定二脉冲工作时间为10 ms，符合设计的双脉冲固体火箭发动机二脉冲工作时间。

金属膜片的承压计算模型如图3 所示，金属膜片破裂计算模型如图4 所示。

图 3 金属膜片的承压计算模型Fig. 3 Pressure calculation model of metal diaphragm

图 4 金属膜片的破裂计算模型Fig. 4 Rupture calculation model of metal diaphragm

采用Johnson-Cook 损伤模型，该模型能够较好地描述板材结构的损伤情况。从损伤演化角度，ABAQUS 中的损伤演化是从损伤萌生开始计算的。在ABAQUS 中，利用Johnson-Cook 损伤模型进行材料失效模拟时，ABAQUS 会自动默认最初的损伤因子为0，在材料处于断裂状态下损伤因子为1。金属膜片破裂过程与ABAQUS 中损伤演化过程非常接近，因此使用Johnson-Cook 损伤模型模拟金属膜片破裂的过程。损伤演化采用位移求损伤变量方法，原因是在二脉冲点火压强作用下金属膜片应力集中处最先产生裂纹（位移的相对变化）。2A12 铝合金不同应变率下应力应变关系参见文献[15]。

Johnson-Cook 失效模型包含了应力三轴度、应变率以及温度对失效应变的影响，适合于描述金属在高温高应变率下的破坏现象。基于Johnson-Cook 损伤模型描述2A12 铝合金的失效行为，Johnson-Cook 模型中的失效累积并不直接使屈服面退化，定义失效时的应变为[15]：

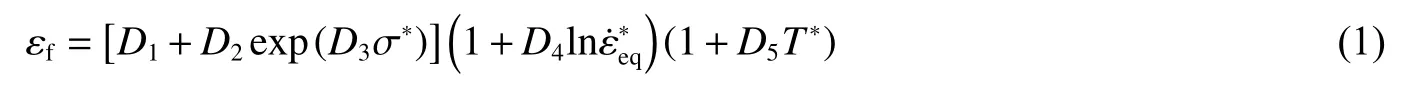
式(1)中的三个部分依次表示断裂应变随着静水应力张量的增加而减小、增加的应变率对失效应变的影响效应、材料延性的热软化效应。

损伤参数为：

式中：Δεeq为一个积分循环的等效塑性应变增量，εf为当前时间步下的有效断裂应变。损伤参数D 为一个积累量，当损伤参数D 达到1 时，有限元模型将会发生破裂，模型中的网格单元将会被自动删除。

金属膜片和支撑架的参数见表1[15-19]，2A12 铝合金的材料参数分别为[15]：材料在参考应变率和参考温度下的初始屈服应力A=400 MPa，硬化常数B=424 MPa，应变强化指数n=0.35，温度软化系数m=1.426，应变率敏感系数C=0.001，Tr=293 K，Tm=863 K，D1=0.116，D2=0.211，D3=2.172，D4=0.012，D5=−0.012 5，=0.001 s−1。

表 1 金属膜片和支撑架的参数Table 1 Parameters of metal diaphragm and support frame

1.3 计算结果分析

根据双脉冲发动机的设计要求，本文中设计了四种规格的金属膜片，见表2。采用上述Johnson-Cook 损伤模型，对金属膜片承压过程、破裂过程进行数值模拟，得到四种规格金属膜片的数值模拟结果，见表3，发现金属膜片D 的承压与破裂效果符合要求。

表 2 金属膜片尺寸Table 2 Metal diaphragm size

表 3 金属膜片结构的完整性Table 3 Structural integrity of the metal diaphragm

1.3.1 承压过程

当金属膜片和支撑架承受一脉冲工作压强作用时，金属膜片和支撑架同时向二脉冲方向发生轴向形变。根据设计要求，一脉冲工作压强为50 MPa。金属膜片因带有预制刻痕，其承载能力降低。因此，用支撑架和金属膜片共同承受一脉冲工作压强，使金属膜片薄弱部位形变量减小。承压模拟分析主要考察，金属膜片在一脉冲工作压强冲击下结构完整性是否遭到破坏。数值模拟计算的金属膜片应变分布图，如图5 所示。金属膜片预制刻痕处的应变明显比其他部位的应变小，表明支撑架和金属膜片共同承受了来自一脉冲的压强。金属膜片的应力分布，如图6 所示。在承压状态下，金属膜片所受的应力与其抗拉强度相比，稍微有点误差。

图 5 承压状态下金属膜片的应变Fig. 5 Strain of metal diaphragm under pressure

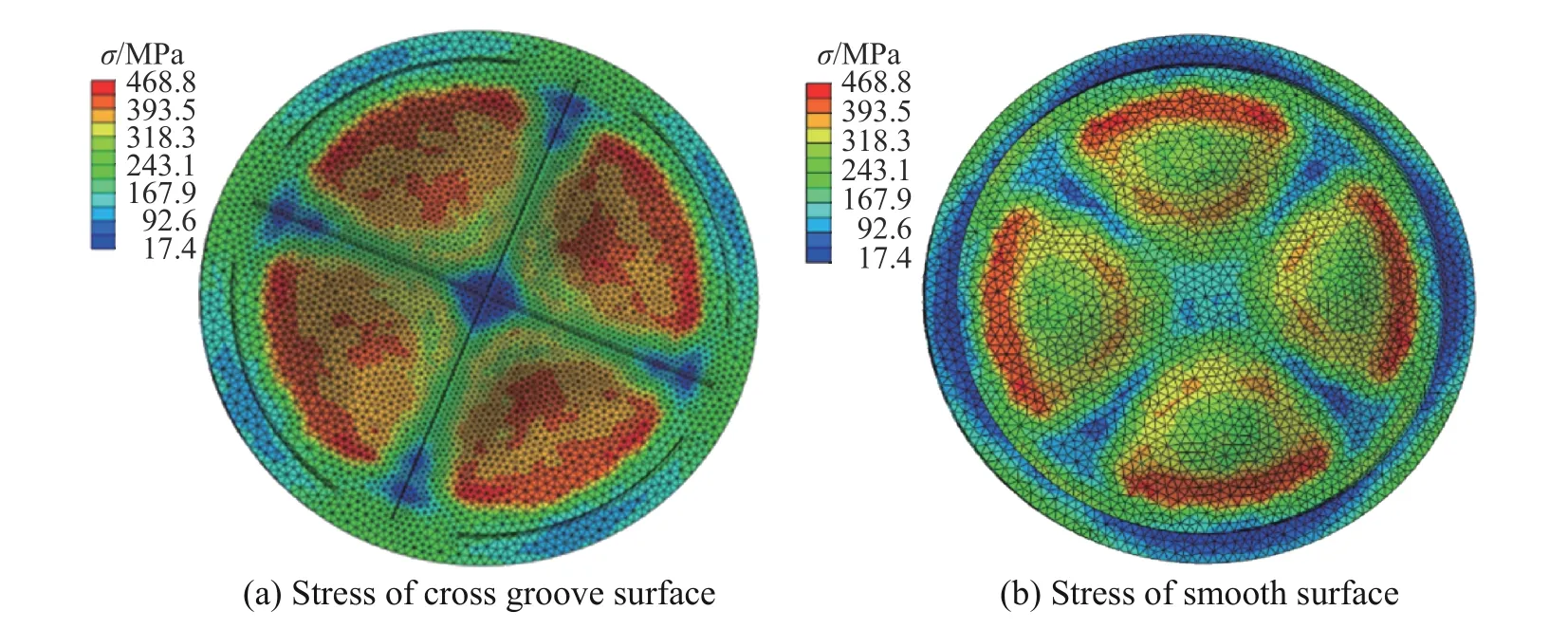
图 6 承压状态下金属膜片的应力Fig. 6 Stress of metal diaphragm under pressure

最大应变出现在与支撑架轮辐接触的边缘的位置，其应变数0.074 21 没有达到断裂应变εf=0.08[18]，所以金属膜片的结构完整性保持完整。通过数值计算的支撑架应变分布，如图7 所示。在支撑架上，产生较大应变的位置是轮辐的根部和轮辐的中心位置，与实际情况相符合。支撑架的最大应变0.021，没有超过其断裂应变εf=0.057[19]，不会发生断裂损伤。这样，发动机一脉冲正常工作。数值计算支撑架的应变分布，如图8 所示。在承压状态下，支撑架所受的应力只有很少一部分超过支撑架的抗拉极限，但不影响支撑架的正常使用。

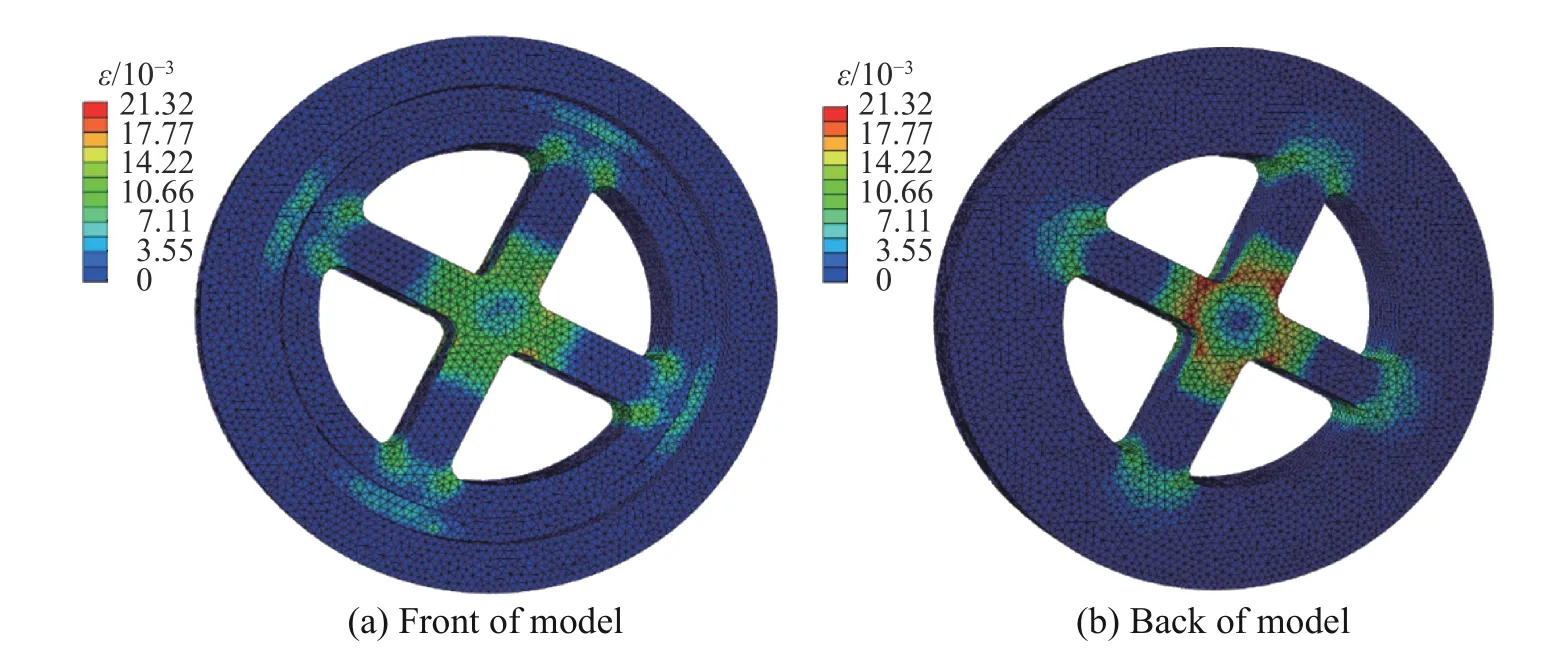
图 7 承压状态下支撑架的应变Fig. 7 Strain of support frame under pressure

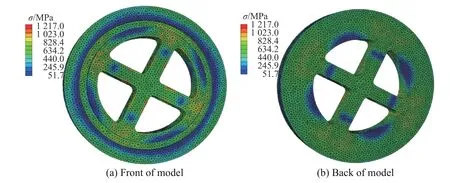
图 8 承压状态下支撑架的应力Fig. 8 Stress of support frame under pressure

1.3.2 破裂过程

利用Johnson-Cook 损伤模型，模拟金属膜片预制刻痕的断裂过程。在二脉冲工况下，随着燃烧内的压强迅速增加，金属膜片开始发生形变，其预制刻痕处的应变逐渐增加。当金属膜片中心位置预制刻痕处的应变达到断裂应变εf=0.08[18]时，预制刻痕位置开始出现裂纹。随着燃烧室压力增加，预制缺陷处的裂纹迅速扩展，直到整个金属膜片在中心位置处出现贯穿型的裂纹，致使整个膜片失去承载能力。金属膜片破坏过程的应变分布如图9～11 所示。

图 9 0.021 ms 时刚出现裂纹Fig. 9 Crack just appeared at 0.021 ms

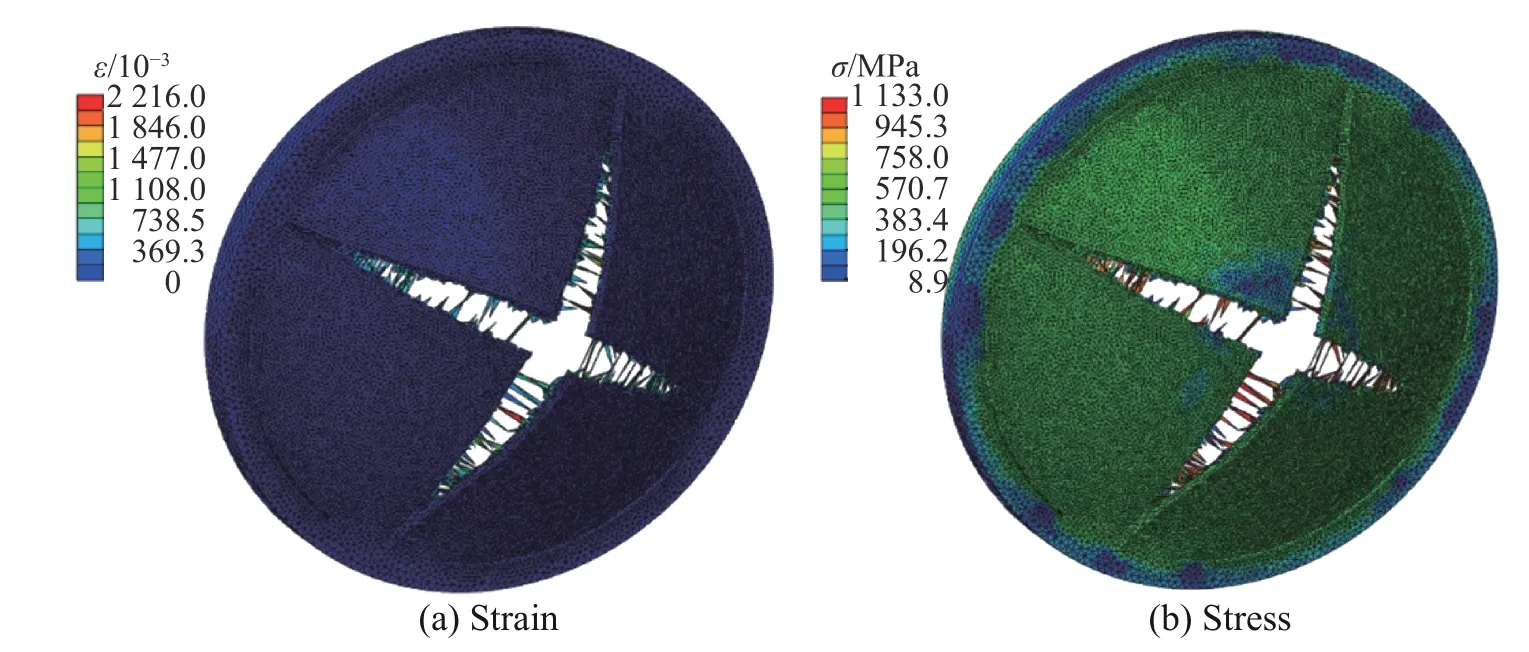
图 10 0.027 ms 时中间破裂状态Fig. 10 Intermediate rupture state at 0.027 ms

图 11 0.038 5 ms 破裂结束状态Fig. 11 Rupture end state 0.038 5 ms

在0.038 5 ms 时，金属膜片达到了最终的破裂状态。考察金属膜片内侧根部，由于部分单元的应变已经超出材料的断裂应变，相应单元已经由ABAQUS 自动删除。由于金属膜片根部的单元并未在整个厚度方向都失效，大部分材料单元表面只发生损伤，因此金属膜片在根部并不会发生断裂。这也说明，本文所设计的金属膜片不会有块状碎片飞出。

2 实验验证

2.1 实验布设

实验布设示意图如图12 所示，测压室内黑火药通过计算机控制点火，发动机测控仪接收压力传感器信号，计算机将压力数据图像化处理，清晰地呈现压强变化趋势。

2.2 实验装置

测压装置由前堵盖、支撑架、金属膜片、测压室、固定盖、后堵盖等部件构成。测压装置结构示意图如图13 所示。测压装置(金属膜片除外)采用30CrMnSiA(合金结构钢)[17]，能承受高温燃气烧蚀，保证测压装置重复使用。

测压装置优点：测压室内建立一脉冲、二脉冲点火压强；支撑架正向、反向连接测压室，分别实现一脉冲金属膜片承压、二脉冲金属膜片破裂；螺纹连接密闭性良好。

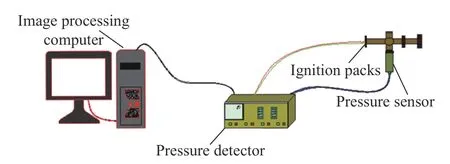
图 12 实验布设Fig. 12 Experimental device

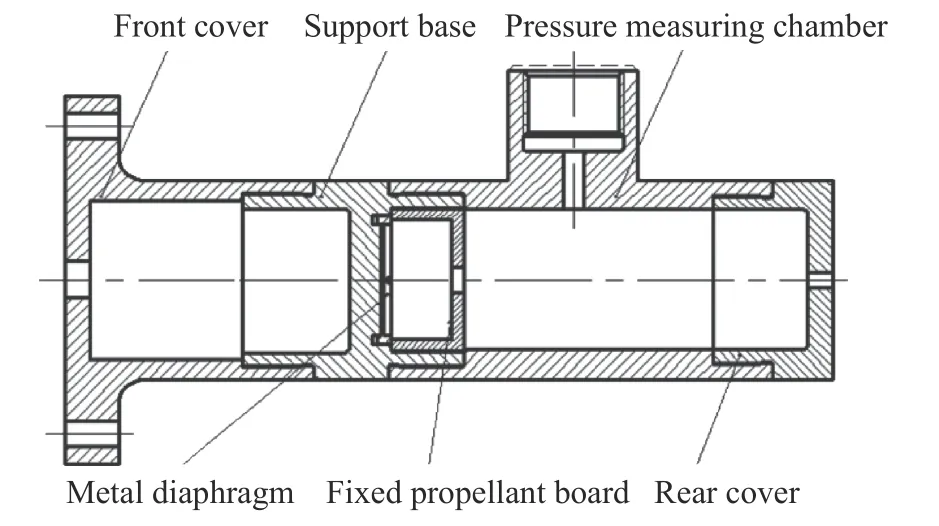
图 13 测压装置结构Fig. 13 Pressure measuring device

2.3 实验结果

对金属膜片D 的实验结果进行详细分析。通过压力传感器记录燃烧室内压强的变化情况。对金属膜片D 分别进行5 次的承压实验、5 次的破裂实验。一脉冲工作时，金属膜片承压时压强曲线如图14 所示。

承压压强曲线一致性较好，金属膜片的承受压强分别为50、51、55、45、46 MPa。二脉冲工作时，金属膜片破裂的压强曲线如图15 所示。破裂压强曲线一致性较好，金属膜片破裂压强分别为6.1、5.3、6.3、5.0、5.2 MPa。

一脉冲工作时，金属膜片D 的承压实验结果如图16 所示，在预制刻痕处发生轻微的少量变形。刻痕的背面处有支撑架支撑，所以在一脉冲工作时，金属膜片D 能承受50 MPa 压强的冲击。

图 14 承压实验的压强Fig. 14 Pressure curves of pressure tests

图 15 破裂实验的压强Fig. 15 Pressure curves of crack tests

图 16 承压实验后的金属膜片DFig. 16 Metal diaphragm D after pressure test

图 17 破裂实验后的金属膜片DFig. 17 Metal diaphragm D after crack test

二脉冲工作时，金属膜片D 的破裂实验结果如图17 所示，金属膜片D 破裂的程度符合预期效果。金属膜片上因带有预制刻痕，应力集中必然存在。金属膜片D 按照预制刻痕打开成四个小花瓣形状，有利于高温燃气顺利排出，防止发动机燃烧室压力过大，给发动机正常工作提供了一定的保证。

金属膜片D 的实验结果与数值模拟计算结果基本相符，基本验证了金属膜片D 满足双脉冲发动机的设计要求。同时，也表明本文的数值模拟方法具有一定的可行性。

采用数值模拟的不足之处是没有考虑金属膜片所处的高温环境因素，在数值模拟计算结果上会有一些误差。高温环境促进金属膜片的变形，通过实验获得金属膜片的变形结果在一定程度上大于数值模拟的变形结果。实验验证得到的结果满足设计要求，说明数值模拟在没有考虑温度因素而获得的结果也是满足设计要求的，因此温度因素对数值模拟结果影响较小。

3 金属膜片破裂规律

由上所述数值模拟和实验可知，金属膜片D 符合设计要求。金属膜片D 的厚径比0.7 mm/28 mm=0.025，十字刻痕处有效厚度比0.2 mm/0.7 mm=0.286，四个圆弧处的有效厚度比0.4 mm/0.7 mm=0.571，其所在的位置距金属膜片中心的比例12.5 mm/14.0 mm=0.89。按照这样的比例，设计了一系列尺寸的金属膜片结构，如表4 所示。表中，也列出下面推算的出现裂纹时的压强。

利用本文中有效的数值模拟方法，探求随着双脉冲固体火箭发动机口径的增大金属膜片按照预制刻痕发生破裂时所需压强的规律，避免了通过实验摸索大尺寸金属膜片的破裂时所需的压强规律时的不方便。所以，探求不同尺寸的金属膜片的破裂时所需要压强的规律很有意义，能为设计大口径的双脉冲发动机的金属膜片提供参考依据。

表 4 金属膜片参数Table 4 Metal diaphragm parameters

利用Johnson-Cook 材料损伤模型对表4 中的金属膜片模型进行破裂数值模拟，得到不同尺寸的金属膜片在产生裂纹时的应变云图，如图18 所示。图18 中，Δt 为金属膜片在载荷的作用下应变达到断裂应变εf=0.08 时产生裂纹的时间。

图 18 不同尺寸的金属膜片D 在产生裂纹时的应变云图Fig. 18 Strain clouds of different metal diaphragm D when cracks occur

在Step 模块中Time period 设为0.001 s，在金属膜片模型上施加线性载荷，可根据金属膜片产生裂纹时的Step time 推算压强载荷，见表4。

根据表4 中的数据拟合得到金属膜片的直径、厚度和产生裂纹时压强的拟合关系，如图19 所示。厚径比为0.025 时，金属膜片产生裂纹时的压强的大致规律如下。

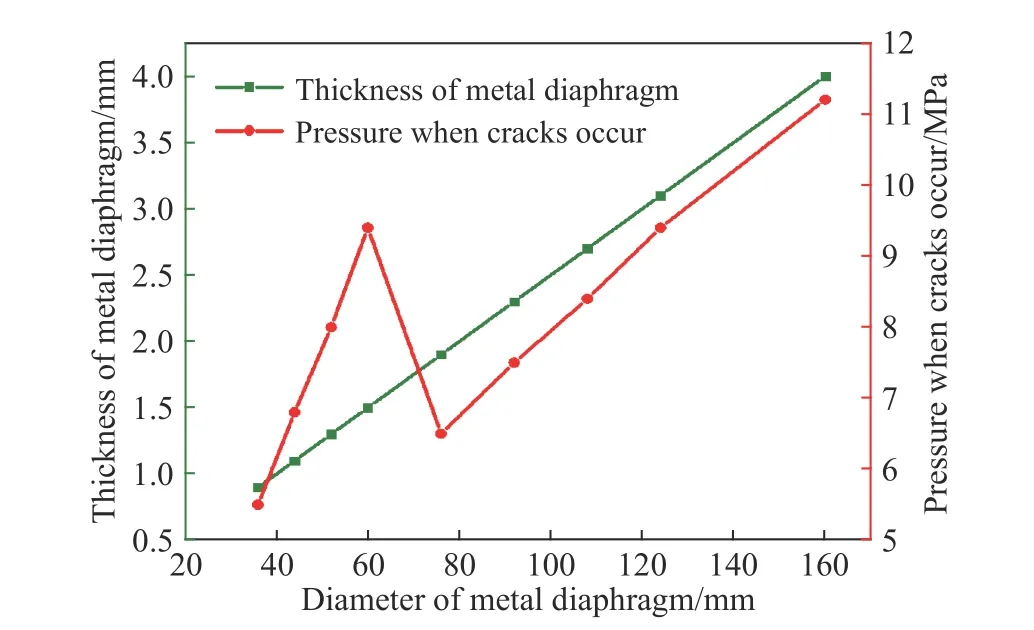
图 19 金属膜片D 的直径、厚度和产生裂纹时压强的拟合关系Fig. 19 Fitting relationships between diameter and thickness of metal diaphragm D and pressure when cracks occur

4 结 论

利用有限元数值模拟，计算得到金属膜片的承压、破裂时的应力应变分布情况。并且，利用损伤模型模拟金属膜片破裂的失效。能比较准确地模拟金属膜片破裂时的压强。通过对金属膜片进行了承压实验、破裂实验，验证了金属膜片结构的合理性。并得到以下结论。

（1）利用Johnson-Cook 损伤模型，对金属膜片的破裂过程进行仿真模拟，最先在应力集中处(金属膜片刻痕的中心位置)发生破裂，并且金属膜片的后续破裂会沿着预制刻痕的继续发展下去。

（2）金属膜片D 在一脉冲工作时，金属膜片能够承受50 MPa 点火压强的冲击作用。在二脉冲工作时，金属膜片破裂压强为5 MPa，金属膜片D 在实验和数值模拟中均得到了较好的验证，基本符合设计要求。

（3）利用本文有效的数值模拟方法，得到不同尺寸的金属膜片(厚径比等于0.025)按照预制刻痕产生裂纹时所需的压强，先增大后减小然后再增大。为了能更准确地给出不同尺寸金属膜片在产生裂纹时所需压强大小的规律，今后在数值模拟中应详细地考虑燃烧室温度这个因素。