气动柔性细长管道机器人的结构设计及特性分析

王伟进, 严鲁涛, 李海源

(北京邮电大学 现代邮政学院(自动化学院), 北京 100876)

引言

如今,机器人得到了很大的发展,不同种类的机器人已经应用到许多领域来替代人类工作[1-4],特别是管理和维护人们生活中最重要的生命线(水、污水、煤气等)的机器人,以及有关核管道[5]的维护与探测的机器人,由于维护成本高,劳动力资源有限,需求不断增加[6]。人口密集地区管道系统的维护至关重要,管道系统的故障会影响到人类的日常生活;偏僻荒芜地区,管道事故也会给工厂、城市带来巨大的损失[7]。

管道机器人作为一种有效的探测设备,可以深入人无法到达的狭小空间内执行勘查任务[8]。多年以来,人们研究了各种管道机器人运动机构的设计,用来实现水平运动、垂直运动、变径运动、 拐弯运动等设计目标[9]。

目前的管道机器人可以分为:PIG(Pipe Inspection Gauge,管道检具)式,轮式,螺旋式, 蠕动式,履带式,压壁式,这些技术可以单独使用也可以组合使用[10]。

文献[11]介绍了一种PIG式管道机器人,通过更换外表的密封模块,可以探测直径在50～150 mm之间的管道。文献[12]提出了一种轮式机器人,使用对称安装的3对轮,可以穿过150～200 mm的管道。文献[13]通过将行星齿轮传动直接作用在驱动轮,设计了新型的主动螺旋管道机器人,可以适应直径75～100 mm的管道。文献[14]通过模仿蚯蚓,设计了一种气动管路的管道机器人,可以在直径50 mm管道内运动,在弯道内具有较好的适应性。文献[15]设计了一种履带式机器人,使用弯曲轨道,安装永磁铁从而产生牵引力与附着力,并且使用直径为20 mm和30 mm的管道进行了实验。文献[16]介绍了一种压壁式管道机器人,通过改变自身的最大直径可以通过直径150～230 mm的管道。表1展示了各个类型机器人的特点。

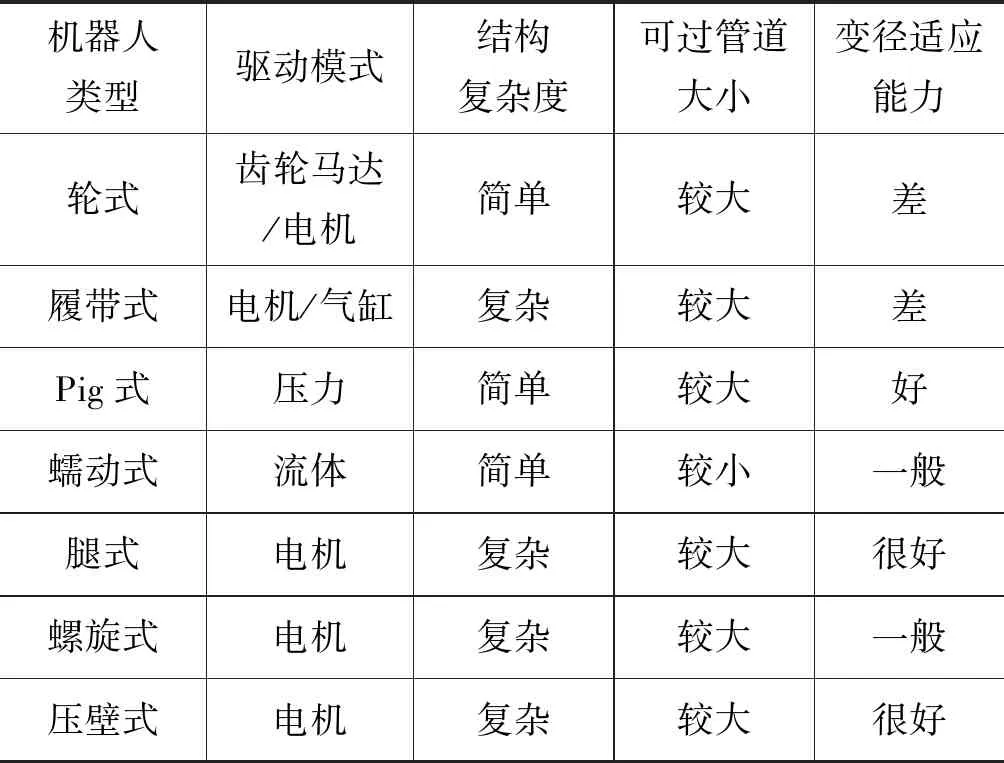
表1 机器人类型比较分析Tab.1 Comparative analysis of robot types

然而,管道的检查与探测是一项艰巨的任务,特别是当管道的内径和弯曲半径非常小时,人类无法到达。因此,研发一种适用于小管径、小拐弯半径的管道机器人是很有必要的。

本研究旨在设计一种适用于长细管道的机器人,阐述工作原理与系统设计,建立机器人的运动模型并分析特性,最后搭建实验系统,结合实验结果进行分析与讨论。

1 工作原理与系统设计

管道机器人由于其驱动元件尺寸的限制,导致适用的管道半径与拐弯半径过大,本研究提出一种气动驱动的柔性管道机器人(如图1a所示),将气泵外置,柔性气管与机器人相连,柔性气管可以跟随机器人适应管道,解決刚性管道机器人适应性差的缺点[17]。由一个气动针阀,两个橡胶锥形垫组成,其中锥形垫具有相对于运动方向相反的圆弧,分别固定在针阀的伸长部分和后部分,锥形垫的尺寸比适用的管道稍大,因此锥形垫有轻微的压缩量,形成摩擦力。

图1b展示了锥形垫在管道内的形变状态。位置a为前锥形垫伸长后形变变化,红色标识所示。当前锥形垫缩回到位置a′,由于锥形垫本身的构型导致锥形垫的压缩面积增大,导致摩擦力变大,定义此时的最大静摩擦力为fmax。

图2所示为机器人在管道内运动原理。阶段1为机器人的初始状态,此时,针阀保持原长不变。通气后,针阀前部分克服锥形垫的摩擦力向前伸出,后部分则由于没有动力保持原位置,形成阶段2。断气后,在阶段3,由于针阀的缩回力不足以克服前部分锥形垫的最大静摩擦力fmax,导致伸长部分不能回到原来的位置(阶段3的虚线部分),而反作用力克服后部分锥形垫带来的摩擦力,带着机器人后部分向前运动(阶段3的实线部分)。三个阶段构成一个完整的运动周期,X即为一次周期运动的位移。

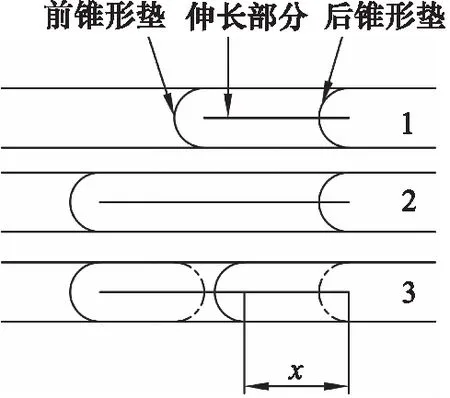
图2 运动原理Fig.2 Motion principle

机器人的各部分参数如表2所示。

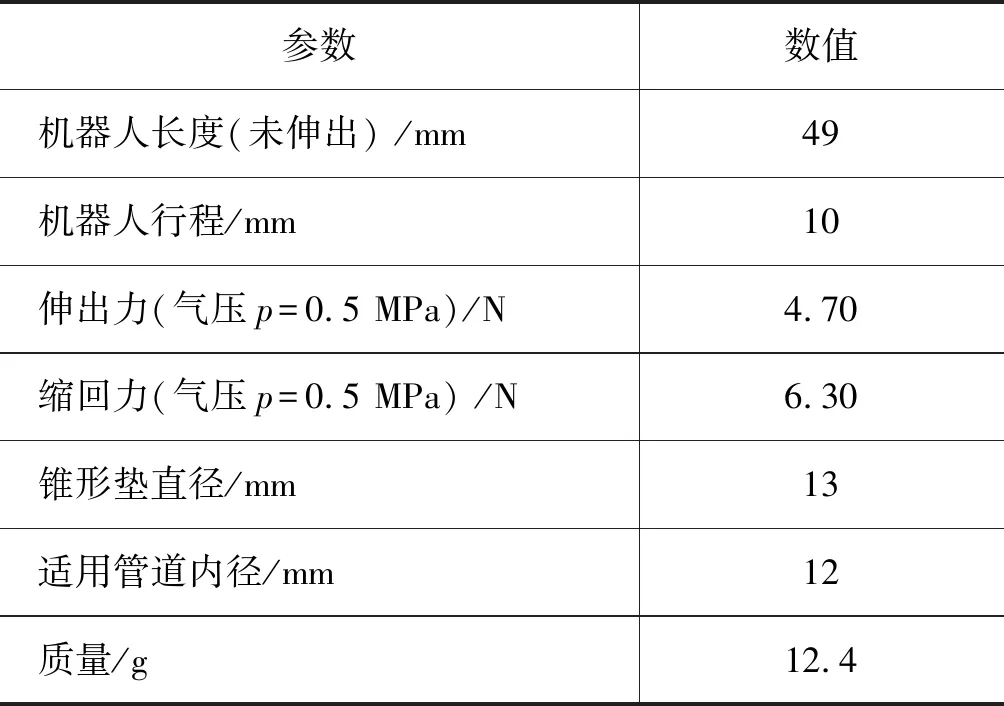
表2 机器人性能参数Tab.2 Robot performance parameter

2 机器人运动模型及特性分析

2. 1 运动分析

运动分析即管道机器人能否在给定的管道中前进,如图所示由以下三个部分组成。

1) 在直道中

如图3所示两个锥形垫初始位置分别为a1,b1,移动到直道的末端位置a2,b2。当前部分移动,后部分不动时,后部分受到最大静摩擦力fmax作用,前部分受到沿管道运动的滑动摩擦力。b、a代表前后锥形垫的位置。F1,f1,F2,f2分别代表前部分推力,前锥形垫摩擦力,前部分缩回力,后锥形垫摩擦力,下标数字代表不同的阶段。

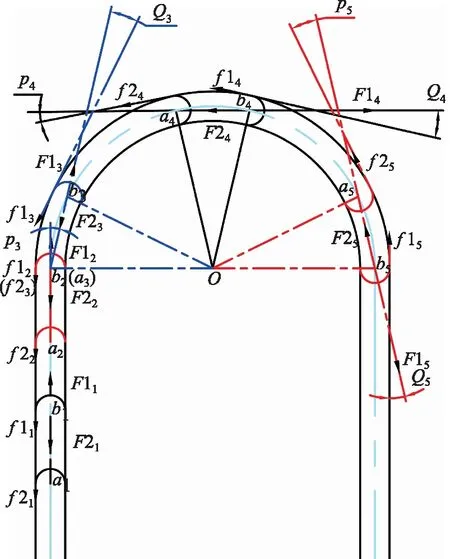
图3 运动过程Fig.3 Motion process

机器人从点a1运动到点a2,前部分向前推力F11变为F12,后部分缩回力F21变为F22,前部分摩擦力f11变为f12,后部分摩擦力由f21变为f22。

即当机器人整体处于直道中,位置的改变并不影响各个力的变化。所以在直道中运动的力学条件为:

(1)

式中,F11,f11—— 直道内前部分推力、摩擦力

F21,f21—— 直道内后部分缩回力、摩擦力

2) 在过渡处

当机器人一部分处于弯道内,一部分处于直道内,即后锥形垫从a2位置运动到a3位置,机器人处于过渡处。当机器人在过渡处,前柔性锥形垫会随着管道的形状变化,从而适应管道。

机器人从点a2,b2运动到点a3,b3,前部分的摩擦力由f12转化为f13,后部分的摩擦力由f22转化为f23,前部分的推力由F12转化为F13,后部分的缩回力由F22转化为F23。在运动过程中,线段oa2逐渐减小,最终减少到最小值oa3,而a2b2=a3b3,ob2=ob3。所以,机器人在过渡处运动过程中,∠Q逐渐增大,∠P逐渐增大。当机器人后部分的圆心位于拐弯半径的圆心交点a3处,∠Q达到最大值,∠P达到最大值。随着∠Q不断增大,前部分推力F1在摩擦力方向的分力不断减小,后部分缩回力F2逐渐减少,后锥形垫因为还在直道内,摩擦力维持不变。

此时,机器人运动的条件为:

(2)

式中,F13,f13—— 过渡处前部分推力、摩擦力

F23,f23—— 过渡处后部分缩回力、摩擦力

Q3—— 前部分推力与摩擦力最大夹角

p3—— 后部分缩回力与摩擦力最大夹角

3) 整体在弯道内

机器人从a3,b3运动到a4,b4再到a5,b5。前部分推力从F13变为F14,最后变为F15;前部分摩擦力由f13变为f14,最后变为f15;后部分缩回力从F23变为F24,再变为F25;后部分摩擦力由f23变为f24,最后变为f25。

当机器人整体在弯道内时,有oa3=ob3=oa4=ob4=oa5=ob5和a3b3=a4b4=a5b5,则可推出:

∠p3=∠Q3=∠p4=∠Q4=∠p5=∠Q5。

所以当机器人整体在弯道内可以运动的条件是:

(3)

式中,F14,f14—— 弯道内前部分推力、摩擦力

F24,f24—— 弯道内后部分缩回力、摩擦力

Q4—— 前部分推力与摩擦力夹角

p4—— 后部分缩回力与摩擦力夹角

以机器人在管道直道部分滑动摩擦力为5 N为例,分析了机器人在管道内的摩擦力变化,如图4所示。前锥形垫、后锥形垫在直道内的摩擦力为5 N,在过渡处后锥形垫的摩擦力为5 N,前锥形垫摩擦力逐渐减少,当整体进入弯道,前后锥形垫的摩擦力相等,都为摩擦力最小值。

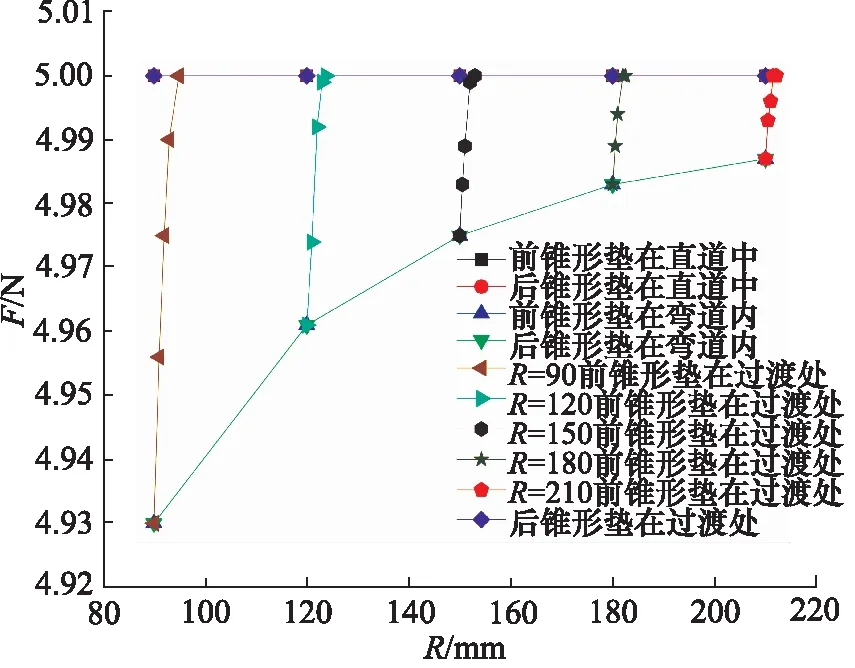
图4 前、后锥形垫摩擦力与拐弯半径关系Fig.4 Relationship between friction and bending radius of front and rear cone pads

从图4可得,拐弯半径越大,在过渡处的摩擦力越大,由于管道机器人利用摩擦力运动,而这也限制了目前管道机器人的拐弯半径。当拐弯半径足够大时,过渡处摩擦力便趋近于直道摩擦力。

2.2 转弯特性分析

机器人通过90°的直角弯道时,对机器人的要求最高[18]。分析几何约束条件时,将机器人近似于一个圆柱体。如图5a所示。在拐弯中有两种情况如图5b和图5c所示,分别为长度超过极限长度、直径超过极限直径。

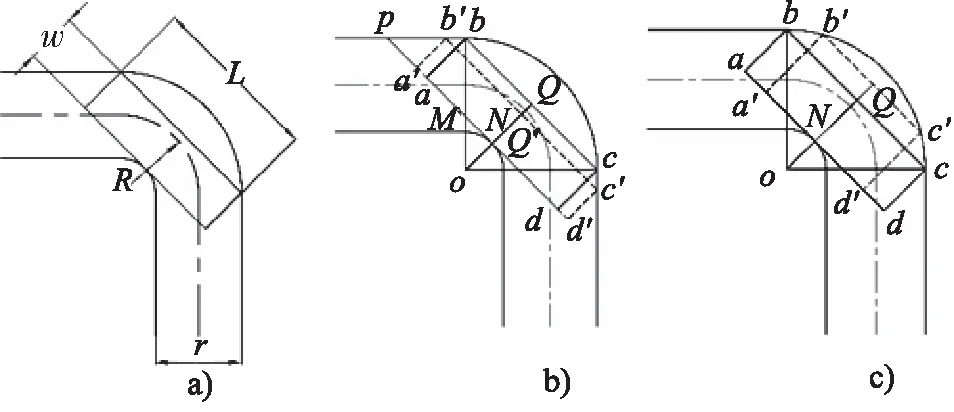
图5 转弯特性分析Fig.5 Analysis of turning characteristics

1) 长度超过极限长度

此时长度与直径应当满足:

(4)

式中,W—— 机器人直径

R—— 管道弯曲半径

r—— 管道内径

L—— 机器人长度

2) 直径超过极限直径

此时长度与直径应当满足:

(5)

已知机器人的最大长度是49+10=59 mm,管道内径为12 mm,带入式(5)可求得最小拐弯半径R约为70 mm。

当给定机器人的长度L分别是29,39,49,59 mm 时,图6展示了不同机器人直径W下的最小拐弯角度:

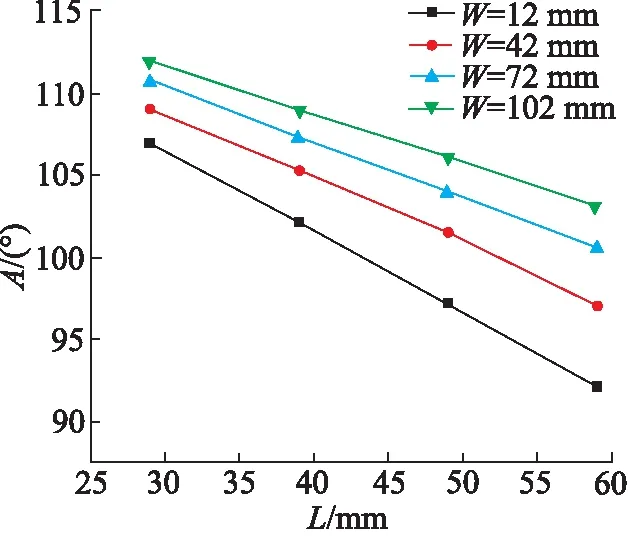
图6 机器人最小拐弯角度与长度、直径之间关系Fig.6 Relation between minimum turning Angle and length and diameter of robot

可知,当机器人的长度一定时,直径越大, 拐弯角度越大;直径一定时,长度越大,拐弯角度越小。

2.3 负载能力

机器人在管道内运动要携带小型摄像头,因此需要负载能力。而负载能力与机器人的自身属性与管道间的摩擦力等有关。

管道机器人前部分克服负载重力G与摩擦力f1,向上运动,当前部分上升后,重力G与摩擦力f1应当小于fmax,而后,后部分向上运动,完成一次周期内的上升。即有负载的运动条件为:

(6)

式中,F1 —— 前部分推力

f1 —— 前部分摩擦力

从式(6)可知,机器人在管道内的负载能力与机器人的前部分推力F1有关,F1由气压决定,图7展示了以气压p=0.5 MPa为基准的气压与负载关系。

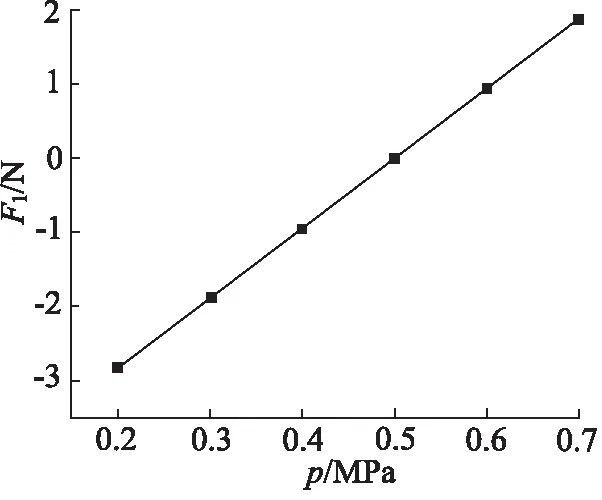
图7 机器人负载能力与气压关系Fig.7 Relationship between robot load capacity and air pressure

3 实验原理与系统

管道控制系统由气泵,电磁阀,继电器,电源和机器人组成。其中气泵作为动力源,为机器人提供动力。电磁阀作为控制中介连接机器人和气泵,同时电磁阀与继电器相连,继电器与电源相连。继电器通过改变电路通断,控制电磁阀的开关,从而实现管道机器人气的通断,实现自身的伸出与缩回。

摩擦力的大小是机器人能否前进的重要因素。如图8所示为摩擦力实验装置示意图,该系统由控制系统、力传感器、信息采集系统组成。机器人在管道内的运动由气泵、电磁阀、继电器和电源组成,通过改变电磁阀的通断控制机器人的运动,锥形垫固定在机器人的伸出部分,当机器人在管道内运动时,信息采集系统便可以采集到摩擦力数据。实验装置如图9所示。

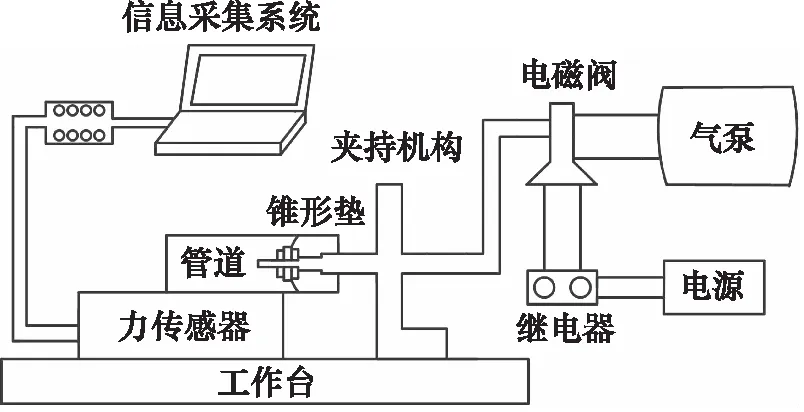
图8 实验系统原理Fig.8 Principle of test system

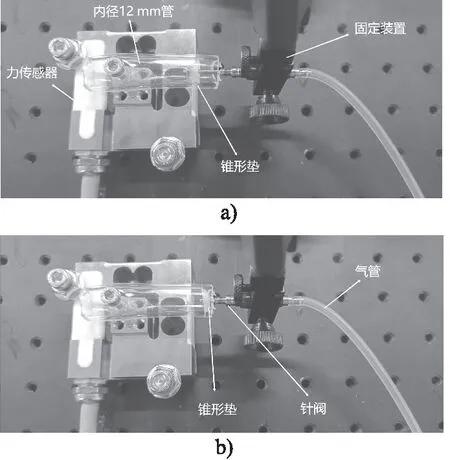
图9 测量摩擦力系统Fig.9 Measurement of friction system

机器人在管道内探测,需要携带摄像头,因此需要一定的负载能力。如图10所示为机器人的负载实验,机器人在气压p=0.5 MPa,频率f=1的条件下,负有负载向上运动。

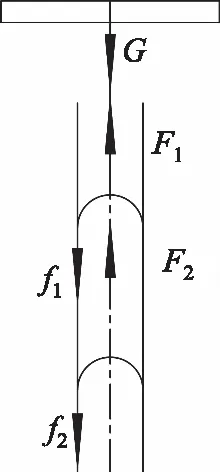
图10 测量负载系统Fig.10 Measuring load system

4 实验分析

由图11对比图9可知,伸长最大静摩擦力对应从图9b到图9a运动过程中,锥形垫翻转所需要的力;缩回最大静摩擦力fmax对应图9a到图9b运动过程中,锥形垫翻转所需要的力;伸长滑动摩擦力对应图9a到图9b,锥形垫翻转后在管道内运动的摩擦力。

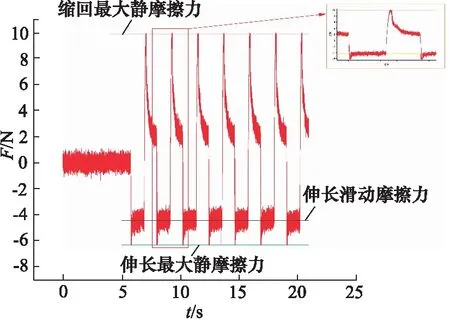
图11 摩擦力数值Fig.11 Values of friction force

经计算可得伸长最大静摩擦力为4.74 N,缩回最大静摩擦力fmax为6.76 N,伸长滑动摩擦力为3.45 N。

由图3及表2可知,oa′=ob′,a′b′=10,求得∠Q′=∠p′=4.13°。

带入式(1)～式(3),可知均满足机器人在管道内的运动条件。

如图12所示,管道内径为12 mm,弯曲半径约为150 mm。

图12所示,a阶段为实验开始阶段,机器人整体在直道内; b阶段为机器人在直道内运动若干个周期后的位置; c阶段为机器人运动到过渡处; d阶段为机器人整体运动到弯道处; e阶段为机器人穿过弯道,运动到直道;

可得,机器人可以顺利通过拐弯半径150 mm的弯道。

如图13所示,机器人末端和螺杆之间连接, 将100 g砝码固定于螺杆,机器人与负载一同向上运动,即为机器人的负载实验。图14为螺杆等其他零部件重量。

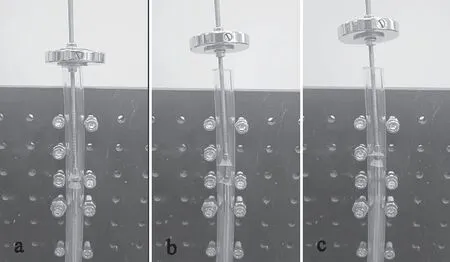
图13 负载实验Fig.13 Load experiment

如图13所示,a阶段为机器人带有负载在竖直管道内运动的开始阶段,此时砝码底面与管道末端重合,红色标记为起始点;b阶段为机器人向上运动到第二个周期的伸长阶段,c阶段为机器人经过若干个运动周期后的位置,可看出,机器人相比较图a阶段有了明显的上升,证明机器人可负载约124.5 g负载运动。

由式(7)知机器人最大负载为1.25 N。由实验得,机器人负载约为1.22 N,与数据基本相符。

5 结论

(1) 机器人在管道内的摩擦力由锥形垫与管道共同决定,通过改变锥形垫与管道的材质、尺寸可以改变摩擦力;

(2) 提出了一种适用于管道探测的气动柔性机器人,机器人最大长度59 mm,最大直径处13 mm,适用于内径12 mm、拐弯半径70 mm以上的管道,理论上通过改变锥形垫的直径可以适应不同直径的管道;

(3) 对管道机器人的运动特性、拐弯特性做了分析,并且给出了对应的数学模型;

(4) 对设计的管道机器人做了负载分析,可得机器人负载与本身质量比约为10。