多通道振动信息融合的柱塞泵异常检测方法

鲁思杰, 潮 群,2, 刘成良

(1.上海交通大学 机械系统与振动国家重点实验室, 上海 200240;2.浙江大学 流体动力与机电系统国家重点实验室, 浙江 杭州 310027)

引言

液压系统具有结构紧凑、传动平稳和功率密度高等优点,被广泛地应用于工业生产、航空航天和海洋工程等领域[1]。然而,复杂的系统结构、多变的负载条件和恶劣的使用工况等因素也给液压系统的运行和维护带来了巨大的挑战。 而且, 液压系统的故障类型多样,一旦发生,轻则影响设备正常运行,延误生产计划和工程进度;重则引发生产事故,造成人员伤亡和财产损失。所以,对于液压系统进行状态监测和故障诊断研究具有重大意义,能够极大程度地提升系统整体的可靠性和安全性[2-3]。

作为液压系统的核心部件,柱塞泵是状态监测和故障诊断的重要研究对象。传统的柱塞泵故障诊断方法非常依赖专家经验知识,并且受限于故障模式的特征提取[4]。为了解决该问题,ZHU Yong等[5]基于深度学习理论,将小波分析与改进后的卷积神经网络(Convolutional Neural Network, CNN)相结合,提出了一种新的柱塞泵智能故障诊断方法。相比于经典的AlexNet,该方法通过修改神经网络的结构降低了参数数量和计算复杂度,所构建的模型充分融合了小波分析的特征提取能力和卷积神经网络的表征学习能力。针对传统机械故障诊断方法依赖大量信号处理技术和在数据预处理方面耗时的问题,ZHU Yong等[6]使用粒子群优化算法(Particle Swarm Optimization,PSO)对改进LeNet-5模型的超参数进行自动优化,在一定程度上减少了模型修改和训练的时间,最后通过所构建的模型对柱塞泵正常状态、斜盘磨损、滑靴磨损、滑靴松动和中心弹簧失效等五种状态进行了分类识别,达到了98.71%的准确率。TANG Shengnan等[7]开发了一种使用批量归一化策略的卷积神经网络框架,并且通过同步小波变换进行故障特征的提取,最终在有效应对数据分布变化问题的同时实现了液压柱塞泵的故障诊断。姜万录等[8]将平衡随机森林算法(Balanced Random Forest,BRF)应用于轴向柱塞泵的故障诊断,提高了类间数据不均衡条件下故障分类的精确度。基于迁移学习,HE等[9]在用于轴向柱塞泵故障诊断的对抗模型中添加了多信号融合模块,对振动信号和声信号进行权重分配,从而提高了该方法在柱塞泵跨域故障检测中的性能。杜名喆等[10]使用经验小波变换对柱塞泵振动信号进行预处理,然后以峭度值作为内禀模态函数的分量标准,并且通过卷积神经网络对该分量进行分类,从而实现了柱塞泵的故障诊断。吴主金等[11]通过多项式Chirplet变换和变分模态分解相结合的诊断方法,实现了变转速工况下柱塞泵故障特征的提取。TANG Shengnan等[12]采用自适应学习率策略建立深度卷积神经网络模型,将柱塞泵振动信号、压力信号和声音信号的时频信息作为模型输入,最终能够准确地识别出液压柱塞泵的各种故障。

但是在实际的工程应用中,轴向柱塞泵的故障诊断并不是使用者最期望的,对于工程机械等领域,一旦柱塞泵发生了故障,工作人员往往会停止整个液压系统的工作,并且更换柱塞泵,而不是在确定柱塞泵的故障原因后进行检修,因为柱塞泵本身作为易损件,整体更换的成本和效率往往要优于拆卸维修。因此,及时准确地检测出柱塞泵的异常状态,从而尽早采取相应措施,避免整个液压系统由于单个柱塞泵的异常而发生损坏,这在工程实践中具有重要意义。对于轴向柱塞泵,目前的研究内容主要集中于故障诊断和状态监测等方面,异常检测的相关内容较少。为此,本研究提出了一种无监督式机器学习的柱塞泵异常检测方法,对柱塞泵壳体上多个方向的振动信号进行融合,利用变分自编码器提取柱塞泵健康状态下振动信号融合后的特征,从而对柱塞泵的异常状态进行检测,最后通过柱塞泵在16种工况和3种故障状态下的振动信号进行测试。

1 小波变换

传统的信号处理方法以傅里叶变换为基础,其实质为将满足特定条件的信号表示为不同基频的谐波函数的线性叠加。作为一种线性积分变换,傅里叶变换被用于信号在时域和频域之间的转换。但是,对于非平稳和突变信号,傅里叶变换存在局限性。而且,作为一种全局性的变换,傅里叶变换不具备局部化的分析能力。对于液压系统,传感器所采集信号的局部特征通常会包含设备状态的关键信息,例如,状态监测特别关注突变信号的功率谱密度估计。为了弥补这一缺陷,可以在傅里叶变换中添加滑动窗口,这样就变成了短时傅里叶变换。然而,因为滑动窗口是确定的,其大小的选取又造成了新问题:滑动窗口太窄会使得信号太短,导致频率分辨率不足;而滑动窗口太宽,又会导致时间分辨率低。虽然增加滑动窗口可以凸显信号变换后的局部特征,但是窗口内不同的谱分量被平均,所以对突变信号不敏感,容易会丢失信号中的短时、高频成分。

作为一种新的信号分析方法,小波变换(Wavelet Transform, WT)继承和发展了短时傅立叶变换的局部化思想,滑动窗口的宽度可以随着频率的增加而减小,克服了窗口大小无法跟随频率变化的缺点。对于信号f(t),其连续小波变换(Continuous wavelet transform, CWT)为:

(1)

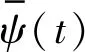
(2)

之所以需要满足“可容许条件”,是为了确保小波变换的可逆性。而且,ψ(t)∈L2(R)是均值为0的有界函数,需要被归一化,如下述公式所示:

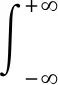
(3)

(4)

通过母小波函数的伸缩和平移性质,小波变换可以对信号进行多尺度的细化,进而实现在高频时细分时间,在低频时细分频率。基于该性质,小波变换非常适合于检测信号中的异常,被广泛应用于机电液系统的状态检测和故障诊断。

2 自编码器

2.1 自编码器

自动编码器(Autoencoder, AE),简称自编码器,是一种前馈非循环神经网络,由Rumelhart等人首次提出[13]。自编码器将输入数据作为学习目标,以尽可能小的误差对其进行重建。作为一种无监督的机器学习方法,自编码器具有优秀的数据维度压缩和数据特征提取能力,在图像处理、机器翻译、信息检索等方面有着广泛的应用。此外,由于能够产生与输入数据类似的数据,自编码器也被用于数据增强和神经网络的预训练。与其他神经网络相同,自编码器也是通过反向传播算法(Back-Propagation, BP)来优化自身权重从而进行学习。自编码器的独特之处在于其网络结构中存在瓶颈层(Bottleneck),该瓶颈层中的隐藏变量就是输入数据被压缩提取后的表示。编码器、瓶颈层与解码器三者共同组成了自编码器。对于输入数据xi,编码器对其进行映射:

h=g(xi)

(5)

其中,h∈q为编码器的输出,即输入数据在瓶颈层的表示,g:n→q。编码器的作用是把高维度的输入数据xi编码为低维度的表示(中间变量)h,从而使得自编码器学习最有信息量的特征。同样,解码器对瓶颈层的表示再次进行映射:

(6)

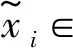
(7)

其中,Δ代表对于自编码器输入输出差异的度量,通常采用均方方差(Mean square error, MSE)表示,〈〉代表者对于所有自编码器的输入取平均。对于所有参与训练的输入数据xi,映射g(·)和f(·)应该使输出数据xi与其差异的平均值最小。自编码器自身的权重能够进行共享,即编码器和解码器的权值互为转置,这样可以加快网络训练的速度,但同时也降低了网络的灵活程度。

2.2 变分自编码器

变分自编码器(Variational autoencoder, VAE)被认为是深度学习领域中最具有研究价值的无监督式学习模型,其理论来源于贝叶斯变分推断[14]。与基础的自编码器相比,变分自编码器对于数据特征的提取能力有了巨大的提升[15]。从网络结构来看,变分自编码器与基础的自编码器是一样的,也包含编码器和解码器两个部分,解码器将高维度的输入映射到低维度的隐藏变量,编码器将隐藏变量重新映射到高维度,两者之间的差异在于,变分自编码器对于输入数据编码后的隐藏变量不再是以张量的形式表示,而是通过概率分布来表示。

本质上,普通自编码器在训练过程中学习的是输入数据与隐藏变量之间的映射关系,是一种不涉及概率的确定性判别模型,而变分自编码器在训练过程中试图通过概率分布描述输入数据的生成过程,是一种使用概率的随机生成模型。变分自编码器由所谓的概率有向图模型构成(Directed Probabilistic Graphical Model,DPGM),图1展示了典型的概率有向图模型。

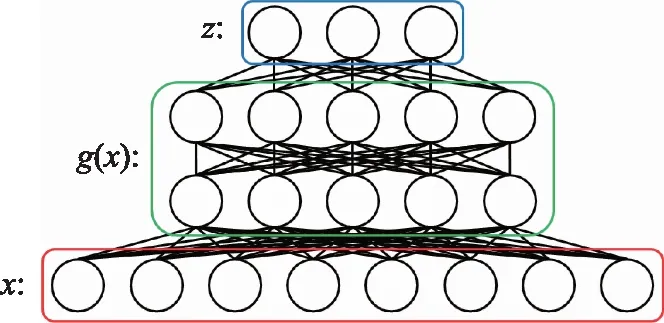
图1 概率有向图模型Fig.1 Directed probabilistic graphical model

在变分自编码器中,概率有向图模型最上层为隐藏变量所在处,也是生成过程开始处。变分自编码器中的生成过程从隐藏变量z开始,g(z)代表生成数据x的过程,该过程通过神经网络建模。变分自编码器的目标函数为数据边缘似然的变分下界,该边缘似然为对所有数据边缘似然求和:

(8)

其中,各个数据的边缘似然为:

logpθ(xi)=DKL(qφ(z|x)‖pθ(z))+(θ,φ;xi)

(9)

其中,qφ(z|x)为近似后验,pθ(z)为隐藏变量z的先验分布。DKL(qφ(z|x)‖pθ(z))为Kullback-Leibler(简称KL)散度的近似后验和先验,(θ,φ;xi)为数据xi边缘似然的变分下界。因为KL散度始终大于0,所以公式可以写为:

logpθ(xi)≥(θ,φ;xi)

=Eqφ(z |xi)[-logqφ(z|x)+logpθ(x|z)]

=-DKL(qφ(z|xi)‖pθ(z))+

Eqφ(z |xi)[logpθ(x|z)]

(10)

给定隐藏变量z,pθ(x|z)为数据x的似然。-DKL(qφ(z|xi)‖pθ(z))为隐藏变量z近似后验和先验之间的KL散度。该项使得隐藏变量z的后验分布与先验分布近似,为降低算法泛化误差的正则项。Eqφ(z |xi)[logpθ(x|z)]则根据后验分布qφ(z|xi)和似然pθ(z)对输入x进行重建。

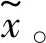
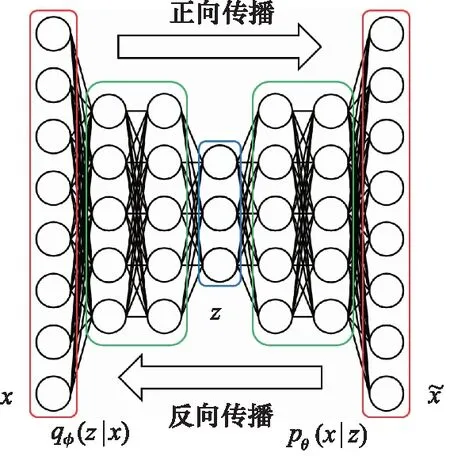
图2 变分自编码器整体结构Fig.2 Overall structure of variational autoencoder

变分自编码的训练使用反向传播算法。式(10)中最后等式右侧的第二项应该通过蒙特卡洛方法计算,但是传统的蒙特卡洛梯度法用于优化变分下界时会存在非常高的方差,因此并不适用[16]。为了避免这种情况,变分自编码器使用了重参数化技巧,即使用标准正态分布中的随机变量替代原始分布中的随机变量。随机变量z通过变换hφ(ε,x)重参数化,其中ε来自标准正态分布,即:

(11)

3 无监督学习的柱塞泵异常检测方法

针对柱塞泵异常状态实时报警的需求,提出了一种可以在多种工况下使用的异常检测方法,该方法的实现流程如图3所示。

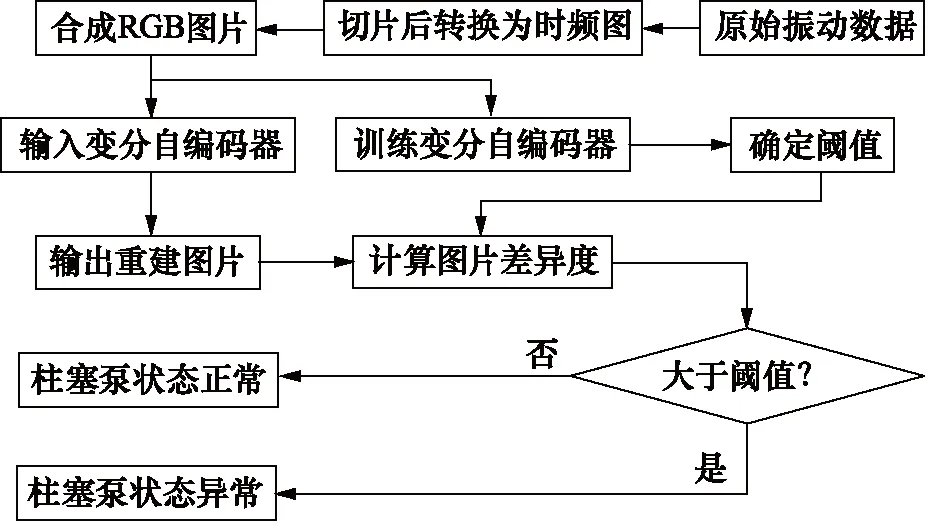
图3 柱塞泵异常检测算法实现流程图Fig.3 Flow chart of piston pump anomaly detection algorithm

异常检测方法的流程为:

(1) RGB图片合成。该异常检测方法需要采集柱塞泵壳体上轴向、法向和切向的振动信号,然后分别对其切片, 确保每一个信号片段中均包含柱塞泵运转一周的完整波形,然后选用合适的母小波函数,对这些信号片段分别进行连续小波变换,获得三个方向振动信号的时频图。因为初始时频图的尺寸过大,不利于后续输入到变分自编码器中,所以需要对其进行降采样处理,使得时频图的最终尺寸为128×128像素;对降采样后的时频图再进行归一化处理,使得所有像素点的取值范围为[0,1]。根据RGB色彩模式,分别将处理后的轴向振动信号时频图、法向振动信号时频图和切向振动信号时频图输入到红(Red)、绿(Green)、蓝(Blue)三个颜色通道,合成RGB彩色图片。

(2) 变分自编码器训练。以柱塞泵健康状态下轴向、法向和切向振动信号所合成的RGB图片作为基准,通过反向传播算法对变分自编码器进行训练。变分自编码器中使用了卷积神经网络来提高对图像特征的提取能力,通过选取合适的卷积核个数、卷积核大小和卷积层数,使得训练后变分自编码器对于图像的重建能够达到最好的效果。同时,为了避免训练时产生过拟合问题,在变分自编码器中引入了批标准化(Batch Normalization, BN)正则化方法。在不同转速和负载压力下,使用相应的RGB图像进行变分自编码器的训练。对于变分自编码器输入和输出的图片,使用欧式距离衡量两者差异度。在训练阶段,记录所有RGB图片重建前后差异度,然后根据拉依达准则对这些数据进行离群值处理,最后选取其中的极大值作为后续异常检测的阈值。

(3) 实时异常检测。将实时采集的柱塞泵轴向、法向和切向振动信号合成为RGB图片,输入训练后的变分自编码器进行图片重建,根据图片重建前后的误差来判断柱塞泵是否出现异常,当误差大于阈值时,则认为柱塞泵出现了异常。

4 试验验证

4.1 试验台搭建与试验方案

为了验证所提出的异常检测方法是否可以对柱塞泵的异常状态进行准确有效的检测,通过柱塞泵故障模拟试验台采集柱塞泵在不同状态下的振动数据,从而进行验证。柱塞泵故障模拟试验台如图4所示,由数据采集单元、控制单元和被测泵三部分组成。试验中所使用的柱塞泵为A10VSO71开式泵,是一种斜盘式轴向变量柱塞泵,应用于开式回路。图5为整个试验系统工作回路的原理图。在柱塞泵外壳上安装了江苏东华测试技术公司生产的三轴加速度传感器1A313E,用于采集柱塞泵壳体上轴向、法向和切向的振动信号。传感器信号的采集使用NI-9234采样卡,其最高采样频率可以达到51.2 kHz,分辨率为24位,动态范围为102 dB。

图4 柱塞泵故障模拟试验台Fig.4 Piston pump failure simulation test bench

1.油箱 2.比例溢流阀 3.流量计 4.过滤器 5.压力传感器 6.被测泵 7.扭矩/转速传感器 8.电机 9.补油泵 10.加热器 11.温度传感器图5 试验台液压原理图Fig.5 Hydraulic schematic diagram of test bench

该试验过程不仅需要采集柱塞泵健康状态下的振动信号,还需要采集柱塞泵在不同故障模式下的振动信号。柱塞泵由配流盘、缸体、柱塞、滑靴、斜盘等零部件构成。根据柱塞泵的常见失效模式,在零件表面加工划痕来模拟柱塞泵典型故障形式,包括缸体磨损、滑靴磨损和柱塞磨损,如图6所示。缸体磨损通过在缸体端面加工三道周向划痕进行模拟,滑靴磨损通过在滑靴底面上加工两条不通过油室的划痕、一条贯穿油室的划痕进行模拟,柱塞磨损通过在表面加工四道轴向划痕进行模拟。为了验证提出的异常检测算法适用于多种工况,通过改变测试泵转速和压力,获得16种工况下的振动数据,如表1所示。

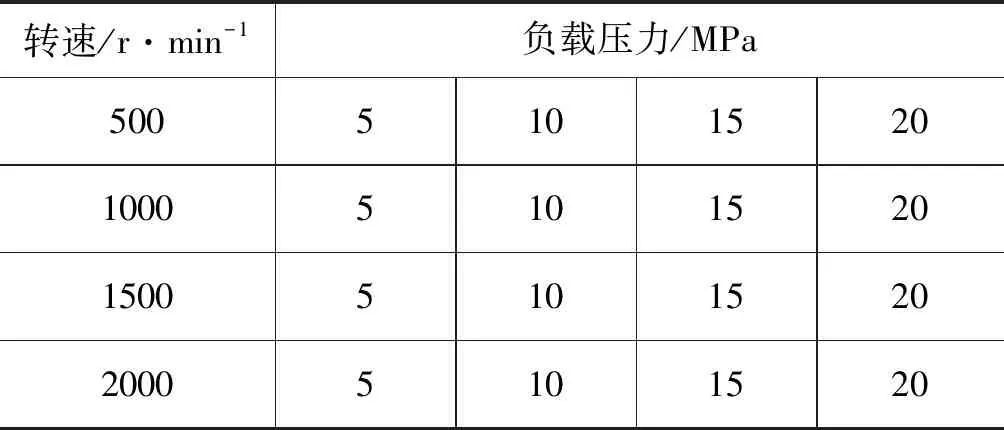
表1 试验工况Tab.1 Test conditions

图6 通过加工划痕来模拟故障的零件Fig.6 To simulate faulty parts by machining scratches

4.2 试验数据集

通过试验采集了柱塞泵在16种工况、4种状态下的三轴振动信号,总共64组数据。图7展示了在2000 r/min转速和20 MPa负载压力下,柱塞泵处于不同状态时三轴振动信号的时域波形图,图中只展示了柱塞泵转动一圈所产生的振动信号。采样频率相同,由于柱塞泵在不同工况下的转速不同,所以柱塞泵转动一圈所采集的信号点数也不同。为了尽可能降低计算量和提高时效性,异常检测算法所需要的输入数据均为柱塞泵转动一圈的采样点数。柱塞泵在不同工况和不同状态下的振动信号都需要按照前述流程进行相应的处理,最终合成为RGB图片。最终,在柱塞泵的每种工况和状态下,都有100张128×128像素的RGB图片,总计6400张。在训练变分自编码器时,使用正常状态下合成的RGB图片,在测试异常检测算法时,使用三种故障模式下合成的RGB图片。

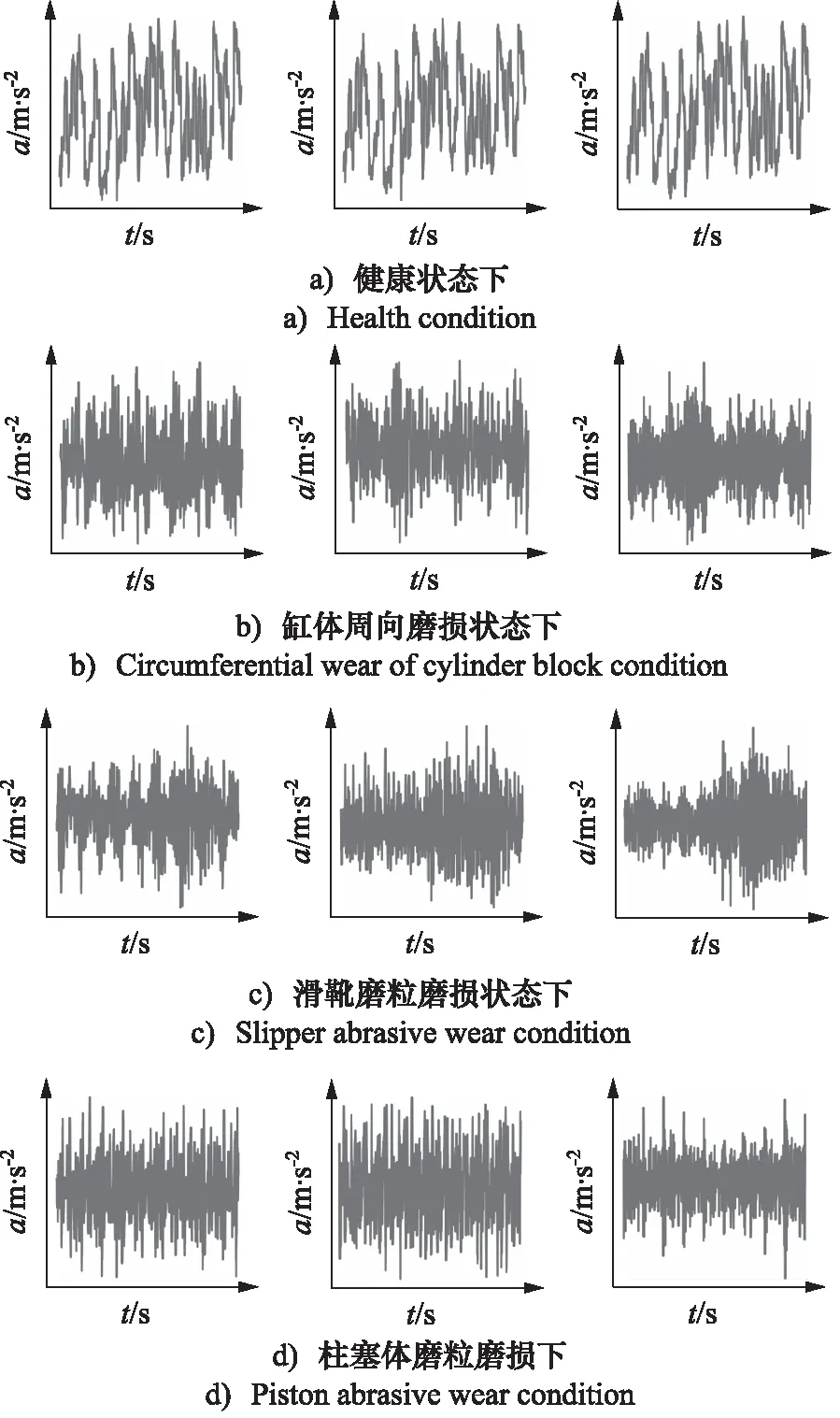
图7 不同状态下柱塞泵的三轴振动信号Fig.7 Triaxial vibration signals ofaxial piston pump under different conditions

4.3 异常检测结果分析

在每种工况下,对柱塞泵正常状态下合成的RGB图像进行划分,随机选取其中的80%作为训练集,其余的20%作为验证集。在使用训练集完成变分自编码器的训练之后,利用验证集进行验证。在使用变分自编码器的图片重建能力来实现柱塞泵异常检测时,使用图片重建前后的差异度作为异常判定的标准。对于重建后的图片,计算其与原图片的欧氏距离,然后除以图片的总像素点数来归一化,使得该数值的取值范围为[0,1],最终作为重建差异度。为了确定柱塞泵异常检测算法的异常状态判定标准,统计所有测试集和验证集中RGB图片重建前后的差异度,然后根据拉依达准则去除其中的异常值,选取去除异常值后的最大值,将其作为异常检测的阈值,进行异常判定。在不同转速和负载压力下,异常检测的阈值如图8所示。从图中可以看出,在同一转速条件下,负载压力的大小会影响异常检测阈值的大小,在负载压力相同时,异常检测阈值也会受到转速的影响。整体来看,不同工况下异常检测阈值的变化较小。

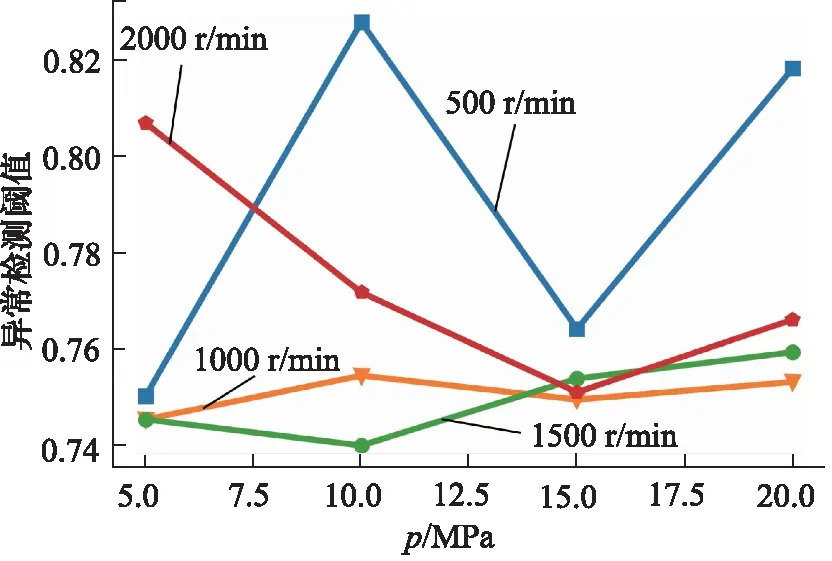
图8 不同工况下的异常检测阈值Fig.8 Anomaly detection thresholds under different working conditions

为了验证所提出的轴向柱塞泵异常检测算法的异常检测性能,将所提出的算法(CWT-VAE)与使用自编码器替换变分自编码器(CWT-AE)的异常检测算法进行对比,两种算法在不同工况下对于缸体磨损、滑靴磨损和柱塞体磨损的异常检测准确率分别记录在表2和表3中。对比2张表格可知,使用变分自编码器进行异常检测时,在500 r/min转速和5 MPa负载压力的工况下,异常检测的准确率较低,即算法无法检测出三种故障模式所导致的柱塞泵异常;但是在其他工况下,对于三种故障模式所导致的异常,算法检测的准确率基本都可以接近100%。而在使用自编码器进行异常检测时,在多数工况下,针对三种故障模式所导致的异常,算法检测的准确率都处于不太高的状态。这很好地说明了:在多数情况下,相比于自编码器,变分自编码器对于图像特征的提取能力更加优异,能够以更小的误差来重建图像。在500 r/min转速和5 MPa负载压力的工况下,算法的异常检测性能低下,并且从图8中可以看出在500 r/min转速时,不同负载压力下的异常检测阈值存在一定的波动,此时柱塞泵三种故障模式的特征并未较好地体现在振动信息融合后的RGB图像中,从而导致变分自编码器未能较好地进行特征学习。因此,低转速工况下柱塞泵不同故障模式的特征提取将作为后续的研究方向。

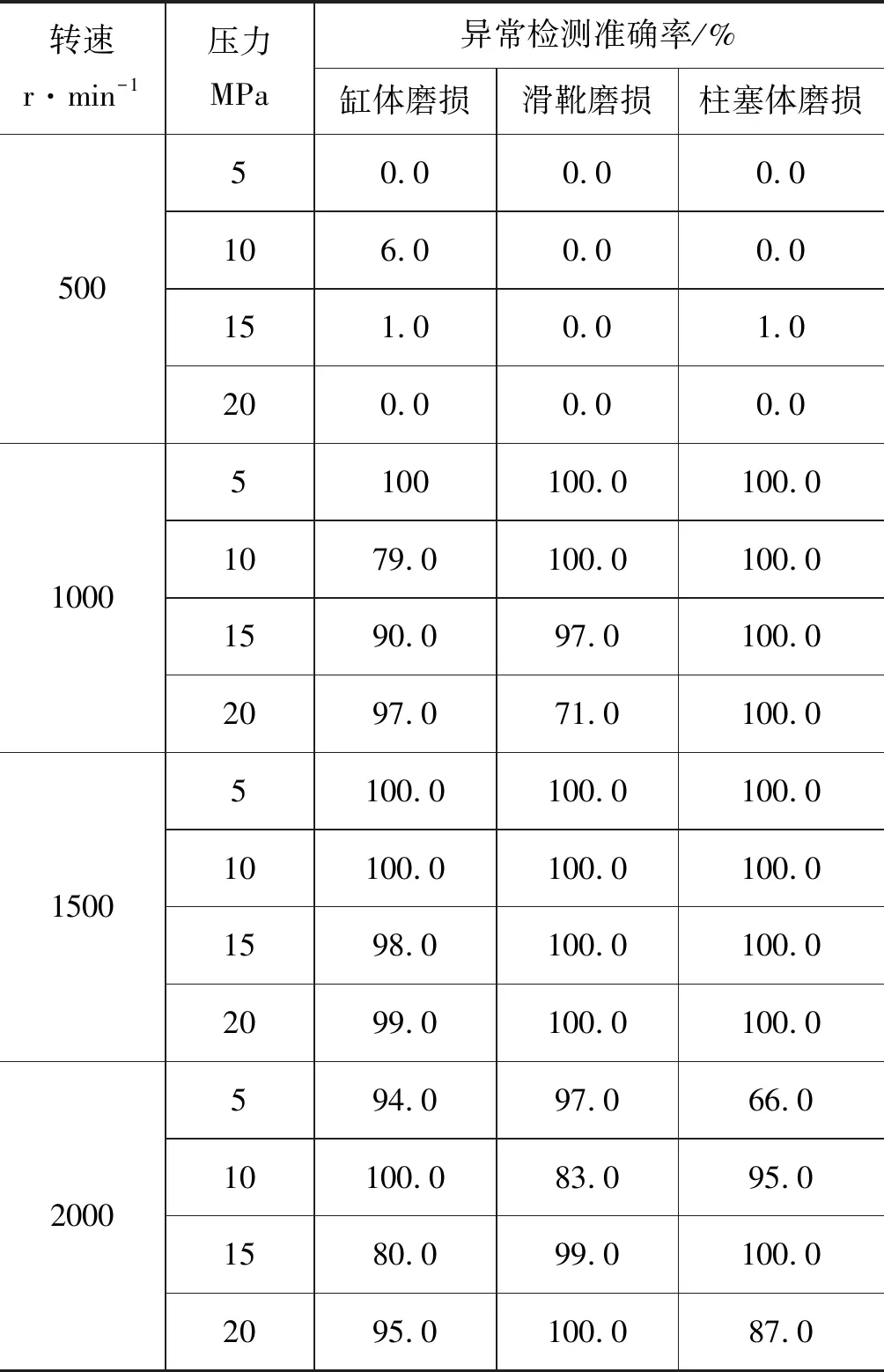
表2 CWT-VAE的异常检测准确率Tab.2 Anomaly detection accuracy of CWT-VAE

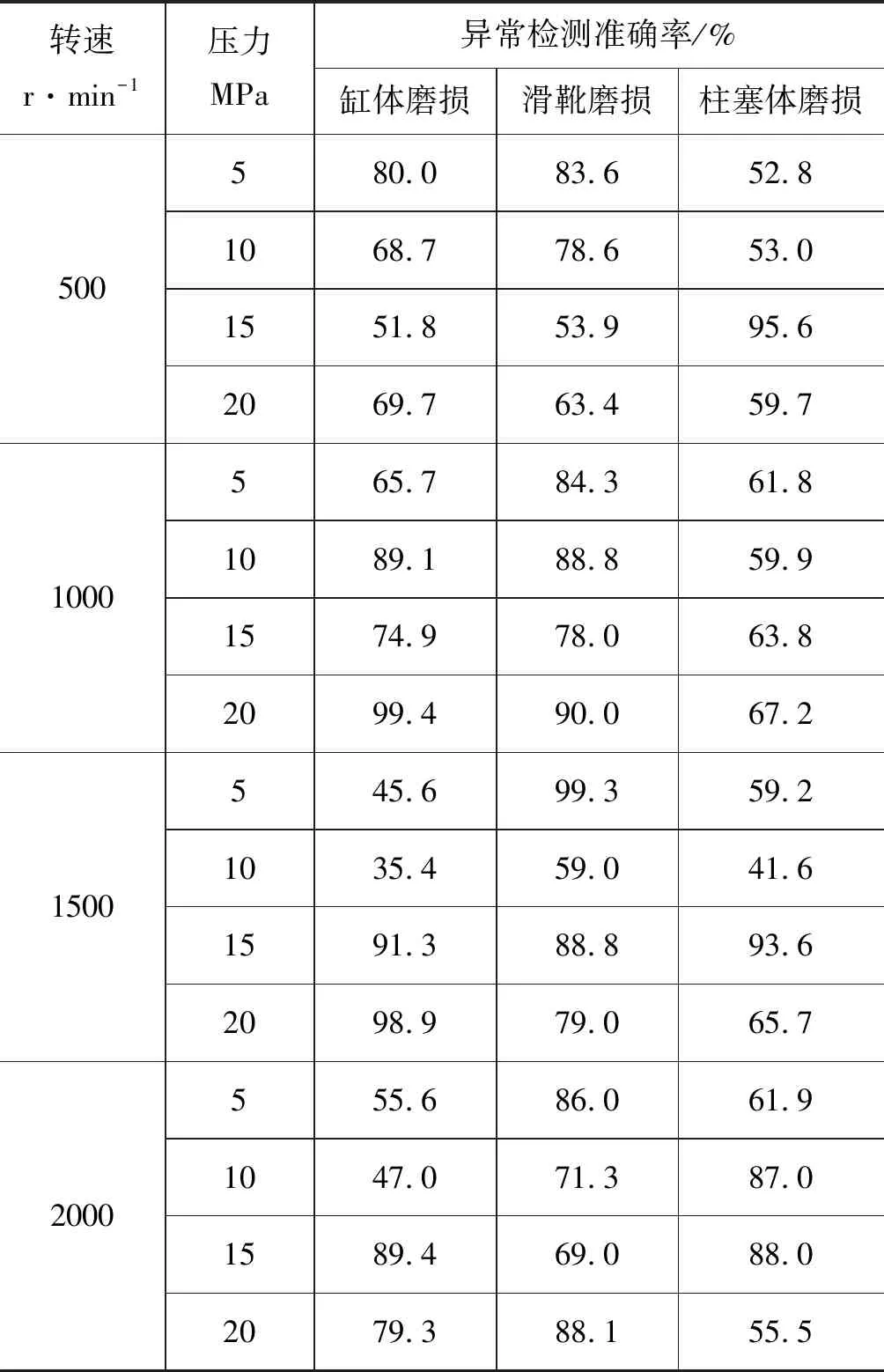
表3 CWT-AE的异常检测准确率Tab.3 Anomaly detection accuracy of CWT-AE

在转速为1500 r/min、负载压力为5 MPa的工况下,使用变分自编码器进行异常检测时,柱塞泵正常状态和柱塞体磨损状态下三轴振动信号所合成RGB图片的重建差异度分布如图9和图10所示,从图中可以看出,RGB图片经过变分自编码器重建的差异度基本符合正态分布,并且正态分布的主峰与异常检测阈值之间保持了一定的距离,表明所提出的异常检测算法已经较好地学习了柱塞泵柱塞体磨损状态下三轴振动信号的时频特征,实现了柱塞泵正常状态和柱塞体磨损状态之间的区分,提高了异常检测的准确性和鲁棒性,具有一定的工程应用价值。

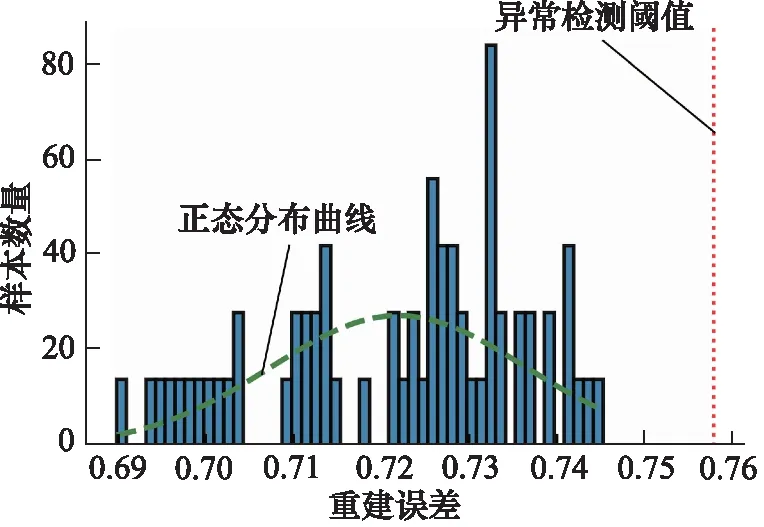
图9 正常状态下图片重建差异度分布Fig.9 Image reconstruction variance distribution under normal state

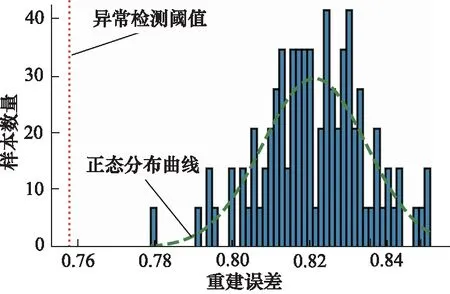
图10 柱塞体磨损状态下图片重建差异度分布Fig.10 Image reconstruction variance distribution under state of piston wear

5 结论

(1) 使用连续小波变换和变分自编码器的异常检测方法基于数据重构这一过程,将柱塞泵三轴振动信号的时频图进行融合,输入变分自编码器,结合批标准化正则化方法进行模型的训练,提取融合后图像的特征,进而具备重建图像的能力,通过图像重建差异度与阈值的关系来判断是否出现异常。最后,利用柱塞泵在三种故障模式下的振动信号完成了柱塞泵异常检测算法的验证,证明了所提出异常检测算法的有效性和准确性。

(2) 相比于使用普通自编码器进行不同工况和不同故障模式下柱塞泵的异常检测,使用变分自编码器具有更好的效果,表明了变分自编码器在图像重建上的优越性。