在操作中培养学生的空间观念
齐铁清

摘要:数学深度学习离不开学生的动手操作,离不开问题的解决。数学教材中的拓展题是很好的教学资源,教师要引导学生积极思考,大胆尝试,通过摆一摆、画一画、切一切、拼一拼的方法,互相交流、共同探讨,在活动中学习,在操作中感受。
关键词:操作活动;空间观念;深度学习
空间观念是义务教育阶段学生数学核心素养的主要表现之一。空间观念主要是指对空间物体或图形的形状、大小及位置关系的认识。《义务教育数学课程标准(2022年版)》(以下通称“新课标”)在学段目标和课程内容中对学生空间观念的要求是一个循序渐进的过程:从形成初步的空间观念、形成空间观念、培养空间观念、发展空间观念、增强空间观念到提升空间观念。很多教师结合具体的教学内容来理解这些要求一般比较容易,但对于这些要求如何转化成学生的观念却方法不多。本文结合北师大版数学教材中三道拓展题的解决过程来阐述如何在操作中培养学生的空间观念。
一、有思维的操作:从用尺画角到用角度量
角的度量是北师大版数学教材四年级上册“线与角”这一单元中的一部分内容。教材在“旋转与角”“角的度量”的教学内容后安排了一道“用一副三角尺画不同度数角”的拓展题。通过对这道题的处理,可以看出教师对培养学生空间观念的理解、认识、落实程度。
(一)原题:用一副三角尺画不同度数的角
这是教材中的一道拓展题,原题是:“利用一副三角尺,你能画出哪些不同度数的角?”教材中给了提示:“我画了一个105°的角”“我画了一个15°的角”,并配了插图。
在实际教学中,教师一般情况下会根据这些提示,引导学生在三角尺原有的30°、45°、60°、90°的基础上,通过相加和相减的办法可以再画出75°、105°、120°、135°、150°、180°的角。
在这样的教学活动中,学生的思维基本上是停留在“利用原有的6个角通过加减的方式来画出新的角”这一阶段。
(二)原解:一共能画出11种不同度数的角
在北京师范大学出版社《义务教育教科书数学教师教学用书》(以下称为“教参”)中有对此题的说明:“本题是拓展题,不要求全体学生掌握。鼓励学生大胆尝试,先独立地摆一摆、画一画,再交流方法。答案:180°、150°、135°、120°、105°、90°、75°、60°、45°、30°、15°。”
教参中先是说明了此题的性质,然后提示了处理方式,最后给出了答案。从给出的答案中可以看出,是按照从大到小的规律排列的。
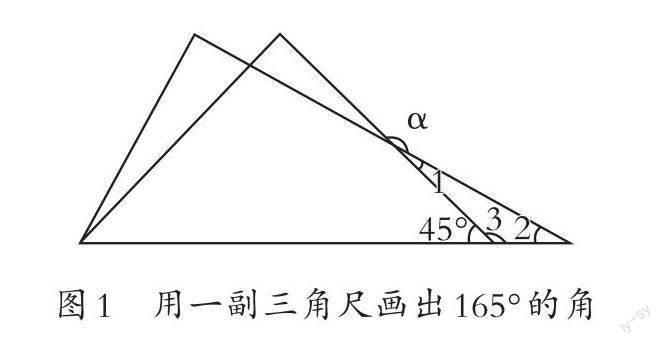
这样的答案并没有引起一些教师的注意,基本上是“以此为准”。如一位教师在引导学生归纳方法时对画出的角按照从小到大的顺序进行排序后发现,这些角度是有规律的,从15°开始,依次增加15°,一直到180°,但是中间缺少了165°。学生就此提出了疑问,并用一副三角尺画出了165°的角α(见图1),这个问题才引起大家的关注。
(三)原理:用工具画角是对角的重新量化
对于用一副三角尺能否画出165°角的讨论已经结束,但问题似乎并没有那么简单,其中有几个问题应该引起教师的关注。
第一个问题是:为什么一道题的答案有问题,在教参中存在这么长时间(现行版本是2014年版)却没被发现?第二个问题是:是什么原因导致了“不完美”的答案?第三个问题是:学生画出的这个165°角,其他学生是否认同?
第一个问题,主要原因为这是一道“拓展题”“不要求全体学生掌握”,那也就意味着不作考试要求。所以,一般情况下不对全体学生进行统一要求,即使是做出來的学生也不要求把所有的答案都写全。这样,也就没有人特别关注所有的答案了。
第二个问题,之所以没有给出165°的答案,主要是“成人化”“代数化”思维的结果。“利用一副三角尺你能画出哪些不同度数的角”一般理解为用一副三角尺中的两个不一样的三角尺已有的6个角相互拼摆来得到新的角。有些版本的教材在要求中也确实是说“能拼成哪些不同度数的角”。这样,没有165°的答案也就可以理解了。
第三个问题,有的学生并不认为这个165°的角是合理的,因为它不是利用三角尺原有的角画出来的。其实,这并不重要,重要的是这些角是学生“画”出来的还是“算”出来的。要是直接“算”,那是“算”不出165°的角的。
教师到此应该想到是一个问题:165°这个概念是怎么建立起来的?如果是拼角,那就需要有两个已经知道度数的角的和或差正好是165°才行。但如果是画角,那就需要看已经知道度数的最小的角是多少度,只要知道了这个度数,以它为单位,就可以画出它的倍数的所有的角了。而这正是度量的本质意义。
一副三角尺6个角的度数差最小是15°,那么就可以利用它来画出所有的15°的倍数的角,当然也包括165°。实际上,新课标中对学生“会用量角器或三角板画角”是有明确要求的,要求“会用三角板画30°、 45°、 60°、 90°的角”。这是因为三角板上有这些度数的角,如果学生能通过两个角的度数差来找到15°的角,那么画15°的角就很容易了。
有了这个基础,学生以15°为一个单位,就可以画出任意一个15°的倍数的角了。这样,得出来的是具有普遍意义的最基本的规律,它可以拓展,可以延伸。在学生学习角的时候就可以更好地理解角的形状、大小、位置关系了。
二、有意义的剪拼:从代数计算到几何直观
长方形的面积是北师大版数学教材三年级上册“面积”这一单元中的一部分内容。教材在这部分内容后面安排了一道“用一个大长方形能剪成几个小正方形”的拓展题。从这道题的解题过程中,可以看出学生对图形形状、大小、位置关系的理解程度。
(一)原题:一张纸能剪出多少个小正方形
这道拓展题的原题是:“王老师为小朋友准备了一张长32厘米、宽15厘米的长方形彩纸,最多可以剪成边长是2厘米的正方形彩纸多少张?”
这原本是一道没有多大难度的题,但解答这道题的思路却反映了学生对面积概念的理解程度。有的学生可能会把这题理解为“大长方形中包含几个小正方形”,从而用大长方形的面积除以小正方形的面积得到包含的个数。32×15=480(平方厘米),2×2=4(平方厘米),480÷4=120(张)。这是典型的“用代数思维解决几何问题”,不叫“数形结合”。
在这种情况下,教师可以引导学生动手做一做,在做中体会大长方形和小正方形之间的关系。通过操作,学生会发现,长方形的纸并不是正好用完,进而明白为什么不能剪成120张。
(二)原解:学生体会画图解决问题的方法
教参对此题的解释是“本题是拓展题,不作考试要求。练习时,可以先让学生画图,从图中可以直观地看出长的一条边能画16个,宽的一条边能画7个。体会画图解决问题的方法。答案:长边可以剪32÷2=16(份),宽边可以剪15÷2=7(份)……1(厘米),一共可以剪16×7=112(张)。”
对于这道拓展题来说,并不只是画图那么简单。关键是学生能否读懂原题,能否把原题还原成现实情境。教师应让学生真正动手进行操作,在操作中理解什么叫“用大的长方形剪成小的正方形”。
在操作中学生就会理解,题中要求最多可能剪成多少张,那就应该尽量用小的图形去密铺大的图形。这就会出现教参中提示的“长的一条边能画16个,宽的一条边能画7个”的情形。这个过程应该是先有操作再有算式,算式只不过是对操作过程的记录。如果没有对这些图形关系的认识,而只用算式来解释是没有意义的。
(三)原理:理解单位面积会更有实用价值
为理解这道题的用意,换一组数据也许效果会更好:“一个长6厘米、宽5厘米的长方形,最多可以剪成长3厘米、宽2厘米的长方形多少个?”
这道题无论是用算式计算还是画图操作,答案都是5(个)。但思考过程却完全不一样,用算式解决问题只能说明面积是30平方厘米的大长方形里面包含5个面积是6平方厘米的小长方形,不一定能形成裁剪方法的图形。而当学生自己能剪出5个小长方形时,他们对面积就有了一种新的认知:如果以长3厘米、宽2厘米的长方形的面积为一个“单位面积”(6平方厘米),那么长6厘米、宽5厘米的长方形中就有5个这样的“单位面积”(30平方厘米)(见图2)。
“单位面积”已经超出了学生对“面积单位”的固化理解。当学生已经习惯于用“一个面积单位”去度量面积的时候,就很难把“多个面积单位”当成“一个单位面积”去进行度量,更难理解用一个“不规则的单位面积”去进行度量。只有突破这种认知上的限制,学生才能真正理解面积的意义。
学生进而就会理解,有时一个大的图形虽然不能正好剪出几个完整的小图形,但是它们之间依然存在这种关系。如教材中的拓展题:“一张大的彩纸,最多可以剪成112张小彩纸。”但实际上如果以这张小的彩纸的面积为一个“单位面积”,那么大的彩纸的面积就有120个这样的单位。这种理解就不是就题解题,而是让学生在操作的过程中明白平面图形的形状、大小、位置关系。
三、有深度的转化:从体积单位到单位体积
学生对体积单位概念的建立往往不如长度和面积单位的建立那么“实在”,其原因主要是学生没有建立起“单位体积”的概念。从北师大版数学教材六年级下册一道拓展题的解题过程就可以看出学生对“单位体积”的理解程度。
(一)原题:用底面积乘以高计算柱体的体积
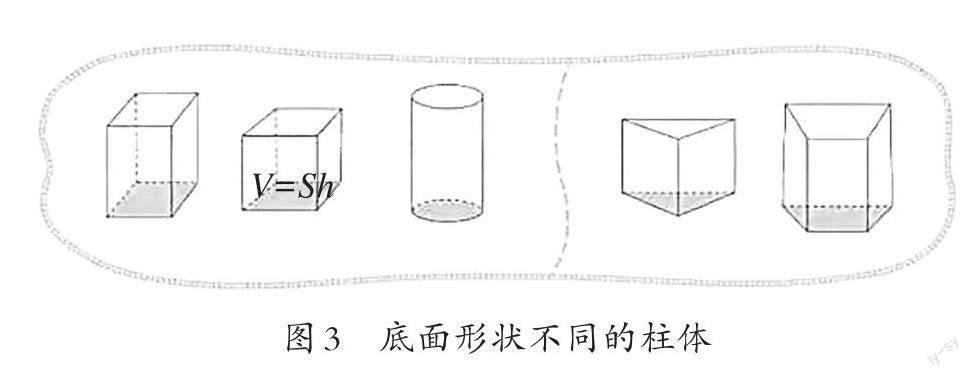
教材“圆柱与圆锥”这一单元中,在“圆柱的体积”后面有一道拓展题:“长方体、正方体和圆柱的体积都可以用V=Sh计算。想一想, 下图右面两个图形的体积也可以用V=Sh计算吗?说一说你的想法。”(见下页图3)
这样的拓展题,在教师看来并没有什么难度,也不会引起学生的关注。一般来说,解答时不会出现问题,都会回答“可以”。至于“说一说想法”,因为只是“说一说”,所以无非是“底面积乘以高可以求出长方体、正方体、圆柱体的体积,右面两个图形的底面也可以转化成长方形,从而把它们转化成长方体”之类的推理,教师在教学中不会太“较真”,也没有学生去操作,所以一般看不出什么问题。
(二)原解:利用转化的思想推出计算方法
教参中的解释基本意思是这样的:“本题为拓展练习,不要求全体学生掌握。主要引导学生思考、体会直柱体的体积都可以用V=Sh计算的理由。练习时,教师可以引导学生说说自己的思考方法,如可以用切、拼的方法,利用转化的思想,將图3中右面的两个图形转化为长方体,从而推出两个立体图形的计算方法。”
这个解释本身没有问题,但关键是学生是否真的能“思考”、是否真的能“体会”、是否真的知道“直柱体的体积都可以用V=Sh计算”的理由。更重要的是,学生能否由此真的能得出“直柱体的体积都可以用V=Sh计算”的结论。
(三)原理:理解体积就是度量单位的累加
新课标非常重视学生在数学学习过程中的操作,特别是在图形与几何教学中的测量与度量。在“教学提示”中提示教师“图形的认识与测量的教学要引导学生通过对立体图形的测量,从度量的角度认识立体图形的特征;理解长度、面积、体积都是相应度量单位的累加”。
学习体积的计算时,教材通过猜想验证的方式引导学生得出长方体体积的计算公式。让学生用一些棱长为1厘米的小正方体摆出3个不同的长方体,通过观察各自体积与长、宽、高之间的关系得出长方体体积的计算公式。包括底面积乘高的公式也是通过“底面积=长×宽”得出的。在这样的过程中,学生并没有“基于体积单位理解图形体积”,更没有“理解体积是体积单位的累加”,所以没有很好地建立起“长方体体积”的概念。
如果在这个过程中,教师重视学生操作的过程,让学生体会到用棱长为1厘米的小正方体摆长方体,摆一排的数量和长方体的长一样,也就是长是几就摆几个;摆一层的数量和长方体的长×宽(也就是底面积)一样,也就是宽是几就摆几排;摆完整个长方体的数量和长方体的长×宽×高一样,也就是高是几就摆几层。从而得出,长方体的体积就是摆的总个数,而这个总个数,不用一个一个地去数了,可以用长×宽×高这个简便方法计算出来。也就是一共用了几个小正方体,得到的长方体的体积就是几个这样的体积单位。这就是“基于体积单位理解图形体积”“理解体积是体积单位的累加”。
有了这些基础,学生再理解从长方体、正方体、圆柱体的体积公式向其他形体进行拓展时,就会知道无论底面是什么形状,所说的“底面积”就是一层的“单位数量”,再乘高就是总的单位数量,就是体积。这就很容易拓展得出“所有直柱体的体积都可以用V=Sh计算”的结论。这时,学生对直柱体体积的理解就不只是记住了体积计算公式那么简单,还建立起了直柱体体积的概念。
以上这三道拓展题的相通之处在于对“度量单位”的理解,应该通过这样的拓展题,让学生在理解1°角、1平方厘米、1立方厘米的基础上明白“以15°为一个单位可以画出15°的倍数的角”“以4平方厘米为一个单位可以度量出一个图形有多少个这样的单位”“1立方厘米体积的形状不仅限于棱长是1厘米的正方体,用不规则形状的体积单位也可以去度量体积”。这样的拓展题就不只是题的拓展,而是思维的拓展、理念的拓展。
参考文献:
[1]刘坚,孔企平,张丹.义务教育教科书数学(2014年版)[M].北京:北京师范大学出版社,2022.
(责任编辑:杨强)

