依标据本，素养立意

徐娟 任炯

摘要：2022年成都市中考数学压轴题是一道有效考查数学核心素养的好题目，并通过“尝试初探—深入探究—拓展延伸”的深度探究模式有效考查了学生的数学探究能力．从命题立意、解法探究、问题变式等角度对该题作了一番探究．

关键词：中考数学压轴题；依标据本；数学核心素养

2022年成都市中考数学试题以《义务教育数学课程标准（2022版）》［1］和现行教材为基本依据，全面、系统地考查了数学知识技能、思想方法和思维品质，重视不同考生思维层次水平的区分．特别是压轴题，以矩形为基架构题，展示“图随点动”的过程中的变与不变，试题构图简洁，成题自然，问题设置由浅入深，由特殊到一般，循序渐进，层次分明，形式多样，韵味十足．这道压轴题通过“尝试初探—深入探究—拓展延伸”的深度探究模式有效考查了学生的数学探究能力．

1试题呈现

如图1，在矩形ABCD中，AD＝nAB（n＞1），点E是AD边上一动点（点E不与A，D重合），连接BE，以BE为边在直线BE的右侧作矩形EBFG，使得矩形EBFG∽矩形ABCD，EG交直线CD于点H．

【尝试初探】（1） 在点E的运动过程中，△ABE与△DEH始终保持相似关系，请说明理由．

【深入探究】（2） 若n＝2，随着E点位置的变化，H点的位置随之发生变化，当H是线段CD中点时，求tan∠ABE的值．

【拓展延伸】（3） 连接BH，FH，当△BFH是以FH为腰的等腰三角形时，求tan∠ABE的值（用含n的代数式表示）．

2命题立意分析

2.1以数学知识与技能立意

试题将矩形、直角三角形、相似三角形、勾股定理、等腰三角形、图形运动变换等融为一体，涉及初中平面几何的多个核心知识点．考查了学生计算、推理、迁移能力以及相关知识的综合运用．

2.2以数学思想方法立意

试题全方位考查了初中数学思想方法．该题不仅考查了学生自主构图的能力，还全面地考查了分类讨论、数形结合、联想类比、方程思想、由特殊到一般等数学思想方法的灵活运用．试题自然合理、严谨理性，有利于甄别学生的思维层次，具有选拔的功能．

2.3以数学树人与育人立意

北师大版初中数学教材以“问题情境—建立模型—解释、应用和拓展”的模式展开，教材的设置有助于培养学生发现问题、提出问题、分析问题、解决问题的能力．本题作为压轴题以“尝试初探—深入探究—拓展延伸”的台阶式模式完全符合教材的逻辑顺序，这种低起点切入、层层递进的呈现方式，符合学习情境，能提升学生解题的兴趣与信心，增强学生知识运用的能力，实现数学树人与育人目标．

3解法探究

本题第1问是一线三垂直模型，相对简单，第2问以第1问为思维起点，相对比较容易，不做探究．下面主要研究第3问，此类探究型问题的解题策略主要考查学生“几何直观→几何本质→几何推理”三个能力维度．

3.1会自主构图，获几何直观

自主构图是考查學生的初步抽象能力、几何直观和空间想象能力．由题意，不难判断此问需要分类讨论，分别以FH=FB，HF=HB展开讨论，借助题目中给出的图1，题干中“点E是AD边上一动点”与“EG交直线CD于点H”说明H点可能在线段CD上，也可能在线段DC的延长线上．点E从A运动到D的过程中H点的变化是在DC线段上→DC延长线上→DC线段上．

3.2探运动规律，究几何本质

在运动过程中始终有△ABE∽△DEH，△ABE∽△CBF， 抓住在运动的过程中不变的量，保持解题思维的一致性，由特殊到一般，最后迎刃而解．

3.3会综合运算，善几何推理

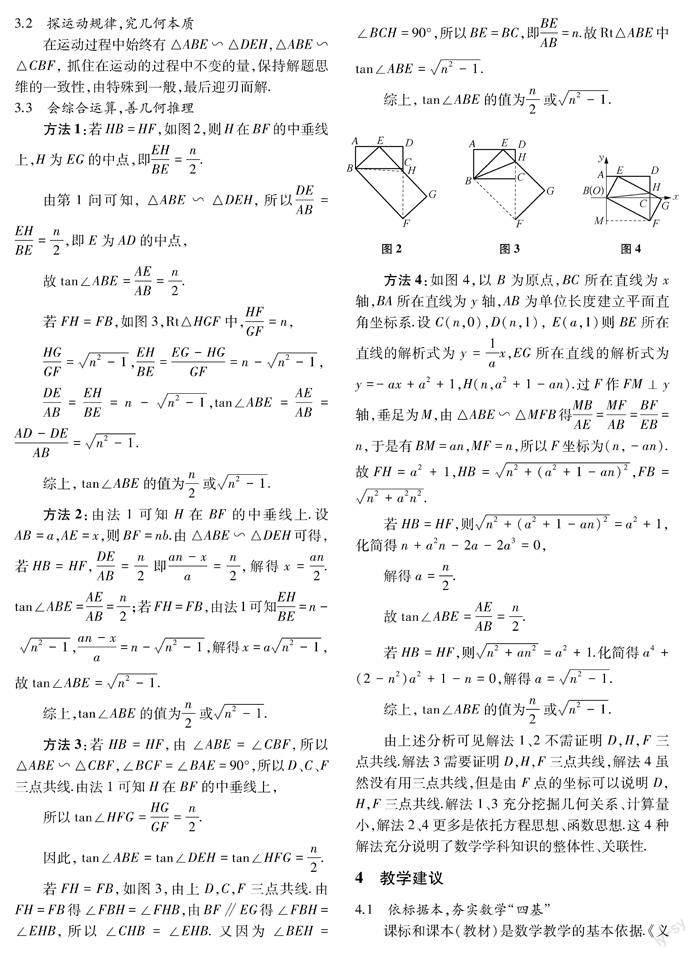
方法1：若HB=HF，如图2，则H在BF的中垂线上，H为EG的中点，即EHBE=n2．

由第1问可知，△ABE∽△DEH，所以DEAB=EHBE=n2，即E为AD的中点，

故tan∠ABE=AEAB=n2．

若FH=FB，如图3，Rt△HGF中，HFGF=n，

HGGF=n2－1，EHBE=EG－HGGF=n－n2－1，

DEAB=EHBE=n－n2－1，tan∠ABE=AEAB=AD－DEAB=n2－1．

综上，tan∠ABE的值为n2或n2－1．

方法2：由法1可知H在BF的中垂线上．设AB=a，AE=x，则BF=nb．由△ABE∽△DEH可得，若HB=HF，DEAB=n2即an－xa=n2，解得x=an2．tan∠ABE=AEAB=n2；若FH=FB，由法1可知EHBE=n－n2－1，an－xa=n－n2－1，解得x=an2－1，故tan∠ABE=n2－1．

综上，tan∠ABE的值为n2或n2－1．

方法3：若HB=HF，由∠ABE=∠CBF，所以△ABE∽△CBF，∠BCF=∠BAE=90°，所以D、C、F三点共线．由法1可知H在BF的中垂线上，

所以tan∠HFG=HGGF=n2．

因此，tan∠ABE=tan∠DEH=tan∠HFG=n2．

若FH=FB，如图3，由上D，C，F三点共线．由FH=FB得∠FBH=∠FHB，由BF∥EG得∠FBH=∠EHB，所以∠CHB=∠EHB．又因为∠BEH=∠BCH=90°，所以BE=BC，即BEAB=n．故Rt△ABE中tan∠ABE=n2－1．

综上，tan∠ABE的值为n2或n2－1．

方法4：如图4，以B为原点，BC所在直线为x轴，BA所在直线为y轴，AB为单位长度建立平面直角坐标系．设C（n，0），D（n，1）， E（a，1）则BE所在直线的解析式为y=1ax，EG所在直线的解析式为y=－ax+a2+1，H（n，a2+1－an）．过F作FM⊥y轴，垂足为M，由△ABE∽△MFB得MBAE=MFAB=BFEB=n，于是有BM=an，MF=n，所以F坐标为（n，-an）．故FH=a2+1，HB=n2+（a2+1－an）2，FB=n2+a2n2．

若HB=HF，则n2+（a2+1－an）2=a2+1，化简得n+a2n－2a－2a3=0，

解得a=n2．

故tan∠ABE=AEAB=n2．

若HB=HF，则n2+an2=a2+1．化简得a4+（2－n2）a2+1－n=0，解得a=n2－1．

综上，tan∠ABE的值为n2或n2－1．

由上述分析可见解法1、2不需证明D，H，F三点共线．解法3需要证明D，H，F三点共线，解法4虽然没有用三点共线，但是由F点的坐标可以说明D，H，F三点共线．解法1、3充分挖掘几何关系、计算量小，解法2、4更多是依托方程思想、函数思想．这4种解法充分说明了数学学科知识的整体性、关联性．

4教学建议

4.1依标据本，夯实数学“四基”

课标和课本（教材）是数学教学的基本依据．《义务教育数学课程标准（2022年版）》指出：“到了初中阶段，主要侧重学生对图形概念的理解，以及对基于概念的图形性质、关系、变化规律的理解．”从上述几种解法可以看出，试题完全符合课程标准理念．因此在教学中，应当以课标为准，以教材为本．教材是宏观、静置、储存式的知识状态，教师在教学中应该将这样的知识状态通过加工转化为微观、流动、提取式的知识，能让学生主动理解、吸收．章建跃先生关于数学教学的“三个理解”的内涵：特别强调“内容所反映的数学思想方法”的理解，决定了教学所能达到的水平和效果．所以在初中数学教学过程中，教师在充分理解知识的来龙去脉同时，必须有意识地坚持“数学思想的渗透”，引导学生在数学学习过程，体会知识点或某一个试题（问题）背后所隐含的数学思想方法，帮助学生夯实“四基”，实现数学课程价值．

4.2把握体系，提升数学“四能”

初中“图形与几何”部分着手培养学生的“直观→抽象”能力，几何部分考查学生数学论证的逻辑推理能力．在教学中教师应该建构完整的知识体系，分析每一课的教学内容在整个课程的地位以及前后联系．适当类比归纳、巧用灵活变式引导学生主动发现问题、提出问题、分析问题、解决问题．以此题为例，原型是北师大教材八年级下综合复习题20题．原题条件是：正方形ABCD中，E在线段AB上，F在线段AD延长线上，BE=DF，问是否存在两个全等的三角形？其中一个三角形能够通过旋转另外一个三角形而得到吗？如果在教学中，能将图形的变化、全等、相似、平面直角坐标系、方程、三角函数等知识整合在一起，经过如下2个灵活变式、类比教学，引导学生归纳提炼模型，有助于发展学生的几何素养．

变式1：正方形ABCD中，E在线段AB上，将△BCE绕点C顺时针旋转90°（或作等腰直角△ECF），则A，D，F三点共线吗？

变式2：长方形ABCD中，E在线段AB上，作CE⊥CF，且CECF=CBCD，则A，D，F三点共线吗？

模型提炼：如图6，OA=OB，C为AB上一点，OC=OD，且∠AOB=∠COD，则有如下结论：① △OAC≌△OBD，② 点D的运动轨迹为一条直线；③ O，C，B，D四点共圆．再将C推广到在直线AB上运动，上述结论依然成立．如图7、图8，C为直线AB上一点，OAOB=OCOD，

∠AOB=∠COD，則有如下结论：① △OAC∽△OBD，② 点D的运动轨迹为一条直线；③ O，C，B，D四点共圆．

深挖教材：通过变换条件与结论有助于帮助学生抓住几何本质，以教材和变式1作为低起点进行变式2，将全等三角形推广为相似三角形的情况，一方面体现从特殊到一般的数学思想方法，另一方面符合学生的认知规律．提炼基本图形有助于学生理解图形的内涵，形成解题的通法进行拓展应用．应用1是对模型的拓展运用，应用2是将C为线上的一点推广为平面内一点，进行进一步的推广．

应用1如图9，正方形ABCD的边长为2，对角线AC，BD相交于点O．将△OBC绕点B逆时针旋转得到△O′BC′，当O′，C′，D′三点共线时，O′A的长为．

应用2如图10，已知等边三角形ABC的边长为5，点D为平面内一动点，且DA＝1，将点D绕点C按逆时针方向转转60°，得到点E，连接AE，则AE的最大值是．

全面把握知识体系，整合“图形的性质”“图形的变化”“图形与坐标”三个主题的教学．在教学中，适当的变式训练不仅能激发学生的兴趣，还能为学生的思维搭建台阶，帮助学生建构完整的知识体系．变式训练是提升学生思维灵活性的重要手段之一，亦是发展学生数学核心素养的基本手段．这种采用低切入、缓坡度、成系统的教学策略能够全面提升学生的数学“四能”．

4.3训练思维，发展数学核心素养

初中“图形与几何”的教学既是立德树人的好素材，也是训练几何思维的好素材、发展数学核心素养．数学思维训练是培养数学核心素养的重要策略，数学思维的训练包括对数学语言、数学思维方法以及思维品质的训练．“图形与几何”的学习可以通过通常所说的“看图”“想图”“构图（即画图）”“探图（即探究图形性质）”“用图（即应用图形的性质）”等几何思维方法来发展数学核心素养．关于“看图”，起始阶段通过信息技术的演示或者实物的操作，让学生感受基本特征，知道基本性质，感悟图形有规律变化产生的美．关于“想图”“构图”，要注重学生构图能力的培养，探究用几何知识表达物体简单的运动规律，有助于培养学生几何直观．关于“探图”，在图形的性质教学方面，探究思路和方法应具有层次性，让学生感悟几何体系的基本框架，会用数学的思维思考现实世界．关于“用图”，通过提炼基本图形、总结推广模型形成解决问题的思路，发展模型观念，有助于发展学生理解几何知识的本质．学生在经历上述思维过程后，提升思维广阔性、灵活性、深刻性、批判性、独创性．从而发展学生的数学核心素养．

参考文献：

［1］ 中华人民共和国教育部.义务教育数学课程标准（2022年版）［S］.北京：北京师范大学出版社，2022.

［2］ 章建跃.章建跃数学教育随想录［M］.杭州：浙江教育出版社，2017：6.

［3］ 徐娟.2020年成都市中考第27题阅卷分析及启示［J］.中学数学，2021（4）：49-50.

［4］ 张彬政.学科核心素养理念下提升高中学生数学思维品质的教学策略［J］.数学教学通讯，2022（4）：38-39.

［5］ 赵思林.数学核心素养的培养策略［J］.数学通报，2019，58（5）：28-32.