从一道数学试题的命制过程分析数学核心素养的考查方法

王志刚+阮飞

[摘 要] 数学评价必将从“能力立意”转变为“素养立意”. 怎样在试题命制过程中渗透数学核心素养，怎样用核心素养的观点分析评价试题是现代教学需要着重思考的问题.

[关键词] 数学核心素养；数学评价；试题命制；能力立意；素养立意

引言

时代变化了，教育的要求变了，呼唤核心素养的出现. “核心素养是新课标的来源，也是确保课程改革万变不离其宗的‘DNA，考试评价的方式和内容正在悄然地改变，围绕发展学生的核心素养的教育评价体系正在逐步形成，未来三到五年的数学考试评价必将从“能力立意”转变为“素养立意”.

正文

数学核心素养是具有数学基本特征的、适应个人终身发展和社会发展需要的人的关键能力与思维品质. 数学核心素养是数学课程目标的集中体现，是学生在数学学习的过程中逐步形成的.数学核心素养包括三个方面，六个关键词：用数学的眼光观察世界，发展数学抽象、直观想象素养；用数学的思维分析世界，发展逻辑推理、数学运算素养；用数学的语言表达世界，发展数学建模、数据分析素养. 核心素养很重要，这一点估计没人会反对. 但问题是，很多老师不知道如何去操作落实，这是摆在我们老师面前的现实问题. 林崇德教授给出这样的指导意见：“核心素养具有可教、可学的外显部分，同时也存在无声、无形但可感、可知的内隐部分. 前者能够在特定的情境下通过一定的方式表現出来，因此能够有效地对其进行定量的测评……”基于此，笔者在试题的命制过程中进行了一些尝试.

一、题目名称

导数的几何意义和函数不等式证明问题.

二、题目分析

1. 试题的命制思路分析

此题是基于数学情境命制的试题，试题素材来源于教材中导数的几何意义，背景是函数f（x）=ex在x=0处和u（x）=lnx在x=1处的泰勒展开式.

第（Ⅰ）问直接考查导数的几何意义.由于函数f（x）=ex和u（x）=lnx互为反函数，且f（x）在（0，1）处的切线m和u（x）在（1，0）处的切线n平行，把n和u（x）向左平移2个单位就得到m和g（x）=ln（x+2）. 因此引入参数a，构造新函数g（x）=ln（x+a）.控制参数a的取值范围可保证f（x）>g（x），于是抽象出第（Ⅱ）问. 通过几何画板演示发现参数a有最大值，最大值是多少呢？（笔者注：我们猜想这个最大值与欧米伽常数有关）通过探索发现高中知识很难解决这个问题，于是给出相关数据，改为求参数a最大值的近似值.

2. 考查目标分析

本题在较复杂的数学情境下考查函数图像在某一点处的切线与函数导数的关系，即导数的几何意义，考查导数公式和导数运算法则、函数最小值、导数、函数零点的概念，考查考生灵活运用导数工具借助已知数据去分析问题、解决问题的能力，综合考查考生的逻辑推理能力、运算求解能力、推理论证能力以及转化与化归、数形结合的思想.

3. 试题设问及解答过程中涉及的数学核心素养分析

（1）逻辑推理和数学运算素养

逻辑推理是指从一些事实和命题出发，依据逻辑规则推出一个命题的思维过程，主要包括两类：一类是从特殊到一般的推理，推理形式主要有归纳、类比；一类是从一般到特殊的推理，推理形式主要有演绎.数学运算是指在明晰运算对象的基础上，依据运算法则解决数学问题的过程，主要包括：理解运算对象，掌握运算法则，探究运算方向，选择运算方法，设计运算程序，求得运算结果等.

第（Ⅰ）问的设计面向全体考生，要解决这个问题，考生要具备毕业水平的逻辑推理素养：在对曲线切线的概念充分理解的基础上，由分析法知，需要求切点坐标和切线的斜率；还要具备毕业水平的数学运算素养：准确应用导数公式和求导法则进行导数运算就可以求切点坐标和切线的斜率，再写出切线的点斜式方程.

（2）数学建模和直观想象素养

数学建模是对现实问题进行数学抽象，用数学语言表达问题、用数学知识与方法构建模型解决问题的过程，主要包括：在实际情境中从数学的视角发现问题、提出问题，分析问题、构建模型，求解结论，验证结果并改进模型，最终解决实际问题.笔者认为也应包括构造新的数学模型解决数学问题的过程. 直观想象是指借助几何直观和空间想象感知事物的形态与变化，利用图形理解和解决数学问题的过程，主要包括：借助空间认识事物的位置关系、形态变化与运动规律；利用图形描述、分析数学问题；建立形与数的联系；构建数学问题的直观模型，探索解决问题的思路.

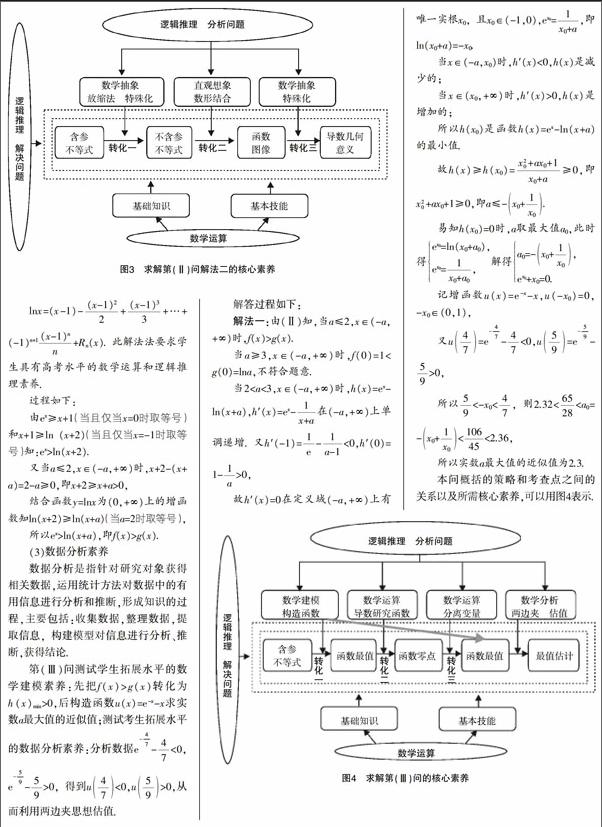
解答（Ⅱ）问时要把f（x）>g（x）转化为h（x）min>0，能测试学生高考水平的数学建模素养和数学计算和逻辑推理素养：在求解过程在发现不易判断h′（x）=ex-的正负号，得不到h（x）的单调性，但借助图形可以发现当a≤2，x∈（-a，+∞）时ex-ln（x+a）≥ex-ln（x+2），借助放缩法把问题转化为证明ex-ln（x+2）>0. 这就考查了学生的直观想象、数学运算和逻辑推理的素养.

下同原题第（Ⅲ）问的解法.

从以上分析可以看出，在解答本题时起决定作用的是逻辑推理、数学建模、直观想象、数学运算和数据分析五大核心素养. 在将新问题转化为旧问题，复杂问题转化为简单问题的过程中，数学核心素养起着重要的作用，而知识和技能只有在具体求解时才能发挥作用.

数学核心素养虽划分为三个方面，六个关键词，但它们既有独立性，又相互交融，形成一个有机整体. 用数学的眼光观察世界，即人从外界输入信息；用数学的思维分析世界，即人处理信息；用数学的语言表达世界，即人输出信息.