普通高中促进学生“数学基本活动经验”积累的实验和思考

陆剑钢

[摘 要] 为探索普通高中基础薄弱的学生数学学业发展的途径，开展教学微实验研究.研究表明帮助学生获得以归纳活动经验和演绎活动经验为主体的数学基本活动经验，能使学生掌握归纳和演绎的思维方法，能激发学生数学学习的源动力，帮助其进入学数学、用数学的良性循环，是促进学生学业发展的有效途径.

[关键词] 基本数学活动；数学基本活动经验

实验的背景和意义

1. 数学基本活动经验

史宁中先生在2015年全国优秀教师培训技能提升研修班上题为“为什么要学习数学——兼论数学核心素养”的讲座中提到了数学“四基”，即数学基础知识、数学基本技能、数学基本思想和数学基本活动经验.实际上，史先生提出数学“四基”可以追溯到2006年，当时便引起了张奠宙先生、王新民先生等有识之士的共鸣.

王新民先生认为：数学活动经验是指学习者在参与数学活动的过程中所形成的感性知识、情绪体验和应用意识.而最基本、最主要的数学活动是以逻辑为特征的演绎论证活动和以经验为特征的归纳发现活动，其他的数学活动都是围绕这两种活动而展开的.因此可以把归纳活动经验和演绎活动经验称为数学基本活动经验.

2. 实验的背景

笔者任教的高一班级数学中考平均分为95分，学生的数学素养和数学学习能力相对较为薄弱，以下一组通过考试测得的数据可以管窥一二.

（1）求函数y=Asin（ωx+φ）图像上相邻的最高点（x1，y1）和最低点（x2，y2）之间的距离d，83.7%的学生认为两点间的距离d=x1-x2，说明学生对数学概念的认识不清晰.

（2）证明函数y=的单调性，93.0%的学生无法完成作差变形，说明学生欠缺数学运算的能力.

显然，这些学生的“双基”是薄弱的.调查显示他们在初三数学学习的过程中，几乎不主动参与归纳活动和演绎活动，且在活动中很少自主收获成果，数学基本活动经验非常缺乏.在此学情下，若继续墨守成规，只会使得情况更糟.

3. 实验的意义

史宁中先生认为“数学基本活动经验”与数学“双基”和“数学基本思想”是相互依存的，共同构成了学生的数学认知结构.数学基本活动经验可以巩固学生的“双基”，可以直接影响学生数学思想方法的形成，对数学教学有着潜移默化的作用.本实验旨在帮助教师革新教学模式，探索基础薄弱的学生数学学习新的助力点，研究帮助学生获得数学基本活动经验的模式，帮助学生体悟数学方法和思维在现实问题解决过程中的意义和作用，帮助学生认识数学、理解数学和使用数学，以此促进学生的学业发展.

实验假设

参与基本数学活动的学生，数学基本活动经验，即归纳和演绎活动经验会得到提高，数学思维的宽度、力度会有所发展，养成良好的数学修养，学业发展能优于其他学生.同时，他们能更好地体会数学的应用价值，具备一定的数学实践能力，为终身发展奠定基础.

实验方法

1. 实验设计

实验采用等组前后测的设计，前测为中考数学成绩，实验时间为一个学期. 自变量为课外辅导方法，有两个取值，分别是开展基本数学活动和无措施. 后测（因变量）为高一第一学期期末数学考试成绩.

对实验组组织基于第二课堂的，有步骤、有计划、连贯性的基本数学活动，帮助学生在活动中解决问题，积累数学基本活动经验，促使学生思考数学知识和数学思维对个人生涯发展的影响.控制组不进行任何课外辅导.

2. 被试

采用系统抽样构成样本，将班级学生按中考数学成绩，用Excel从高到低排序，同分数的学生因excel自動排序故名次均不同，选取第5、10、15、20、25、30、35、40名的8位学生组成实验组，将第4、9、14、19、24、29、34、39名的8位学生组成控制组.

3. 效度

被试均为高一学生，年龄、能力、智商无显著差异. 实验环境为自然学习环境，被试不知道本身正处于实验阶段.系统抽样可减少统计误差，即各组平均分的差异不会对实验结果产生干扰.数学教学均由笔者担任，教学时间和方法、作业量均统一，努力控制无关变量.

实验目的

通过观察被试学业成绩的变化，对比分析数学基本活动经验对数学学习的影响，探索适合普通高中基础薄弱的学生的学业发展模式，并由此调整教师的教学思路和方法，形成学生想学能学、教师轻负的师生双赢的教学模式.

实施阶段

1. 通过概率实验帮助学生获得数学基本活动经验

组织实验组分析和解决三扇门问题、蒲丰投针实验等. 在教师的引导下，通过概率实验分析数据，归纳规律，寻找破题路径或发现问题，尝试解释原因，并形成研究报告，着重让学生在活动中主动获得归纳和演绎的经验.

例1（三扇门问题）：竞猜者会看见三扇关闭的门，有且仅有一扇门后有礼物，选对门就可以赢得礼物. 当竞猜者选定一扇门后，裁判不打开门，而是打开剩下两扇门中没有礼物的一扇门，让竞猜者看到. 这时，裁判会给竞猜者一次重新选择的机会，竞猜者应该坚持原来的选择还是要改变原来的决定选择另一扇关上的门呢？（注：裁判知道礼物放在哪扇门后）

由此学生能直观得出结论“应该改变原来的决定选择另一扇关上的门”，并大胆猜测其概率为，再演绎问题本质，给出解释：事件“改变原来的决定并选中礼物”相当于“最初从三扇门中选择一扇没有礼物的门”.

在类似的实验过程中，学生能清晰地体会到归纳和演绎经验所发挥的作用，能认识到归纳为演绎提供线索，而演绎为归纳正名.

2. 通过试题研究帮助学生获得数学基本活动经验

组织实验组从定性和定量的角度开展试题研究活动.通过运用直觉、猜想、悖向探索、特例验算等定性分析的思维形式，给出问题研究可能的方向，再通过演绎推理，给出问题的定量分析，力争让学生在活动中主动获得归纳和演绎的经验.

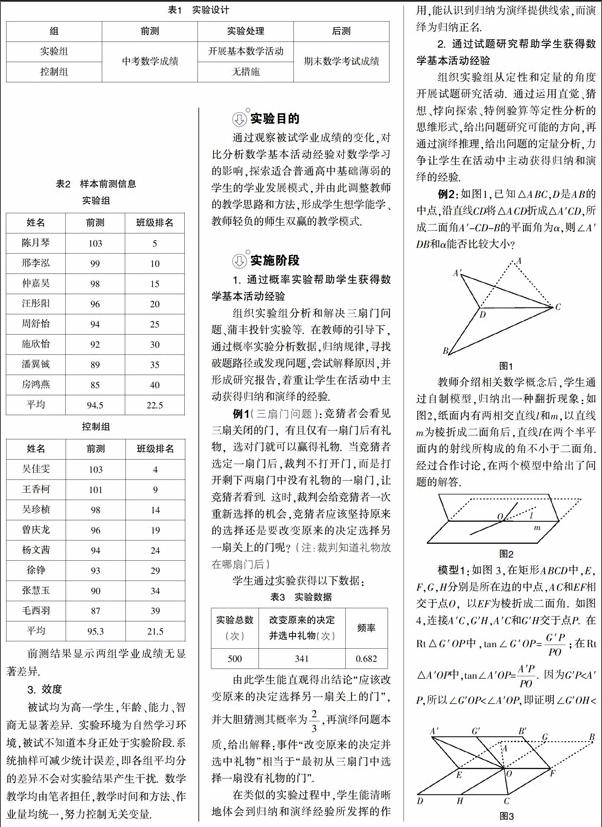
例2：如图1，已知△ABC，D是AB的中点，沿直线CD将△ACD折成△A′CD，所成二面角A′-CD-B的平面角为α，则∠A′DB和α能否比较大小？

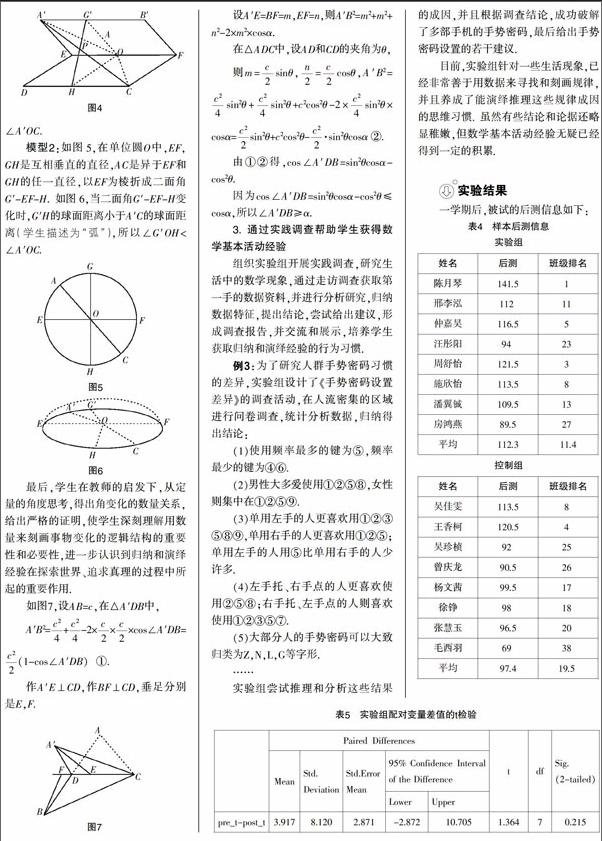
教师介绍相关数学概念后，学生通过自制模型，归纳出一种翻折现象：如图2，纸面内有两相交直线l和m，以直线m为棱折成二面角后，直线l在两个半平面内的射线所构成的角不小于二面角.经过合作讨论，在两个模型中给出了问题的解答.

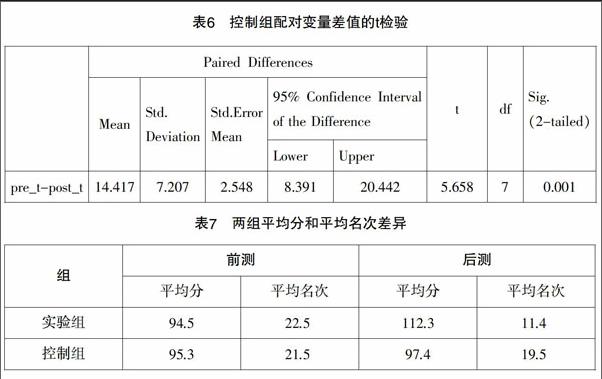
模型1：如图3，在矩形ABCD中，E，F，G，H分别是所在边的中点，AC和EF相交于点O，以EF为棱折成二面角. 如图4，连接A′C，G′H，A′C和G′H交于点P. 在Rt△G′OP中，tan∠G′OP=；在Rt△A′OP中，tan∠A′OP=. 因为G′P

模型2：如图5，在单位圆O中，EF，GH是互相垂直的直径，AC是异于EF和GH的任一直径，以EF为棱折成二面角G′-EF-H. 如图6，当二面角G′-EF-H变化时，G′H的球面距离小于A′C的球面距离（学生描述为“弧”），所以∠G′OH<∠A′OC.

最后，学生在教师的启发下，从定量的角度思考，得出角变化的数量关系，给出严格的证明，使学生深刻理解用数量来刻画事物变化的逻辑结构的重要性和必要性，进一步认识到归纳和演绎经验在探索世界、追求真理的过程中所起的重要作用.

3. 通过实践调查帮助学生获得数学基本活动经验

组织实验组开展实践调查，研究生活中的数学现象，通过走访调查获取第一手的数据资料，并进行分析研究，归纳数据特征，提出结论，尝试给出建议，形成调查报告，并交流和展示，培养学生获取归纳和演绎经验的行为习惯.

例3：为了研究人群手势密码习惯的差异，实验组设计了《手势密码设置差异》的调查活动，在人流密集的区域进行问卷调查，统计分析数据，归纳得出结论：

（1）使用频率最多的键为⑤，频率最少的键为④⑥.

（2）男性大多爱使用①②⑤⑧，女性则集中在①②⑤⑨.

（3）单用左手的人更喜欢用①②③⑤⑧⑨，单用右手的人更喜欢用①②⑤；单用左手的人用⑤比单用右手的人少许多.

（4）左手托、右手点的人更喜欢使用②⑤⑧；右手托、左手点的人则喜欢使用①②③⑤⑦.

（5）大部分人的手势密码可以大致归类为Z，N，L，G等字形.

……

实验组尝试推理和分析这些结果的成因，并且根据调查结论，成功破解了多部手机的手势密码，最后给出手势密码设置的若干建议.

目前，实验组针对一些生活现象，已经非常善于用数据来寻找和刻画规律，并且养成了能演绎推理这些规律成因的思维习惯. 虽然有些结论和论据还略显稚嫩，但数学基本活动经验无疑已经得到一定的积累.

实验结果

一学期后，被试的后测信息如下：

将前测和后测均换算为百分制后，对两组样本进行配对样本t检验分析，所得结果见表5和表6.

表5中的pre_t是前测，post_t是后测，可以看到，Mean均值之间的差值为3.917；Std.Deviation差值的标准差为8.120；Std.Error Mean差值的标准误为2.871；95% Confidence Interval of the Difference均值差值的95%置信区间为（-2.872，10.705），包含0；t检验的t值为1.364，自由度df为7，双尾t检验显著性概率p=0.215>0.05. 可以认为开展基本数学活动后，学生的前测和后测没有显著差异.

表6显示95% Confidence Interval of the Difference均值差值的95%置信区间为（8.391，20.442），不包含0；双尾t检验显著性概率p=0.001<0.05. 可以认为无措施对学生的学业发展也有显著的影响. 但因为Mean均值之间的差值为14.417>0，说明后测显著低于前测，所以这种影响是消极的.

从实验结果看，实验组前后测没有显著差异；控制组前后测差异明显，且后测显著低于前测. 因此从维持学生成绩的角度看，积累数学基本活动经验优于无措施.

实验结果分析和讨论

为什么实验组前后测没有显著差异，成绩仅仅维持原来水平呢？这是由初、高中数学学科固有的差异造成的，在高中考试中维持中考分数的水平是很困难的. 如中考考115分的学生要维持原有水平，在高中就要考到143.75分，这显然是有一定难度的.

从表7看到，实验组后测的平均分明显高于控制组，说明整体存在較大的进步. （相对）优等生依然保持名列前茅，没有出现均分回归现象，其余学生进步明显.

经观察和试验，实验组的学生相对控制组的学生表现出了以下差异：

（1）对数学学习表现出兴趣，有主动获取数学知识的意愿.

（2）课堂学习中更注重知识产生的过程.

（3）在研究问题时更重视归纳和演绎思想的运用.

（4）能用归纳和演绎思想来解释现实问题.

实验结果表明：

（1）数学基本活动经验的积累对普通高中基础薄弱的学生学业发展有很大的促进作用. 一方面，能帮助学生掌握归纳和演绎的思维方法，能促使学生的数学思维变得更为有序和合理，能使学生理解数学基础知识，提高数学基本技能，提高解决数学问题和实际问题的能力. 另一方面，能帮助学生形成用数学探究现象的科学态度，激发学生数学学习的源动力，促使其进入“学数学——用数学——学数学”的良性循环，为今后持续的学业发展乃至生涯发展奠定基础.

（2）基于第二课堂的小课题研究有利于帮助学生获得数学基本活动经验. 本实验设计包含概率实验、试题研究和实践调查三种方式，均采取第二课堂下的小团体自主选择开展小课题研究的形式，这有利于激发学生的主观能动性，有利于学生发挥自身的能力优势、环境优势. 有着问题导向的小课题合作研究，能让学生在问题情境中亲历归纳和演绎经验的产生及发展的过程，获得解决问题的成功体验，因而有助于学生自主地内化和提升数学基本活动经验，能促使学生主动地从现实的“经历”走向抽象概括的“经验”.

对实验的思考

1. 要重视数学基本活动经验

随着社会经济的发展和我国教育改革的深入，国家对人才的现实需求和学生个体发展的客观需要都要求教师要将眼光放得更远，要形成正确的教学价值观，要重视数学基本活动经验的积累在学生生涯发展中的作用.无论是第一课堂还是第二课堂，教师都要创造帮助学生获得数学基本活动经验的机会.尤其是基础薄弱的学生，由于数学基础和学习能力的限制，一般地，练习讲评会占据着更多的课堂教学时间，针对这种情况，教师更应在课堂教学中引导学生参与归纳和演绎活动，帮助学生获得数学基本活动经验.

2. 要研究基本数学活动的有效性

基本数学活动是学生生成、拓展和交流数学基本活动经验的过程，同时也是学生获得数学基础知识、基本技能与基本思想的过程.为了帮助学生获得有价值的数学基本活动经验，教师要研究基本数学活动的有效性，避免出现活动热闹、收效甚微的结果.基本数学活动需要精心设计的问题情境，需要知识产生或运用的过程，需要高效畅通的交流平台，以激活学生的归纳和演绎思维，使学生掌握思维的策略和方法，使自身的思维更具批判性和深刻性.

同时，教师还应引导学生深入思考基本数学活动的意义，完成经验的创造、领悟、反思、内化、检验和重新创造.帮助学生形成自主获得数学基本活动经验的意识和能力，助力学生的可持续发展.