双船联合举升多体协同作业系统横摇稳性评估

李德江,邓兴旗,赵树杰,孟 珣

(1.中国海洋大学工程学院,山东 青岛 266100; 2.烟台中集来福士海洋工程有限公司,山东 烟台 264035)

海洋平台上部组块的安装/拆除作业是海洋资源开发全生命周期的重要环节,其中海上吊装和海上浮托作业技术被广泛应用于上部组块施工过程。相比于吊装,浮托作业具有举升容量大、成本低的优势,是万吨级上部组块一体化安装/拆除作业的首选方案[1]。为了满足不同作业需求,多类浮托技术应运而生,根据涉及的驳船类型可分为3类:单驳船浮托[2]、双体船浮托[3]和双驳船浮托[4]。

单驳船浮托技术是最早应用、也是最常用的海洋平台浮托施工作业技术,但需要基础支撑结构有足够大的顶部开口以允许驳船驶入,因此会受到既有平台结构形式的限制。与单驳船浮托技术相比,双体船浮托作业具有更大的举升能力,其船体在船首或船尾设置U形开口槽,船体能从平台结构两侧进入。最具代表性双体作业船为Allseas的“Pioneering Spirit”[5],该船于2016年8月完成了北海海域Yme-MOPU导管架基础的拆除作业[3]。相比于前两者,双驳船浮托具有更高的灵活性,每艘作业船舶可在非一体化浮托作业期开展运输、吊装等其他独立作业,从而提高船舶利用率。当两艘独立驳船协同作业时,双船与上部组块间以有运动补偿的连接方式组成一个复杂的多体系统,双船运动的不同步性使其横摇稳性与单驳船浮托技术和双体船浮托技术明显不同。海上浮托作业对海洋环境条件敏感[6-8],波高和波浪周期的变化会使上部组块和船舶的运动变得显著[9],从而增加失稳风险。为了减少操作中横摇失稳风险,大多数单驳船与双体船浮托作业工程中[4,10],驳船和上部组块之间都采用刚性连接构件连接以限制其相对运动。虽然刚性连接可以保证系统的横摇稳性,但需要对上部组块进行加强设计,以满足加强件和结构核心受力区域在安装时的强度要求。Koo等[11-12]对Spar平台的浮托作业进行了数值分析和试验分析,发现上部组块承受了较大的波浪动力荷载,从而影响了结构的强度设计。Dessi等[13]使用刚性模型和弹性连接模型对上部组块的响应进行了试验分析,发现结构间的弹性连接会导致系统产生较大的横摇运动。近年来,有学者开始对典型工况下双船的运动特性进行分析[14-19],但这些研究多基于举升系统和组块间的刚性连接假定。

对于举升系统与上部组块间采用柔性连接形式的双驳船浮托作业多体系统,Zhao等[20-21]指出该类型系统横摇耦合响应对举升作业状态具有重要影响。本文采用数值模拟和模型试验结合的方式,研究柔性连接形式的双船联合举升多体协同作业系统在不确定海况中的多体横摇稳性问题,并给出该系统上部组块横摇稳定性极限准则的快速分析方法与预测手段。

1 双船联合举升多体协同作业系统及作业过程

超大型海上油田设施拆解作业是一项涉及多领域的系统性工程,技术含量高、作业风险大,需要充分考虑拆解作业的安全和环保等要素要求。本文研究的多功能起重船是全球首制的超大型海上油气设施一体化拆解和安装、海上风电装置安装等多功能装备,主要由2艘起重船组成,配备DP3动力定位系统,可选择配置带运动补偿的举升臂系统,总起重能力最高可达3万t。双船联合进行一体化拆解和安装的作业模式具有操作灵活、高效的特点,但其可调的举升系统外沿臂以及举升头和甲板支撑配备运动补偿使得作业过程中上部组块和船体多体耦合运动机制复杂,明显不同于传统浮托作业中采用刚性连接假定的单刚体稳性概念。针对待拆解模块不同尺度特征,举升点之间距离的选择对横摇稳性影响为本文关注重点。

1.1 双船联合举升多体协同作业系统

双船联合举升系统示意图及其关键结构装备如图1所示,在整体坐标系中,x0轴沿船舶纵荡方向,y0轴沿船舶横荡方向,z0轴沿船舶垂荡方向。每艘作业船均配备先进的动力定位系统,可限制船体在水平面内的漂移运动;快速举升装备设置于船体上甲板,根据举升要求选择举升臂组队数目。单个举升臂系统结构如图2所示,局部坐标系与整体坐标系方向一致,其可根据作业需求调整其外沿臂长度,举升头和甲板支撑配备运动补偿系统,主要包含3种运动补偿模式:①举升臂可沿着x0方向的滑轨水平移动,从而补偿船体产生的纵荡运动;②举升臂可沿着y0方向的甲板支撑滑轨水平移动,从而补偿船体产生的横荡运动;③举升头可沿着z0方向垂向移动,从而补偿船体产生的垂荡运动。

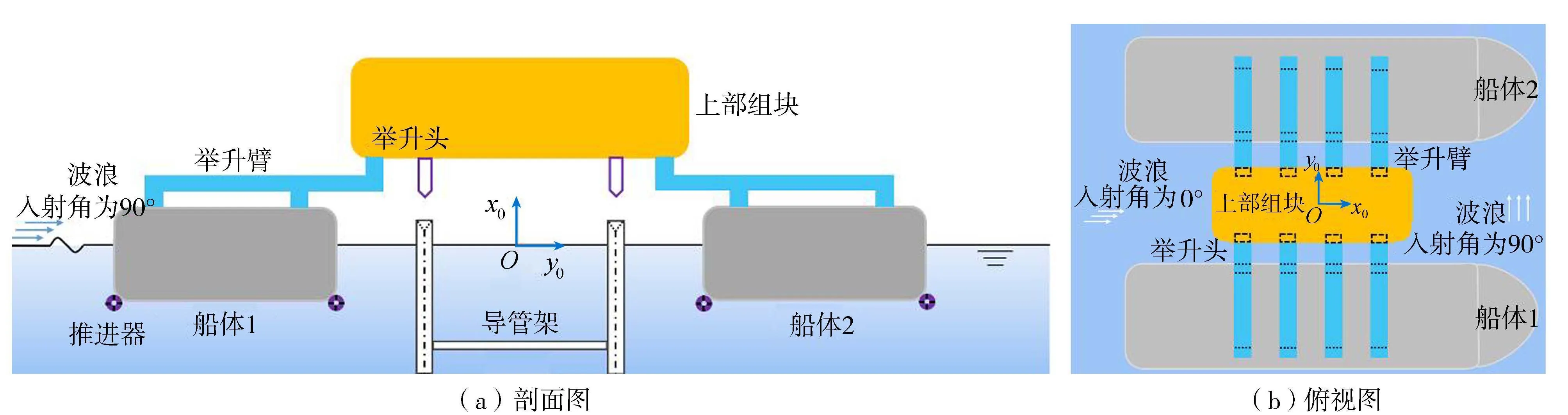
图1 双船联合举升多体协同作业系统示意图

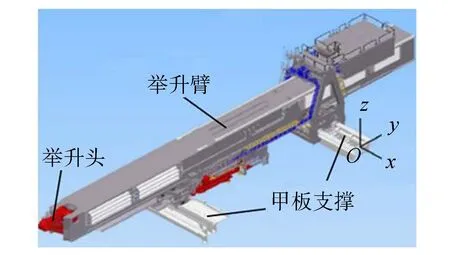
图2 举升臂系统结构

1.2 双船联合举升作业过程

双船联合举升作业过程主要步骤包括:①进船。双船体从两侧分别靠近导管架基础,就位后举升系统连接上部组块底部,此时上部组块全部重量仍位于导管架支撑上,运动补偿系统开始作业,减少举升臂和上部结构的碰撞;采用动力定位系统限制船体的水平位移。②压载荷载转移。通过排压载作业,将部分上部组块重量转移到双船体。③快速举升。在上部组块转移重量达到目标百分比后,快速举升系统开始作业,液压杆快速抬升,可实现基础与上部组块的快速分离;该过程系统稳性为本文关注重点。④退船。载有上部组块的双安装驳船,从基础结构正侧驶出。⑤荷载转移。采用压载系统和快速举升系统联合作业,完成上部组块从作业驳船到运输驳船的上部组块转移。⑥单船运输。为减少双船长距离运输作业风险,采用运输驳船,将上部组块运送到作业码头。

2 虚拟样机的建立与验证

本文主要采用虚拟样机方法对双船联合举升多体协同作业系统的横摇稳性进行研究。由于各机械结构和液压系统参数对该系统响应有较大影响,因而首先采用物理模型试验数据验证数值模型的准确性与可靠性,得到一致性结果后根据试验中船体运动响应,采用数值外推方法模拟系统多体横摇稳性规律;最后建立系统简化几何拓扑模型,实现系统横摇稳性的快速分析与预测。

2.1 多刚体系统动力学方程

举升作业船和上部组块的运动可认为是刚体的非线性运动,基于牛顿第二定律,重心的刚体动力学方程为

(1)

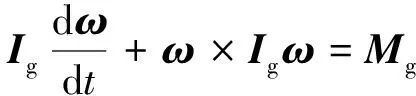
(2)

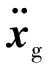
式(1)和式(2)仅适用于局部坐标系原点与重心重合的情况,更一般的动力学方程为

(3)

(4)

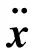
2.2 双船联合举升多体协同作业系统虚拟样机

基于ADAMS(automatic dynamic analysis of mechanical systems)平台建立描述双船协同举升过程中运动特征的虚拟样机,探讨船体运动和快速举升系统引起的上部组块的横摇稳性运动规律。实际作业船举升系统都配备运动补偿装置,通过液压驱动实现举升臂系统沿纵荡方向、横荡方向和垂荡方向的运动补偿,用以释放举升作业过程中多体耦合运动而产生的巨大载荷。本文基于原型及物理模型试验参数将运动补偿装置等效为横荡方向和垂荡方向弹簧阻尼系统,忽略纵荡方向运动补偿对系统横摇稳性的影响,整体系统虚拟样机如图3所示。

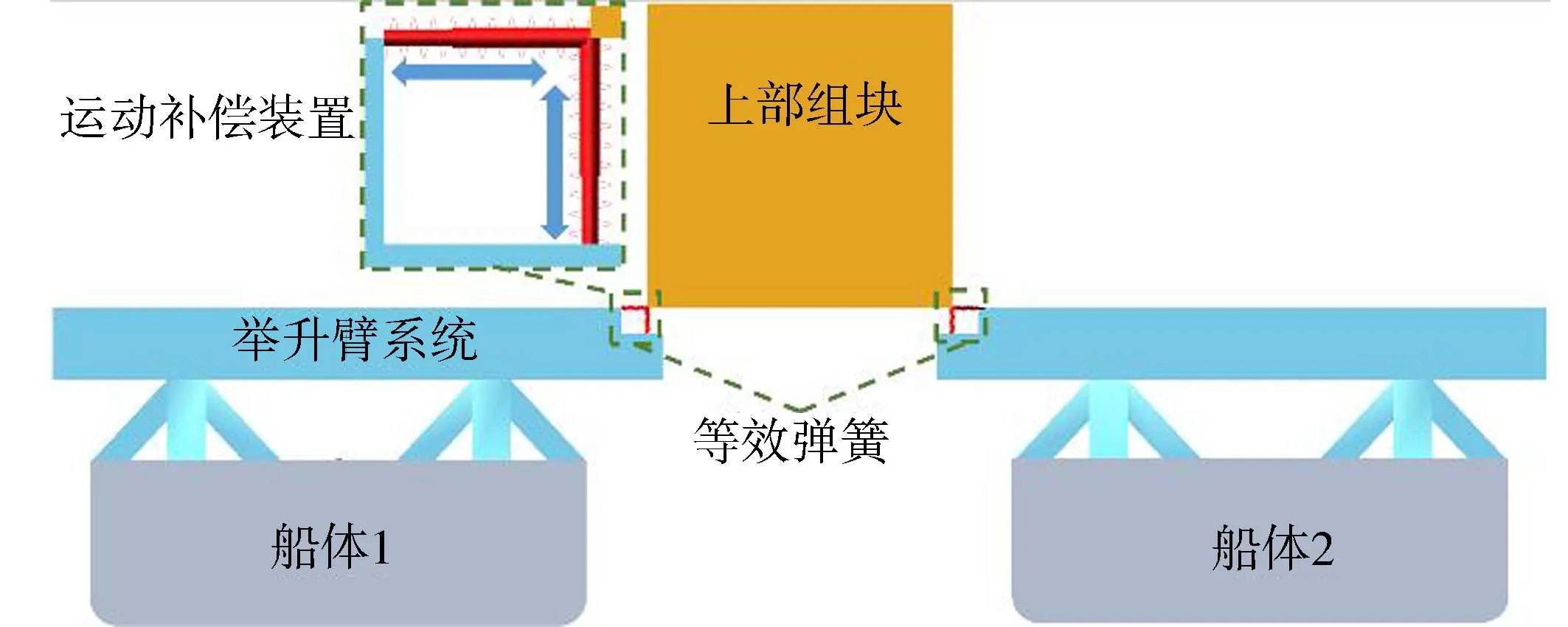
图3 双船联合举升多体协同作业系统虚拟样机

2.3 数值模拟试验验证

选用模型水池试验中3种典型作业海况进行横摇稳性研究。模型水池试验如图4所示,模型缩尺比为1∶50,该模型中每艘船配备了动力定位系统,使用弹簧和阻尼系统对举升臂的主动补偿系统进行等效简化,环境条件设置见表1。在水池试验中,波浪采用 JONSWAP海浪谱。选取海况Ⅰ和海况Ⅱ下的双船时域运动,将双船的垂荡和横摇运动作为虚拟样机的驱动,得到上部组块横摇运动的仿真数值,并与试验结果进行对比,如图5所示。表2对比了在海况Ⅰ和海况Ⅱ下试验和仿真得到的上部组块横摇幅值。

表1 模型试验的海况

图4 双船举升作业模型试验

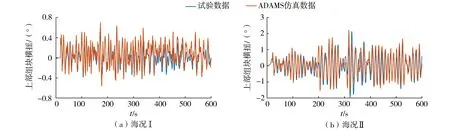
图5 上部组块横摇运动仿真结果与试验结果对比

由图5可见试验结果与仿真结果相吻合,说明本文建立的数值模型可实现上部组块横摇运动的准确仿真模拟。由表2可知,模型试验与数值仿真的结果存在一定误差,这是由于试验结果是2个船体在6个自由度真实耦合运动下的响应,而仿真结果是施加2个船体横摇和垂荡最危险组合运动驱动。

3 系统横摇稳性评估

双船与上部组块之间通过等效的弹簧阻尼连接形成了复杂的多体系统,在作业过程中,双船的相对独立运动增加了多体系统横摇稳态的不确定性。举升船与上部组块之间柔性连接,使得系统具有复杂的运动状态。通过建立系统横摇稳性的几何拓扑模型,可更容易描述双船与上部组块在耦合运动下的位置关系;并可由该模型推导上部组块的横摇角度计算公式,完成危险工况下系统横摇稳性的理论计算与仿真结果对比。

3.1 横摇稳性几何拓扑模型

以上部组块左倾状态为例,系统内多体之间位置关系如图6所示。图6中,O1为船1的重心,O2为船2的重心;A为船1与上部组块的连接点,B为船2与上部组块的连接点;r2为连接点到船体重心的水平距离,h2为连接点到船体中心的垂向距离;θ1为船1的横倾角,θ2为船2的横倾角,θ为上部组块的横倾角;Δh为双船之间的垂荡距离。

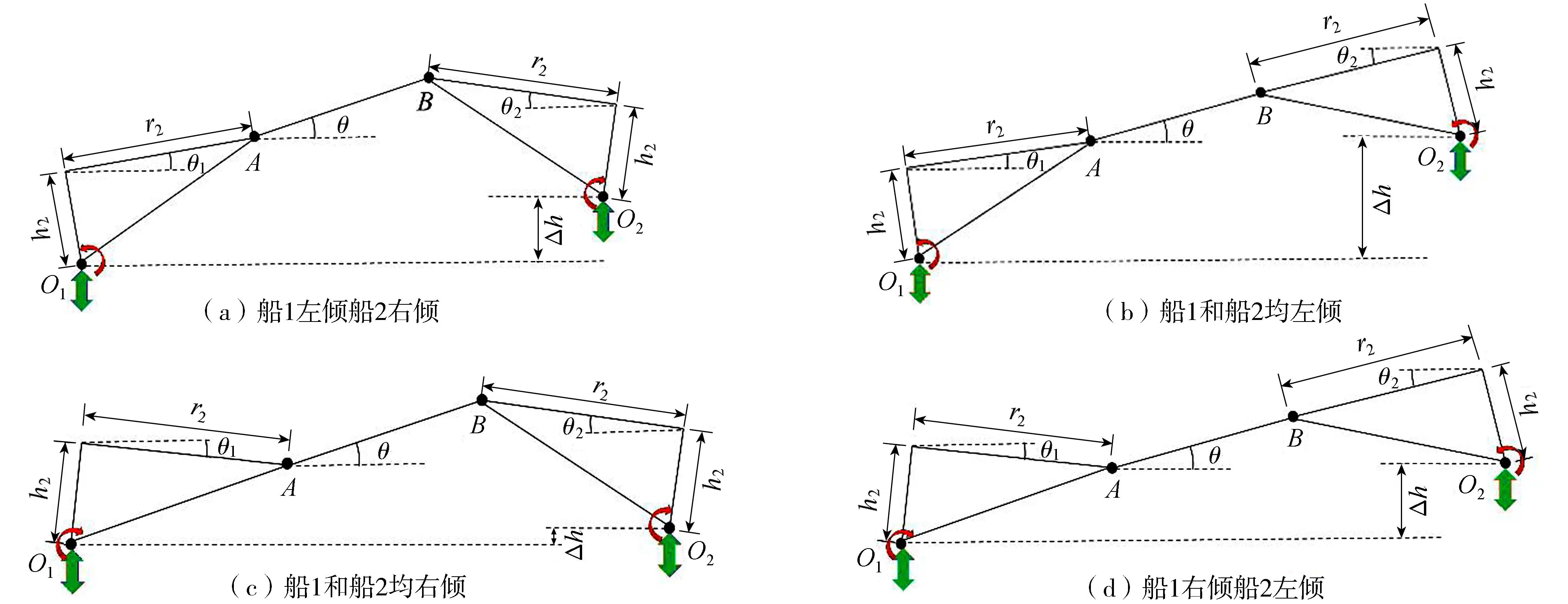
图6 上部组块与双船之间的位置关系

根据图6所示的4种情况,上部组块和双船的横摇角以及船2相对于船1的垂荡距离之间的关系可以表示为

h2cosθ1+r2sinθ1+2r1sinθ=Δh+r2sinθ2+h2cosθ2

(5)

h2cosθ1+r2sinθ1+2r1sinθ=Δh+h2cosθ2-r2sinθ2

(6)

h2cosθ1-r2sinθ1+2r1sinθ=Δh+r2sinθ2+h2cosθ2

(7)

h2cosθ1-r2sinθ1+2r1sinθ=Δh+h2cosθ2-r2sinθ2

(8)

在举升作业过程中,双船的相对运动导致上部组块产生横倾角θ。根据θ所处的不同区间,上部组块的状态可以分为图7所示的3种状态。图7中,O为上部组块的重心,r1为连接点到上部组块重心的水平距离,h1为上部组块重心到连接点连线AB的距离,FA为连接点A处的受力,FB为连接点B处的受力,mtg为上部组块的重力,la和lb为力臂,α为FB与AB之间的夹角,β为FA与AB之间的夹角。

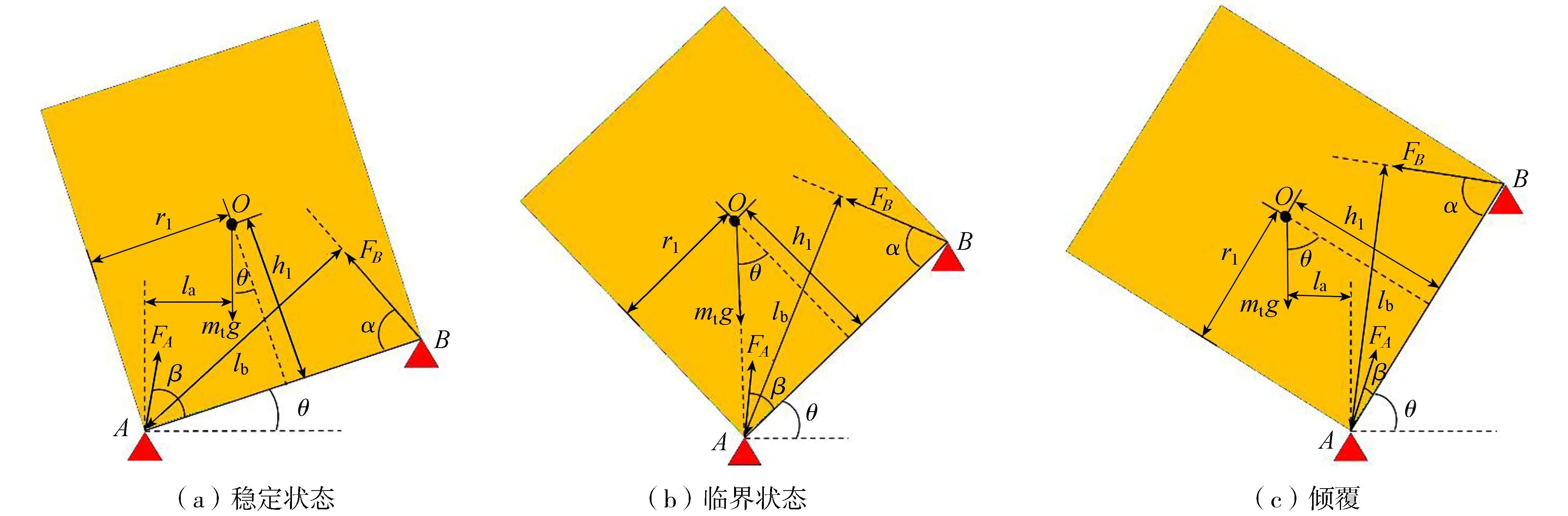
图7 不同横倾角时上部组块的状态

根据力矩平衡原理,给出力矩平衡方程:

∑MA=0

(9)

在该几何拓扑模型中,上部组块的重力与连接点B处的力的合力力矩等于0,所以

mtg(r1cosθ-h1sinθ)-FB2r1sinα=0

(10)

或者表示为

mtgla-FBlb=0

(11)

其中

la=r1cosθ-h1sinθlb=2r1sinα

当上部组块处于临界状态时,如图7(b)所示,力臂la=0;如果上部组块的横倾角度继续增加,则将发展为倾覆状态,如图7(c)所示,此时力臂la为

la=h1sinθ-r1cosθ

(12)

3.2 耦合运动参数化分析

将表1中海况Ⅲ条件下模型试验测得的双船时域运动响应作为驱动施加给虚拟样机,分析典型假设条件下上部组块横摇的耦合响应特性,表3给出了双船在不同运动特性下的5个仿真工况。

表3 仿真工况

由图8可知,双船的同相位横摇运动会使上部组块产生较大的横摇,横摇幅值为6.45°;而双船的反相位横摇运动对上部组块的影响很小。

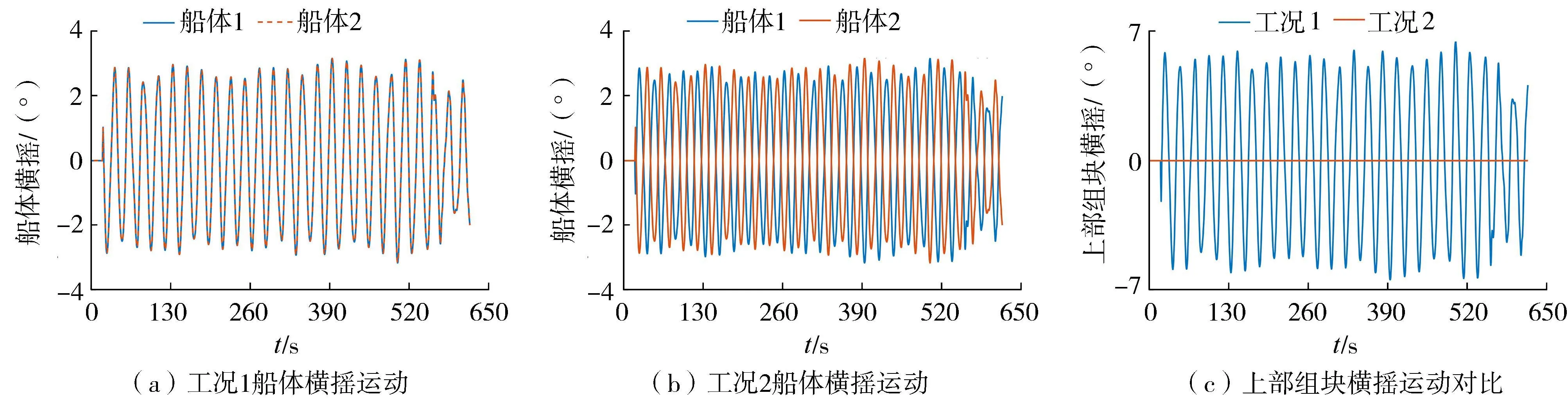
图8 工况1、工况2船体横摇运动与上部组块横摇运动时程曲线

由图9可知,双船的同相位垂荡运动对上部组块的横摇运动影响很小,而双船的反相位垂荡运动会使上部组块产生较大的横摇。

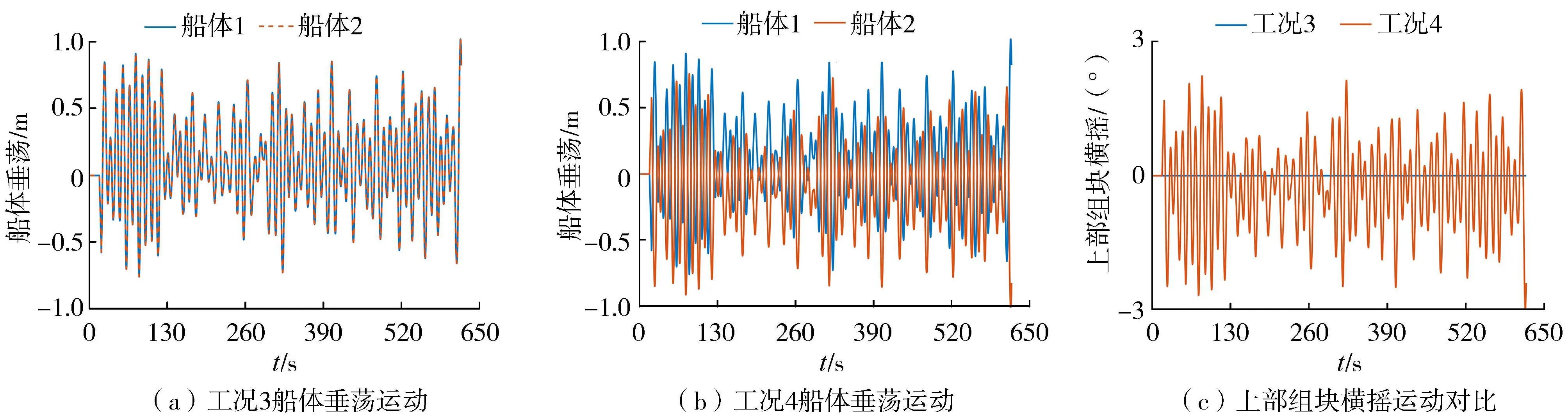
图9 工况3、工况4船体垂荡运动与上部组块横摇运动时程曲线

由图8(c)和图9(c)可知,工况1和工况4会使上部组块产生较大的横摇,这2种工况的组合工况(工况5)下上部组块的横摇运动时程曲线如图10所示,上部组块的横摇幅值为7.14°。双船同相位横摇和反相位垂荡耦合运动对上部组块的横摇运动影响最大,其中工况5双船同相位横摇和反相位垂荡耦合运动是上部组块发生横摇失稳的最危险工况。

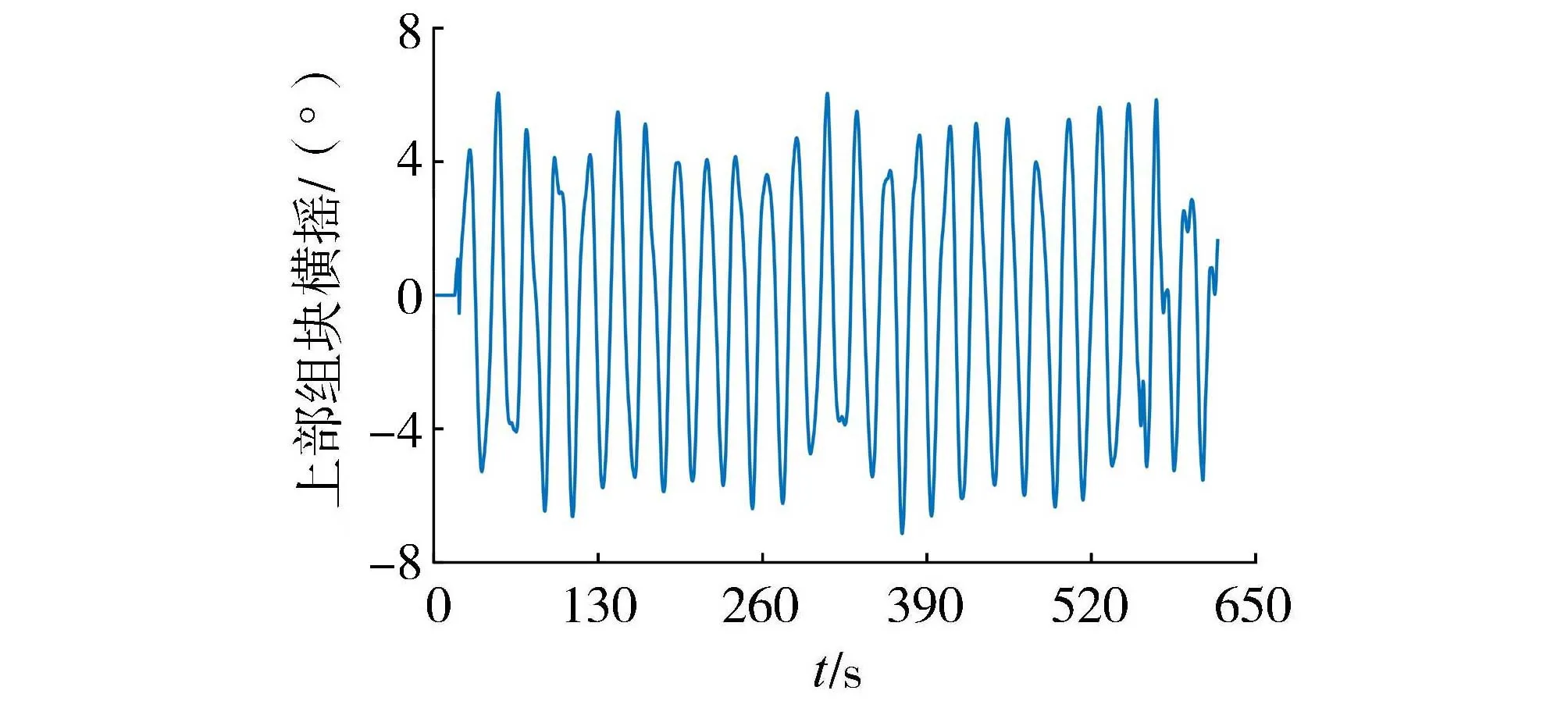
图10 工况5上部组块横摇运动时程曲线

3.3 横摇稳性与极限作业能力分析预测

基于参数化数值仿真模拟结果,选择最危险的工况5,改变h1/r1,通过ADAMS虚拟仿真得到上部组块不同的h1/r1值对应的最大横倾角(图11),并且对比本文建立的横摇稳性快速分析几何拓扑模型,探讨双船举升系统的极限作业能力。

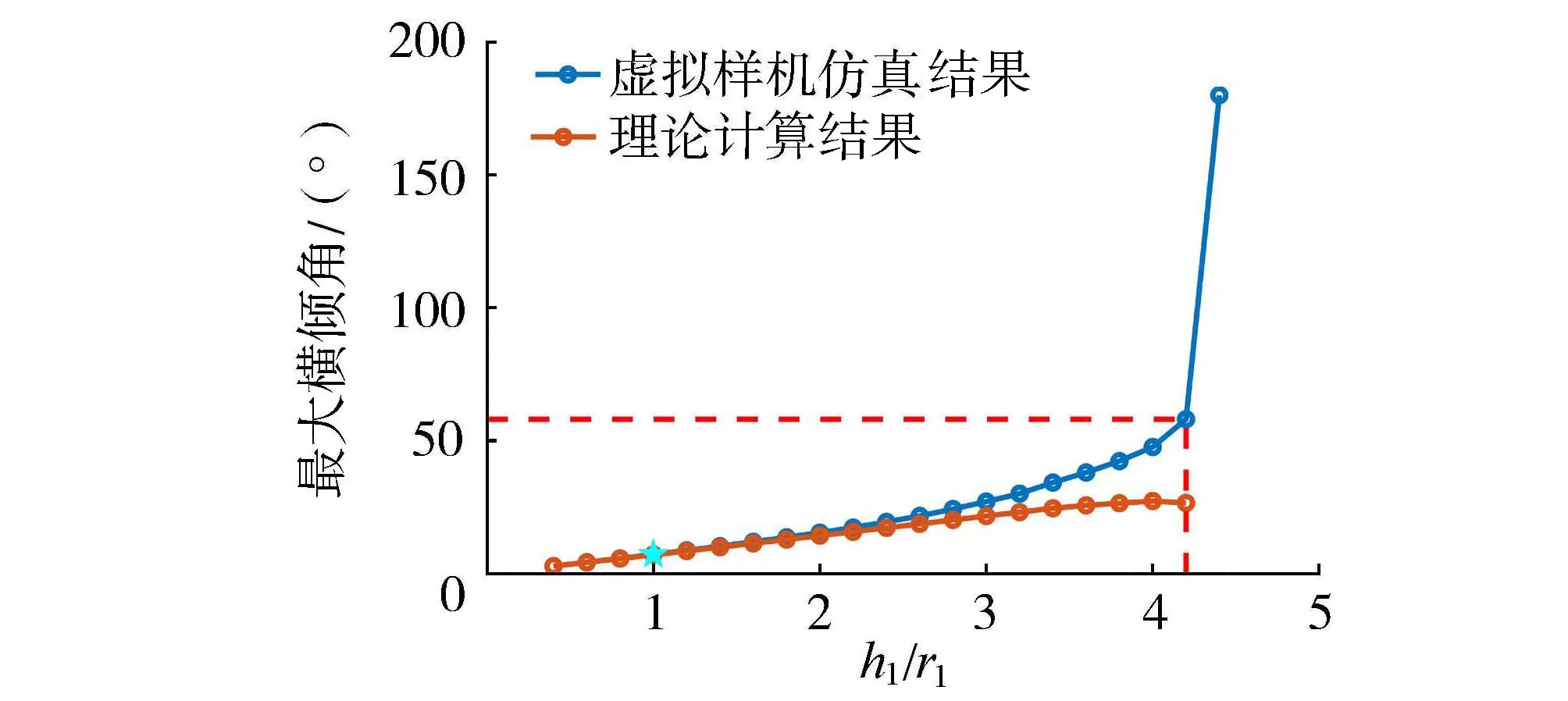
图11 上部组块最大横倾角仿真与理论数值

图11为ADAMS数值仿真结果和理论模型结果的对比,可见在一定范围内(h1/r1≤2),虚拟样机仿真结果与本文建立的几何拓扑模型实现上部组块最大横倾角的估计值规律一致。由于本文理论模型没有计入运动补偿系统的影响和系统的动态响应过程,在上部组块大纵横比情况下,理论模型低估了上部组块最大横倾角度。初始h1/r1的值为1时,上部组块的最大横倾角为7.23°;随着h1/r1的不断增大,上部组块的最大横倾角不断增大;当h1/r1>4.2时,上部组块会发生倾覆而失稳。

4 结 论

a.以物理模型试验和虚拟样机交叉驱动方式可以高效准确得到上部组块横摇运动的时域响应规律,验证举升系统中的主动补偿装置简化合理性。

b.双船的同相位横摇与反相位垂荡耦合运动对上部组块的横摇运动影响最大。

c.h1/r1一定范围内(h1/r1≤2)本文建立的几何拓扑模型可实现上部组块横倾角的准确估计。

d.上部组块横摇失稳时极限纵横比h1/r1可以作为多体系统横摇稳性评估参数。

e.由于本文理论模型没有计入运动补偿系统的影响和系统的动态响应过程,所以在上部组块纵横比较大的情况下,理论模型低估了上部组块横倾角度,需进一步修正完善。